Program to find Nth term divisible by a or b
Last Updated :
06 Apr, 2023
Given two integers 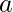 and
and 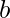 . The task is to find the Nth term which is divisible by either of
. The task is to find the Nth term which is divisible by either of 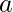 or
or 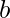 .
.
Examples :
Input : a = 2, b = 5, N = 10
Output : 16
Input : a = 3, b = 7, N = 25
Output : 57
Naive Approach: A simple approach is to traverse over all the terms starting from 1 until we find the desired Nth term which is divisible by either of 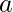 or
or 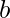 . This solution has time complexity of O(N).
. This solution has time complexity of O(N).
C++
#include <bits/stdc++.h>
using namespace std;
int findNthTerm(int A, int B, int n)
{
long i = min(A, B);
for (; n; i++)
if (i % A == 0 || i % B == 0)
n--;
return (i - 1);
}
int main()
{
int a = 2, b = 5, n = 10;
cout << findNthTerm(a, b, n) << endl;
return 0;
}
|
Java
import java.util.*;
class Main {
static int findNthTerm(int A, int B, int n) {
long i = Math.min(A, B);
for (; n > 0; i++) {
if (i % A == 0 || i % B == 0) {
n--;
}
}
return (int) (i - 1);
}
public static void main(String[] args) {
int a = 2, b = 5, n = 10;
System.out.println(findNthTerm(a, b, n));
}
}
|
Python3
def findNthTerm(A, B, n):
i = min(A, B)
while n > 0:
if i % A == 0 or i % B == 0:
n -= 1
i += 1
return i - 1
a = 2
b = 5
n = 10
print(findNthTerm(a, b, n))
|
Javascript
function findNthTerm(A, B, n) {
let i = Math.min(A, B);
while (n) {
if (i % A === 0 || i % B === 0) {
n--;
}
i++;
}
return i - 1;
}
const a = 2,
b = 5,
n = 10;
console.log(findNthTerm(a, b, n));
|
C#
using System;
public class GFG {
static int findNthTerm(int A, int B, int n)
{
long i = Math.Min(A, B);
for (; n > 0; i++)
if (i % A == 0 || i % B == 0)
n--;
return (int)(i - 1);
}
public static void Main()
{
int a = 2, b = 5, n = 10;
Console.WriteLine(findNthTerm(a, b, n));
}
}
|
Output:
16
Time complexity: O(N), as traversing over the terms.
Space complexity: O(1), as constanst space is used.
Efficient Approach:
Intuition:
How to use Binary Search for this problem?
Determining the Binary Search Condition:
First, we need to identify the condition for our binary search, magicNumbersLessEqual(x). Given a number x, the count of numbers <= x that are divisible by A is given by ?x/A?. For example, if x = 17 and A = 3, then ?x/A? = 5. Similarly, the count of numbers <= x that are divisible by B is ?x/B?.
However, we cannot simply use ?x/A? + ?x/B? as the total count of numbers less than x that are divisible by A or B, as we might be double counting numbers that are divisible by both A and B. To account for this, we need to subtract the count of numbers that are divisible by both A and B, which are the LCM and its multiples. The count of numbers <= x that are multiples of LCM(A,B) will be ?x/LCM?. So, the final function becomes magicNumbersLessEqual(x) = ?x/A? + ?x/B? – ?x/LCM?.
Range of Binary Search:
Next, we need to determine the range of our search space. The starting point, L, is the minimum of A and B, as no number lower than that would be divisible by either. The end point, R, is N * min(A,B), as this will ensure that there are at least N magical numbers.
During each iteration, we calculate the midpoint and determine magicNumbersLessEqual(mid). If it is less than N, we set L = mid + 1 as any number less than mid cannot be the answer. If it is greater than N, we set R = mid – 1 as any number greater than mid cannot be the answer. Finally, we return the number that gives us N magical numbers <= it, which will be the Nth magical number.
The idea is to use Binary search. Here we can calculate how many numbers from 1 to 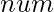 are divisible by either a or b by using formula:
are divisible by either a or b by using formula:
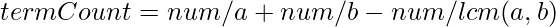
All the multiples of lcm(a, b) will be divisible by both 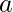 and
and 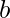 so we need to remove these terms. Now if the number of divisible terms is less than N we will increase the low position of binary search otherwise decrease high until number of divisible terms is equal to N.
so we need to remove these terms. Now if the number of divisible terms is less than N we will increase the low position of binary search otherwise decrease high until number of divisible terms is equal to N.
Below is the implementation of the above idea :
C++
#include <bits/stdc++.h>
using namespace std;
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
int divTermCount(int a, int b, int lcm, int num)
{
return num / a + num / b - num / lcm;
}
int findNthTerm(int a, int b, int n)
{
int low = 1, high = min(a, b) * n , mid;
int lcm = (a * b) / gcd(a, b);
while (low < high) {
mid = low + (high - low) / 2;
if (divTermCount(a, b, lcm, mid) < n)
low = mid + 1;
else
high = mid;
}
return low;
}
int main()
{
int a = 2, b = 5, n = 10;
cout << findNthTerm(a, b, n) << endl;
return 0;
}
|
Java
class GFG
{
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
static int divTermCount(int a, int b,
int lcm, int num)
{
return num / a + num / b - num / lcm;
}
static int findNthTerm(int a, int b, int n)
{
int low = 1, high = Integer.MAX_VALUE, mid;
int lcm = (a * b) / gcd(a, b);
while (low < high)
{
mid = low + (high - low) / 2;
if (divTermCount(a, b, lcm, mid) < n)
low = mid + 1;
else
high = mid;
}
return low;
}
public static void main (String[] args)
{
int a = 2, b = 5, n = 10;
System.out.println(findNthTerm(a, b, n));
}
}
|
Python3
import sys
def gcd(a, b):
if a == 0:
return b
return gcd(b % a, a)
def divTermCount(a, b, lcm, num):
return num // a + num // b - num // lcm
def findNthTerm(a, b, n):
low = 1; high = sys.maxsize
lcm = (a * b) // gcd(a, b)
while low < high:
mid = low + (high - low) // 2
if divTermCount(a, b, lcm, mid) < n:
low = mid + 1
else:
high = mid
return low
a = 2; b = 5; n = 10
print(findNthTerm(a, b, n))
|
C#
using System;
class GFG
{
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
static int divTermCount(int a, int b,
int lcm, int num)
{
return num / a + num / b - num / lcm;
}
static int findNthTerm(int a, int b, int n)
{
int low = 1, high = int.MaxValue, mid;
int lcm = (a * b) / gcd(a, b);
while (low < high)
{
mid = low + (high - low) / 2;
if (divTermCount(a, b, lcm, mid) < n)
low = mid + 1;
else
high = mid;
}
return low;
}
static public void Main ()
{
int a = 2, b = 5, n = 10;
Console.WriteLine(findNthTerm(a, b, n));
}
}
|
Javascript
<script>
function gcd(a , b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
function divTermCount(a , b, lcm , num)
{
return parseInt(num / a) +
parseInt(num / b) - parseInt(num / lcm);
}
function findNthTerm(a , b , n)
{
var low = 1, high = Number.MAX_VALUE, mid;
var lcm = parseInt((a * b) / gcd(a, b));
while (low < high)
{
mid = low + parseInt((high - low) / 2);
if (divTermCount(a, b, lcm, mid) < n)
low = mid + 1;
else
high = mid;
}
return low;
}
var a = 2, b = 5, n = 10;
document.write(findNthTerm(a, b, n));
</script>
|
There is a third approach that takes O(log(min(a, b))).
Worst Case Time Complexity – O(log(min(a, b)))
Auxiliary Space: O(1)
C++
#include <bits/stdc++.h>
using namespace std;
long long gcd(long long a, long long b)
{
long long temp = a + b;
a = (a > b) ? a : b;
b = temp - a;
if (a % b == 0) {
return b;
}
return gcd(b, a % b);
}
long long trUE_n_Smallest_AB(long long a, long long b,
long long n)
{
if (n * a < b) {
return n * a;
}
if (n * a == b) {
return a * (n + 1);
}
long long g = gcd(a, b);
a /= g;
b /= g;
long long filler = 0;
long long sum = 0;
if (n > a + b - 2) {
sum = a + b - 2;
filler = (n / sum) * a * b;
n %= sum;
}
if (n == 0) {
return g * (filler - a);
}
long long rat_a = (n * b) / (a + b);
long long rat_b = (n * a) / (a + b);
if (a * rat_a > b * rat_b) {
return g
* (min(a * rat_a + a, b * rat_b + b)
+ filler);
}
else {
return g * (a * rat_a + a + filler);
}
}
long long boTH_trUE_n_Smallest_AB(long long a, long long b,
long long n)
{
if (n * a <= b) {
return n * a;
}
long long g = gcd(a, b);
a /= g;
b /= g;
long long filler = 0;
long long sum = 0;
if (n > a + b - 1) {
sum = a + b - 1;
filler = (n / sum) * a * b;
n %= sum;
}
if (n == 0) {
return g * (filler - a);
}
long long rat_a = (n * b) / (a + b);
long long rat_b = (n * a) / (a + b);
if (a * rat_a > b * rat_b) {
return g
* (min(a * rat_a + a, b * rat_b + b)
+ filler);
}
else {
return g * (a * rat_a + a + filler);
}
}
int main(void)
{
long long a = 2, b = 5, n = 10;
long long true_a = min(a, b);
long long true_b = max(a, b);
long long answer
= boTH_trUE_n_Smallest_AB(true_a, true_b, n);
cout << answer << endl;
return 0;
}
|
C
#include <stdio.h>
long long min(long long a, long long b)
{
return (a < b) ? a : b;
}
long long max(long long a, long long b)
{
return (a > b) ? a : b;
}
long long gcd(long long a, long long b)
{
long long temp = a + b;
a = (a > b) ? a : b;
b = temp - a;
if (a % b == 0) {
return b;
}
return gcd(b, a % b);
}
long long trUE_n_Smallest_AB(long long a, long long b,
long long n)
{
if (n * a < b) {
return n * a;
}
if (n * a == b) {
return a * (n + 1);
}
long long g = gcd(a, b);
a /= g;
b /= g;
long long filler = 0;
long long sum = 0;
if (n > a + b - 2) {
sum = a + b - 2;
filler = (n / sum) * a * b;
n %= sum;
}
if (n == 0) {
return g * (filler - a);
}
long long rat_a = (n * b) / (a + b);
long long rat_b = (n * a) / (a + b);
if (a * rat_a > b * rat_b) {
return g
* (min(a * rat_a + a, b * rat_b + b)
+ filler);
}
else {
return g * (a * rat_a + a + filler);
}
}
long long boTH_trUE_n_Smallest_AB(long long a, long long b,
long long n)
{
if (n * a <= b) {
return n * a;
}
long long g = gcd(a, b);
a /= g;
b /= g;
long long filler = 0;
long long sum = 0;
if (n > a + b - 1) {
sum = a + b - 1;
filler = (n / sum) * a * b;
n %= sum;
}
if (n == 0) {
return g * (filler - a);
}
long long rat_a = (n * b) / (a + b);
long long rat_b = (n * a) / (a + b);
if (a * rat_a > b * rat_b) {
return g
* (min(a * rat_a + a, b * rat_b + b)
+ filler);
}
else {
return g * (a * rat_a + a + filler);
}
}
int main(void)
{
long long a = 2, b = 5, n = 10;
long long true_a = min(a, b);
long long true_b = max(a, b);
long long answer
= boTH_trUE_n_Smallest_AB(true_a, true_b, n);
printf("%lli\n", answer);
return 0;
}
|
Java
import java.io.*;
class GFG {
public static long gcd(long a, long b)
{
long temp = a + b;
a = (a > b) ? a : b;
b = temp - a;
if (a % b == 0) {
return b;
}
return gcd(b, a % b);
}
public static long trUE_n_Smallest_AB(long a, long b,
long n)
{
if (n * a < b) {
return n * a;
}
if (n * a == b) {
return a * (n + 1);
}
long g = gcd(a, b);
a /= g;
b /= g;
long filler = 0;
long sum = 0;
if (n > a + b - 2) {
sum = a + b - 2;
filler = (n / sum) * a * b;
n %= sum;
}
if (n == 0) {
return g * (filler - a);
}
long rat_a = (n * b) / (a + b);
long rat_b = (n * a) / (a + b);
if (a * rat_a > b * rat_b) {
return g
* (Math.min(a * rat_a + a, b * rat_b + b)
+ filler);
}
else {
return g * (a * rat_a + a + filler);
}
}
public static long
boTH_trUE_n_Smallest_AB(long a, long b, long n)
{
if (n * a <= b) {
return n * a;
}
long g = gcd(a, b);
a /= g;
b /= g;
long filler = 0;
long sum = 0;
if (n > a + b - 1) {
sum = a + b - 1;
filler = (n / sum) * a * b;
n %= sum;
}
if (n == 0) {
return g * (filler - a);
}
long rat_a = (n * b) / (a + b);
long rat_b = (n * a) / (a + b);
if (a * rat_a > b * rat_b) {
return g
* (Math.min(a * rat_a + a, b * rat_b + b)
+ filler);
}
else {
return g * (a * rat_a + a + filler);
}
}
public static void main(String[] args)
{
long a = 2, b = 5, n = 10;
long true_a = Math.min(a, b);
long true_b = Math.max(a, b);
long answer
= boTH_trUE_n_Smallest_AB(true_a, true_b, n);
System.out.println(answer);
}
}
|
Python3
def gcd(a, b):
temp = a+b
if (a < b):
a = b
b = temp - a
if (a % b == 0):
return b
return gcd(b, a % b)
def trUE_n_Smallest_AB(a, b, n):
if (n*a < b):
return n*a
if (n*a == b):
return a*(n+1)
g = gcd(a, b)
a //= g
b //= g
filler = 0
sum = 0
if (n > a+b-2):
sum = a + b - 2
filler = (n//sum)*a*b
n %= sum
if (n == 0):
return g*(filler - a)
rat_a = (n*b)//(a+b)
rat_b = (n*a)//(a+b)
if(a*rat_a > b*rat_b):
return g*(min(a*rat_a+a, b*rat_b + b) + filler)
else:
return g*(a*rat_a + a + filler)
def boTH_trUE_n_Smallest_AB(a, b, n):
if (n*a <= b):
return n*a
g = gcd(a, b)
a //= g
b //= g
filler = 0
sum = 0
if (n > a+b - 1):
sum = a + b - 1
filler = (n//sum)*a*b
n %= sum
if (n == 0):
return g*(filler - a)
rat_a = (n*b)//(a+b)
rat_b = (n*a)//(a+b)
if(a*rat_a > b*rat_b):
return g*(min(a*rat_a+a, b*rat_b + b) + filler)
else:
return g*(a*rat_a + a + filler)
a = 2
b = 5
n = 10
true_a = min(a, b)
true_b = max(a, b)
answer = boTH_trUE_n_Smallest_AB(true_a, true_b, n)
print(answer)
|
C#
using System;
public class Gfg {
public static long gcd(long a, long b)
{
long temp = a + b;
a = (a > b) ? a : b;
b = temp - a;
if (a % b == 0) {
return b;
}
return gcd(b, a % b);
}
public static long trUE_n_Smallest_AB(long a, long b,
long n)
{
if (n * a < b) {
return n * a;
}
if (n * a == b) {
return a * (n + 1);
}
long g = gcd(a, b);
a /= g;
b /= g;
long filler = 0;
long sum = 0;
if (n > a + b - 2) {
sum = a + b - 2;
filler = (n / sum) * a * b;
n %= sum;
}
if (n == 0) {
return g * (filler - a);
}
long rat_a = (n * b) / (a + b);
long rat_b = (n * a) / (a + b);
if (a * rat_a > b * rat_b) {
return g
* (Math.Min(a * rat_a + a, b * rat_b + b)
+ filler);
}
else {
return g * (a * rat_a + a + filler);
}
}
public static long
boTH_trUE_n_Smallest_AB(long a, long b, long n)
{
if (n * a <= b) {
return n * a;
}
long g = gcd(a, b);
a /= g;
b /= g;
long filler = 0;
long sum = 0;
if (n > a + b - 1) {
sum = a + b - 1;
filler = (n / sum) * a * b;
n %= sum;
}
if (n == 0) {
return g * (filler - a);
}
long rat_a = (n * b) / (a + b);
long rat_b = (n * a) / (a + b);
if (a * rat_a > b * rat_b) {
return g
* (Math.Min(a * rat_a + a, b * rat_b + b)
+ filler);
}
else {
return g * (a * rat_a + a + filler);
}
}
public static void Main()
{
long a = 2, b = 5, n = 10;
long true_a = Math.Min(a, b);
long true_b = Math.Max(a, b);
long answer
= boTH_trUE_n_Smallest_AB(true_a, true_b, n);
Console.WriteLine(answer);
}
}
|
Javascript
function gcd(a, b) {
let temp = a + b;
a = (a > b) ? a : b;
b = temp - a;
if (a % b === 0) {
return b;
}
return gcd(b, a % b);
}
function trUE_n_Smallest_AB(a, b, n) {
if (n * a < b) {
return n * a;
}
if (n * a === b) {
return a * (n + 1);
}
let g = gcd(a, b);
a /= g;
b /= g;
let filler = 0;
let sum = 0;
if (n > a + b - 2) {
sum = a + b - 2;
filler = Math.floor(n / sum) * a * b;
n %= sum;
}
if (n === 0) {
return g * (filler - a);
}
let rat_a = Math.floor((n * b) / (a + b));
let rat_b = Math.floor((n * a) / (a + b));
if (a * rat_a > b * rat_b) {
return g * (Math.min(a * rat_a + a, b * rat_b + b) + filler);
} else {
return g * (a * rat_a + a + filler);
}
}
function boTH_trUE_n_Smallest_AB(a, b, n) {
if (n * a <= b) {
return n * a;
}
let g = gcd(a, b);
a /= g;
b /= g;
let filler = 0;
let sum = 0;
if (n > a + b - 1) {
sum = a + b - 1;
filler = Math.floor(n / sum) * a * b;
n %= sum;
}
if (n === 0) {
return g * (filler - a);
}
let rat_a = Math.floor((n * b) / (a + b));
let rat_b = Math.floor((n * a) / (a + b));
if (a * rat_a > b * rat_b) {
return g * (Math.min(a * rat_a + a, b * rat_b + b) + filler);
} else {
return g * (a * rat_a + a + filler);
}
}
let a = 2, b = 5, n = 10;
let true_a = Math.min(a, b);
let true_b = Math.max(a, b);
let answer = boTH_trUE_n_Smallest_AB(true_a, true_b, n);
console.log(answer);
|
This approach uses density of a and b, and solves for n.
The approach takes only O(log(min(a, b))) time as only simple mathematical operations(add, subtract, multiply and divide, minimum/maximum of 2 numbers -> all O(1) and gcd operation-> O(log(min(a, b)))) are used here.
NOTE ON Modulo(“%”): a-=b*(a/b) is equivalent to a%=b, so you can assume that to be O(1) as well.
Share your thoughts in the comments
Please Login to comment...