Linear Search Algorithm – Data Structure and Algorithms Tutorials
Last Updated :
18 Mar, 2024
Linear Search is defined as a sequential search algorithm that starts at one end and goes through each element of a list until the desired element is found, otherwise the search continues till the end of the data set.
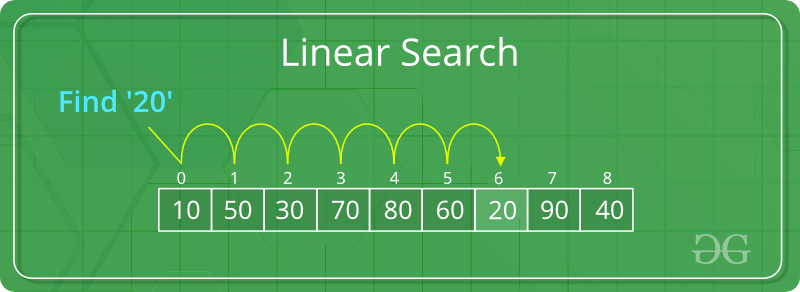
Linear Search Algorithm
How Does Linear Search Algorithm Work?
In Linear Search Algorithm,
- Every element is considered as a potential match for the key and checked for the same.
- If any element is found equal to the key, the search is successful and the index of that element is returned.
- If no element is found equal to the key, the search yields “No match found”.
For example: Consider the array arr[] = {10, 50, 30, 70, 80, 20, 90, 40} and key = 30
Step 1: Start from the first element (index 0) and compare key with each element (arr[i]).
- Comparing key with first element arr[0]. SInce not equal, the iterator moves to the next element as a potential match.
![Compare key with arr[0]](https://media.geeksforgeeks.org/wp-content/uploads/20230519161339/Linear-search-algorithm-1.webp)
Compare key with arr[0]
- Comparing key with next element arr[1]. SInce not equal, the iterator moves to the next element as a potential match.
![Compare key with arr[1]](https://media.geeksforgeeks.org/wp-content/uploads/20230519161415/Linear-search-algorithm-2.webp)
Compare key with arr[1]
Step 2: Now when comparing arr[2] with key, the value matches. So the Linear Search Algorithm will yield a successful message and return the index of the element when key is found (here 2).
![Compare key with arr[2]](https://media.geeksforgeeks.org/wp-content/uploads/20230519161442/Linear-search-algorithm-3.webp)
Compare key with arr[2]
Implementation of Linear Search Algorithm:
Below is the implementation of the linear search algorithm:
C++
// C++ code to linearly search x in arr[].
#include <bits/stdc++.h>
using namespace std;
int search(int arr[], int N, int x)
{
for (int i = 0; i < N; i++)
if (arr[i] == x)
return i;
return -1;
}
// Driver code
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int N = sizeof(arr) / sizeof(arr[0]);
// Function call
int result = search(arr, N, x);
(result == -1)
? cout << "Element is not present in array"
: cout << "Element is present at index " << result;
return 0;
}
// C code to linearly search x in arr[].
#include <stdio.h>
int search(int arr[], int N, int x)
{
for (int i = 0; i < N; i++)
if (arr[i] == x)
return i;
return -1;
}
// Driver code
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int N = sizeof(arr) / sizeof(arr[0]);
// Function call
int result = search(arr, N, x);
(result == -1)
? printf("Element is not present in array")
: printf("Element is present at index %d", result);
return 0;
}
// Java code for linearly searching x in arr[].
import java.io.*;
class GFG {
public static int search(int arr[], int N, int x)
{
for (int i = 0; i < N; i++) {
if (arr[i] == x)
return i;
}
return -1;
}
// Driver code
public static void main(String args[])
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
// Function call
int result = search(arr, arr.length, x);
if (result == -1)
System.out.print(
"Element is not present in array");
else
System.out.print("Element is present at index "
+ result);
}
}
// C# code to linearly search x in arr[].
using System;
class GFG {
public static int search(int[] arr, int N, int x)
{
for (int i = 0; i < N; i++) {
if (arr[i] == x)
return i;
}
return -1;
}
// Driver's code
public static void Main()
{
int[] arr = { 2, 3, 4, 10, 40 };
int x = 10;
// Function call
int result = search(arr, arr.Length, x);
if (result == -1)
Console.WriteLine(
"Element is not present in array");
else
Console.WriteLine("Element is present at index "
+ result);
}
}
// This code is contributed by DrRoot_
// Javascript code to linearly search x in arr[].
function search(arr, n, x)
{
for (let i = 0; i < n; i++)
if (arr[i] == x)
return i;
return -1;
}
// Driver code
let arr = [ 2, 3, 4, 10, 40 ];
let x = 10;
let n = arr.length;
// Function call
let result = search(arr, n, x);
(result == -1)
? console.log("Element is not present in array")
: console.log("Element is present at index " + result);
// This code is contributed by Manoj
<?php
// PHP code for linearly search x in arr[].
function search($arr, $n, $x)
{
for($i = 0; $i < $n; $i++) {
if($arr[$i] == $x)
return $i;
}
return -1;
}
// Driver Code
$arr = array(2, 3, 4, 10, 40);
$x = 10;
// Function call
$result = search($arr, sizeof($arr), $x);
if($result == -1)
echo "Element is not present in array";
else
echo "Element is present at index " ,
$result;
// This code is contributed
// by jit_t
?>
# Python3 code to linearly search x in arr[].
def search(arr, N, x):
for i in range(0, N):
if (arr[i] == x):
return i
return -1
# Driver Code
if __name__ == "__main__":
arr = [2, 3, 4, 10, 40]
x = 10
N = len(arr)
# Function call
result = search(arr, N, x)
if(result == -1):
print("Element is not present in array")
else:
print("Element is present at index", result)
OutputElement is present at index 3
Time Complexity:
- Best Case: In the best case, the key might be present at the first index. So the best case complexity is O(1)
- Worst Case: In the worst case, the key might be present at the last index i.e., opposite to the end from which the search has started in the list. So the worst-case complexity is O(N) where N is the size of the list.
- Average Case: O(N)
Auxiliary Space: O(1) as except for the variable to iterate through the list, no other variable is used.
Advantages of Linear Search:
- Linear search can be used irrespective of whether the array is sorted or not. It can be used on arrays of any data type.
- Does not require any additional memory.
- It is a well-suited algorithm for small datasets.
Drawbacks of Linear Search:
- Linear search has a time complexity of O(N), which in turn makes it slow for large datasets.
- Not suitable for large arrays.
When to use Linear Search?
- When we are dealing with a small dataset.
- When you are searching for a dataset stored in contiguous memory.
Share your thoughts in the comments
Please Login to comment...