Nonhomogeneous Poisson Processes

Non-homogeneous Poisson process model (NHPP) represents the number of failures experienced up to time t is a non-homogeneous Poisson process {N(t), t ≥ 0}.

The main issue in the NHPP model is to determine an appropriate mean value function to denote the expected number of failures experienced up to a certain time.
With different assumptions, the model will end up with different functional forms of the mean value function. Note that in a renewal process, the exponential assumption for the inter-arrival time between failures is relaxed, and in the NHPP, the stationary assumption is relaxed.

Non-homogeneous Poisson process model is based on the following assumptions:

–>The failure process has an independent increment, i.e. the number of failures during the time interval (t, t + s) depends on the current time t and the length of time interval s, and does not depend on the past history of the process.

–> The failure rate of the process is given by P{exactly one failure in (t, t + ∆t)} = P{N(t, t + ∆t) – N(t)=1} = 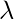(t)∆t + o(∆t) where 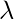(t) is the intensity function.

–> During a small interval ∆t, the probability of more than one failure is negligible, that is, P{two or more failure in (t, t+∆t)} = o(∆t)

–> The initial condition is N(0) = 0.

On the basis of these assumptions, the probability of exactly n failures occurring during the time interval (0, t) for the NHPP is given by
              

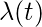
where    and   is the intensity function. It can be easily shown that the mean value function m(t) is non-decreasing.

Reliability Function:
The reliability R(t), defined as the probability that there are no failures in the time interval (0, t), is given by
              

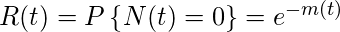
In general, the reliability R(x|t), the probability that there are no failures in the interval (t, t + x), is given by

              

and its density is given by
              
where

The variance of the NHPP can be obtained as follows: