Homogeneous Poisson Process
Last Updated :
29 Dec, 2021
The poisson process is one of the most important and widely used processes in probability theory. It is widely used to model random points in time or space. In this article we will discuss briefly about homogeneous Poisson Process.
Poisson Process –
Here we are deriving Poisson Process as a counting process. Let us assume that we are observing number of occurrence of certain event over a specified period of time. ( Here we are considering time as an example. We might also consider space etc.)We can consider them as happening under a Poisson Process provided they satisfy below conditions.
- The number of occurrences during disjoint time intervals are independent.
- The probability of a single occurrence during a small time interval is proportional to the length of the interval.
- The probability of more than one occurrence during a small time interval can be neglected.
If we denote number of occurrences during a time interval of length t as X(t) then
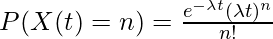
Examples –
Many real life situations can be modelled using Poisson Process. Suppose we consider number of accidents in a road. We can easily understand that the three above conditions are satisfied. For two disjoint time intervals number of accidents in a given road are independent, Again it is quite improbable that two or more accidents occur at a small interval of time. Intuitively we can also assume that probability that an accident occurs during a small interval of time is proportional to the length of the time interval. Number of earthquakes in a place can also be modelled using Poisson process.
Derivation –
Now we prove our claim that if X(t) be the number of occurrence in an interval of length t, then
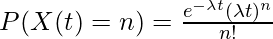
where 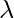 is the rate of occurrence.
is the rate of occurrence.
We will use mathematical induction to prove the statement. First we write the assumptions written above in mathematical terms. According to assumption 3 in a small time interval h
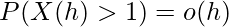
where 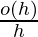 tends to zero as h tends to zero or
tends to zero as h tends to zero or
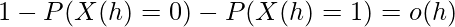 .
.
Again if 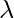 be the rate of occurrence then according to assumption 2 we get,
be the rate of occurrence then according to assumption 2 we get,
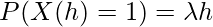 .
.
Let us take an interval (0, t) and a small interval (t, t+h). We will denote P(X(t)=n) as 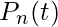 . So the above equations can be written as,
. So the above equations can be written as,
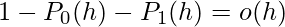
or
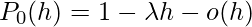
So we have to prove that
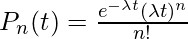 .
.
First we will prove the result for n=0 and n=1. Then we will show that if the result is true for n=m then it will be true for n=m+1.
Take the interval (0, t+h). Now,
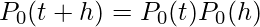
(since the occurrences in the interval (0, t) and (t, t+h) are independent) or ,
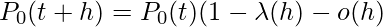 or
or 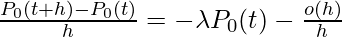 .
.
Taking limit as h tends to zero we get,
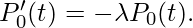 .
.
The solution of above differential equation is,
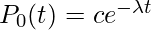 ,
,
taking the initial condition 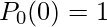 we evaluate c=0. Hence,
we evaluate c=0. Hence,
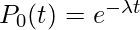 , so our claim is true for n=0.
, so our claim is true for n=0.
Now we try to prove it for n=1.
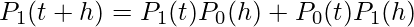
(We use the fact that the occurrence must be in either of the interval (0, t) and (t, t+h)), or
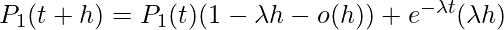 ,
,
or
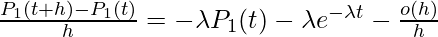 .
.
Again taking limit as h tends to zero,
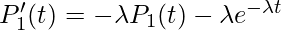 .
.
This is a first order linear differential equation and the solution is,
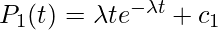
where 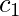 is a constant. Since,
is a constant. Since, 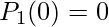 . We get,
. We get,
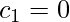 . Hence
. Hence 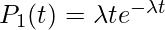 , or
, or 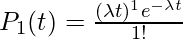 .
.
So our claim is true for n=1. We assume that our claim is true for n=m.
We will show that it is true for n=m+1. So,
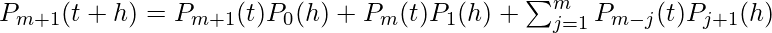 ,
,
(We assume that the m+1 occurrence can happen in different ways such as m+1 occurrences in (0, t) and no occurrence in (t, t+h) or m occurrences in (0, t) and 1. occurrence in (t, t+h), or m-j occurrences in (0, t) and j+1 occurrence in (t, t+h) for j=1 to m). So,
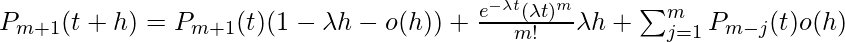
Since,
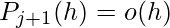 for j>=1.
for j>=1.
Or,
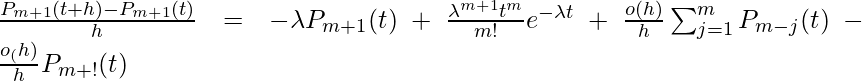
Taking limit as h goes to zero we have,
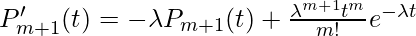 .
.
This is again a first order differential equation whose solution so,
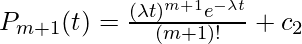 .
.
If e assume that 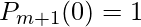 we get
we get 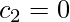 .
.
So the final result is,
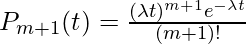 .
.
Hence the result is proved.
Thus we have derived the pmf of no. of occurrences in a Poisson Process which is a Poisson Distribution with parameter 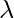 . Now if this
. Now if this 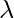 is a function of time we call the process as non-homogeneous Poisson process.
is a function of time we call the process as non-homogeneous Poisson process.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...