NCERT Solutions for Class 9 Maths Chapter 7 Triangles – This article contains detailed NCERT Solutions for Class 9 Maths Chapter 7 Triangles curated by the team of subject matter experts at GFG, to help students understand how to solve the NCERT problems easily.
Chapter 7 Triangles of NCERT for Class 9 Maths helps students understand the basic concepts of congruence of triangles and the rules of congruence. It is also helpful in understanding a few more properties of triangles and the inequalities in a triangle.
NCERT Chapter 7 Triangles in Class 9 covers topics such as :
This article provides solutions to all the problems asked in Class 9 Maths Chapter 7 Triangles of your NCERT textbook in a step-by-step manner as per the latest CBSE Syllabus 2023-24 and guidelines. Solutions to all the exercises in the NCERT Class 9 Maths Chapter 7 Triangles are regularly revised to check errors and updated according to the latest CBSE Syllabus 2023-24 and guidelines.
NCERT Solutions for Class 9 Maths Chapter 7 Triangles: Exercise 7.1
Question 1. In quadrilateral ACBD AC = AD and AB bisects ∠ A (see Fig. 7.16). Show that ∆ ABC ≅ ∆ ABD What can you say about BC and BD?

Solution:
Given that AC and AD are equal
i.e. AC = AD and the line AB bisects ∠A.
Considering the two triangles ΔABC and ΔABD,
Where,
AC = AD { As given}………………………………………… (i)
∠CAB = ∠DAB ( As AB bisects of ∠A)……………. (ii)
AB { Common side of both the triangle} …….. …(iii)
From above three equation both the triangle satisfies “SAS” congruency criterion
So, ΔABC ≅ ΔABD.
Also,
BC and BD will be of equal lengths as they are corresponding parts of congruent triangles(CPCT).
So BC = BD.
Question 2. ABCD is a quadrilateral in which AD = BC and ∠ DAB = ∠ CBA (see Fig. 7.17). Prove that
(i) ∆ ABD ≅ ∆ BAC
(ii) BD = AC
(iii) ∠ ABD = ∠ BAC.

Solution:
(i) Given that AD = BC,
And ∠ DAB = ∠ CBA.
Considering two triangles ΔABD and ΔBAC.
Where,
AD = BC { As given }………………………………………….. (i)
∠ DAB = ∠ CBA { As given also}……………………….. (ii)
AB {Common side of both the triangle)…………. (iii)
From above three equation two triangles ABD and BAC satisfies “SAS” congruency criterion
So, ΔABD ≅ ΔBAC
(ii) Also,
BD and AC will be equal as they are corresponding parts of congruent triangles(CPCT).
So BD = AC
(iii) Similarly,
∠ABD and ∠BAC will be equal as they are corresponding parts of congruent triangles(CPCT).
So,
∠ABD = ∠BAC.
Question 3. AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

Solution:
Given that AD and BC are two equal perpendiculars to a line segment AB
Considering two triangles ΔAOD and ΔBOC
Where,
∠ AOD = ∠ BOC {Vertically opposite angles}………………. (i)
∠ OAD = ∠ OBC {Given that they are perpendiculars}…. (ii)
AD = BC {As given}………………………………………………… (iii)
From above three equation both the triangle satisfies “AAS” congruency criterion
So, ΔAOD ≅ ΔBOC
AO and BO will be equal as they are corresponding parts of congruent triangles(CPCT).
So, AO = BO
Hence, CD bisects AB at O.
Question 4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ∆ ABC ≅ ∆ CDA.
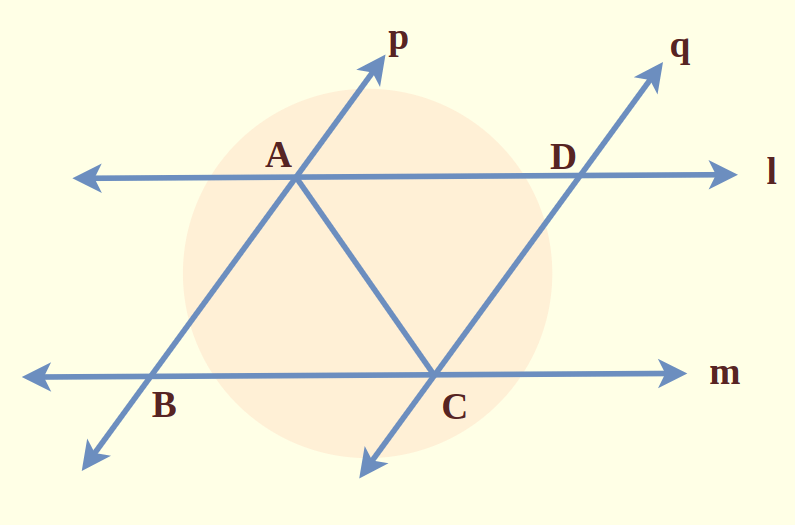
Solution:
Given that l and m are two parallel lines p and q are another pair of parallel lines
Considering two triangles ΔABC and ΔCDA
Where,
∠ BCA = ∠DAC {Alternate interior angles}…. (i)
∠ BAC = ∠ DCA {Alternate interior angles}…. (ii)
AC {Common side of two triangles}………….(iii)
From above three equation both the triangle satisfies “ASA” congruency criterion
So, ΔABC ≅ ΔCDA
Question 5. Line l is the bisector of an angle ∠ A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that:
(i) ∆ APB ≅ ∆ AQB
(ii) BP = BQ or B is equidistant from the arms of ∠ A.

Solution:
Given that, Line l is the bisector of an angle ∠ A and B
BP and BQ are perpendiculars from angle A.
Considering two triangles ΔAPB and ΔAQB
Where,
∠ APB = ∠ AQB { Two right angles as given }…… (i)
∠BAP = ∠BAQ (As line l bisects angle A }……… (ii)
AB { Common sides of both the triangle }……… (iii)
From above three equation both the triangle satisfies “AAS” congruency criterion
So, ΔAPB≅ ΔAQB.
(ii) Also we can say BP and BQ are equal as they are corresponding parts of congruent triangles(CPCT).
So, BP = BQ
Question 6. In Fig. 7.21, AC = AE, AB = AD and ∠ BAD = ∠ EAC. Show that BC = DE.

Solution:
Given that AC = AE, AB = AD
And ∠BAD = ∠EAC
As given that ∠BAD = ∠EAC
Adding ∠DAC on both the sides
We get,
∠BAD + ∠DAC = ∠EAC + ∠ DAC
∠BAC = ∠EAD
Considering two triangles ΔABC and ΔADE
Where,
AC = AE { As given }…………………… (i)
∠BAC = ∠EAD { Hence proven }…….. (ii)
AB = AD {As also given }……………….. (iii)
From above three equation both the triangle satisfies “SAS” congruency criterion
So, ΔABC ≅ ΔADE
(ii) Also we can say BC and DE are equal as they are corresponding parts of congruent triangles(CPCT).
So that BC = DE.
Question 7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB (see Fig. 7.22). Show that:
(i) ∆ DAP ≅ ∆ EBP
(ii) AD = BE

Solution:
Given that P is the mid-point of line AB, So AP = BP
Also, ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB
Now adding ∠DPE on both the sides of two equal angle ∠ EPA = ∠ DPB
∠ EPA + ∠ DPE = ∠ DPB + ∠DPE
Which implies that two angles ∠ DPA = ∠ EPB
Considering two triangles ∆ DAP and ∆ EBP
∠ DPA = ∠ EPB { Hence proven }…… (i)
AP = BP { Hence Given }……………… (ii)
∠ BAD = ∠ ABE { As given }…………..(iii)
From above three equation both the triangle satisfies “ASA” congruency criterion
So, ΔDAP ≅ ΔEBP
(ii) Also we can say AD and BE are equal as they are corresponding parts of congruent triangles(CPCT).
So that, AD = BE
Question 8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ∆ AMC ≅ ∆ BMD
(ii) ∠ DBC is a right angle.
(iii) ∆ DBC ≅ ∆ ACB
(iv) CM = 1/2 AB

Solution:
Given that M is the mid-point of AB
So AM = BM
∠ ACB = 90°
and DM = CM
(i) Considering two triangles ΔAMC and ΔBMD:
AM = BM { As given }………………………………………. (i)
∠ CMA = ∠ DMB { Vertically opposite angles }…. (ii)
CM = DM { As given also}……………………………….. (iii)
From above three equation both the triangle satisfies “SAS” congruency criterion
So, ΔAMC ≅ ΔBMD
(ii) From above congruency we can say
∠ ACD = ∠ BDC
Also alternate interior angles of two parallel lines AC and DB.
Since sum of two co-interiors angles results to 180°.
So, ∠ ACB + ∠ DBC = 180°
∠ DBC = 180° – ∠ ACB
∠ DBC = 90° { As ∠ACB =90° }
(iii) In ΔDBC and ΔACB,
BC { Common side of both the triangle }……. (i)
∠ ACB = ∠ DBC { As both are right angles }….(ii)
DB = AC (by CPCT)………………………………….. (iii)
From above three equation both the triangle satisfies “SAS” congruency criterion
So, ΔDBC ≅ ΔACB
(iv) As M is the mid point so we can say
DM = CM = AM = BM
Also we can say that AB = CD ( By CPCT )
As M is the mid point of CD we can write
CM + DM = AB
Hence, CM + CM = AB (As DM = CM )
Hence, CM = (½) AB
NCERT Solutions for Class 9 Maths Chapter 7 Triangles : Exercise 7.2
Question 1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC (ii) AO bisects ∠A
Solution:

Given: (i) An isosceles ∆ABC in which AB=AC
(ii) bisects of ∠B and ∠C each other at O.
Show: (i) OB=OC
(ii) AO bisects ∠A (∠1=∠2)
(i) In ∆ABC,
AB = AC
∠B =∠C [angles opposite to equal sides are equal]
1/2 ∠B = 1/2∠C
∠OBC=∠OCB
∴OB = OC [sides opposite equal ∠ are equal]
(ii) In ∆AOB and ADC
AB = AC [given side]
1/2 ∠B = 1/2∠C
∠ABO = ∠ACO [Angle]
BO = OC [proved above side]
∴∆AOB ≅ AOC
Thus ∠1 = ∠2
Therefore, AO bisects ∠A
Question 2. In ΔABC, AD is the perpendicular bisector of BC (see fig.). Show that ΔABC is an isosceles triangle in which AB = AC.

Solution:
Given: AD is ⊥ bisector of BC
Show: AB=BC
In ∆ABD and ∆ACD
BD=DC [AD is ⊥ bisector side]
∠ADB=∠ADC [Each 90° angle]
AD=AD [common side]
∴∆ABD≅∆ACD [S.A.S]
AB=AC [C.P.C.T]
Question 3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig.). Show that these altitudes are equal.

Solution:
Given: AB=AC,BE and CF are altitudes
Show: BE=CF
In ∆AEB and ∆AFC,
∠E=∠F [Each 90° angle]
∠A=∠A [common angle]
AB=AC [given side]
∴∆AEB≅∆AFC [A.A.S]
BE=CF [C.P.C.T]
Question 4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see fig. ). Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.

Solution:
Given: Altitudes BE and CF to sides AC and AB are equal
Show: (i) ΔABE ≅ ΔACF
(ii) AB = AC
(i) In ∆ABF and ∆ACF,
∠E=∠F [Each 90° angle]
∠A=∠A [common angle]
AB=AC [given] S
∴∆AEB≅∆AFC [A.A.S]
(ii) AB=AC [C.P.C.T]
Question 5. ABC and DBC are two isosceles triangles on the same base BC (see Fig.). Show that ∠ABD = ∠ACD.

Solution:
Given: AB=AC,BD=DC
Show: ∠ABD = ∠ACD
In ∆ABD,
AD=AC
∴∠1=∠2 [angle opposite to equal sides are equal] [1]
In ∆BDC,
BD=DC
∴∠3=∠4 [angle opposite to equal sides are equal] [2]
Adding 1 and 2
∠1+∠2= ∠2+∠4
∠ABD=∠ACD
Question 6. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig.). Show that ∠BCD is a right angle.

Solution:
In ∆ABC,
AB=AC
∠ACB=∠ABC [1]
In ∆ACD,
AC=AD
∠ACD=∠ADC [2]
Adding 1 and 2
∠ACB+∠ACD=∠ABC+∠ADC
∠BCD=∠ABC+∠BDC
Adding ∠BCD on both side
∠BCD+∠BCD=∠ABC+∠BDC+∠BCD
2∠BCD=180°
∠BCD=(180°)/2=90°
Question 7. ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Solution:

Find: ∠B=? and ∠C?
In ∆ABC,
AB=AC
∴∠B=∠C [angle opposite to equal side are equal]
∠A+∠B+∠C=180° [angle sum property of triangle]
90°+∠B+∠B=180°
2∠B=180°-90°
∠B=(90°)/2=45°
Therefore, ∠B=45° and ∠C =45°
Question 8. Show that the angles of an equilateral triangle are 60° each.
Solution:

Given: Let ∆ABC is an equilateral ∆
Show: ∠A=∠B=∠C=60°
In ∆ABC,
AB=AC
∠B=∠C [1]
Also
AC=BC
∠B=∠A [2]
From 1,2 and 2
∠A=∠B=∠C
In ∆ABC,
∠A+∠B+∠C=180° [angle sum property of triangle]
∠A+∠A+∠A=180°
3∠A=180°
∠A=(180°)/3=60°
∠A=60°
∴∠B=60° and ∠C=60°
NCERT Solutions for Class 9 Maths Chapter 7 Triangles: Exercise 7.3
Question 1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Figure). If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.
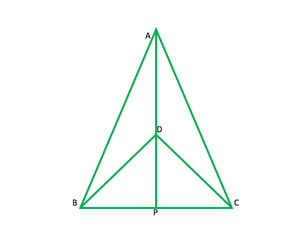
Solution:
Given: ∆ABC and ∆DCB are isosceles ∆on the same base BC.
To show:
- ΔABD ≅ ΔACD
- ΔABP ≅ ΔACP
- AP bisects ∠A as well as ∠D.
- AP is the perpendicular bisector of BC.
i) in ∆ABD and ∆ACB
AB=AC
BD=CD
AD=AD
∆ABD≅∆ACD ————-(S.S.S)
ii) in ∆ABP and ∆ACP
AB=AC
∠ BAP≅∠CAP [∆ABD≅∆ACD BY C.P.CT]
AP=AP ———[common]
∴[∆ABD≅∆ACD ———–[S.A.S]
iii) [∆ABD≅∆ACD ———–[S.A.S]
∠BAD=∠CAD
AD, bisects ∠A
AP, bisects ∠A —————–1
In ∆ BDP and ∆DPB
BD=CD —————(GIVEN)
DP=PC ———-[∆AB≅ ∆ACP C.P.C.T]
DP=DP ———–[common]
∴∆BDP≅∆CDP (S.S.S)
∠BDP=∠CDP (C.P.C.T)
DP bisects ∠D
AP bisects ∠D ——————-2
From 1 and 2, AP bisects ∠ A as well as ∠ D
iv) ∠ AP +∠APC =180° ————[linear pair]
∠APB=∠APC ————-[∆ABP≅∆ACP C.P.CT]
∠APB + ∠APC=180°
2 ∠ APB=180°
∠APB=180/2=90°
BP=PC (FROM ii)
∴AP is ⊥ bisects of BC.
Question 2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects ∠A.
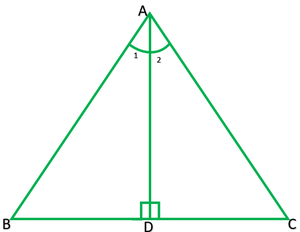
Solution:
Given: AB=AC, AD altitude
To Show:
(i) AD bisects BC (ii) AD bisects ∠A.
In ∆ADB and ∆ADC
∠ADB=∠ADC ——– ———–[each 90°] R
AB=AC ——————–[given]S
AD=AD ——–[common]S
∴ ∆ADB ≅∆ADC
BD=DC ————-[c.p.c.t]
∴AD bisects BC
∠1=∠2 ————-[c.p.c.t]
∴AD bisects ∠A
Question 3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ PQR
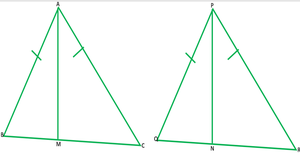
Solution:
Given:
AB=PQ
BC=QR
AM=PN
AM and PN are medians
To show:(i) ΔABM ≅ ΔPQN (ii) ΔABC ≅ PQR
Solution: In ΔABM and ΔPQN
AB=PQ
AM=PN
because AM and PN are medians BC=QR
therefore =1/2BC=1/2QR
∴BM=QN
∴) ΔABM ≅ ΔPQN ———[S.S.S]
∠B=∠Q ——–[c.p.c.t]
ii)now in ΔABC and ΔPQR
AB=PQ ———-[given]
∠B=∠Q from (i)
BC=QR —————-[given]
∴ ΔABC ≅ PQR [S.A.S]
Question 4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
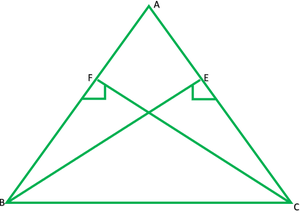
Solution:
Given: altitude BE and CF are equal
To prove: ΔABC is an isosceles Δ
In ΔBEC and ΔCEB
∠E=∠F —————-[each 90°] R
BC=BC —————–[common] H
BF=CF —————-[given] S
# ΔBEC ≅ ΔCEB [R.H.S]
∠C=∠B ————-[C.P.C.T]
In ΔABC,
∠C=∠B
Question 5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
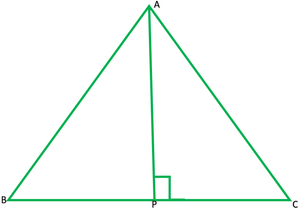
Solution:
Given:
In ∆ABC,
AB=BC
AP ⊥ BC
to show that: ∠B = ∠C.
Solution:
In ∆APB and ∆APC
∠APB = ∠APC —————[ each 90°] R
AB=AC ——————-[given] H
AP=AP ——————–[common] S
∴∆APB ≅ ∆APC ———-[R.H.S]
∠B = ∠C —————[C.P.C.T]
NCERT Solutions for Class 9 Maths Chapter 7 Triangles: Exercise 7.4
Question 1. Show that in a right-angled triangle, the hypotenuse is the longest side.
Solution:
Given: Right angle triangle intersect ∠B=90°
To show: AC>AB and AC>BC
Solution:∠A+∠B+∠C=180° —————-[angle sum property]
∠A+90°+∠C=180°
∠A+∠C=180°=90°
∠A+∠C=90°
∴∠A<90° and ∠C<90°
BC<AC AB<AC ———-[sides opposite to longer angle is greater]
∴Hypotenuse is the longest side.

Question 2. In Fig. 7.48, sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
Solution:

Given : ∠PBC < ∠QCB LET this be [∠1 < ∠2]
To Show : AD < BC
Solution: ∠1 < ∠2 ——–[given]
-∠1 > -∠2
180-∠1>180-∠2
∠3>∠4 ———[linear pair]
In ∆ABC,
∠3>∠4
AC>AB
Question 3. In Fig. 7.49, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.
Solution:

Given: ∠B < ∠A and ∠C < ∠D
To show: AD<BC
Solution: In ∆BOA
∠B < ∠A
∴AO<BO————-1
In ∆COD
∠C < ∠D
∴OD<OC————-2
Adding 1 and 2
AO+OD+<BO+OC
AD<BC
Question 4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50). Show that ∠A > ∠C and ∠B > ∠D.
Solution:

Given: AB is smaller side
CD is longest side
To show: ∠A > ∠C and ∠B > ∠D.
Solution : In ∆ABC
BC>AB
∠1>∠2 ———-[angle opposite to greater side is greatest]-1
In ∆ABC
CD>AD
∠3>∠4 ———[ angle opposite to greater side is greatest]-2
Adding 1 and 2
∠1+∠2+∠3+∠4
∠A>∠C
ii) In ∆ABD
AD>AB
∠5>∠6 ——————-[ angle opposite to greater side is greatest]-3
In ∆BCD
CD>BC
∠7>∠8 ——————-[ angle opposite to greater side is greatest]-4
Adding 3 and 4
∠5+∠6+∠7+∠8
∠B > ∠D
Question 5. In Fig 7.51, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.
Solution:

Given: PR>PQ
PS is angle bisects ∠QPR
To show: ∠PSR > ∠PSQ
Solution: PR>PQ
∴∠3+∠4 ————[angle opposite to greater side is larger]
∠3+∠1+x=180° ————-[angle sum property of ∆]
∠3=180°-∠1-x ————1
In ∆PSR
4+∠2+x=180° ————-[angle sum property of ∆]
∠4=180°-∠2-x ————2
Because ∠3>∠4
180°-∠1-x >180°-∠2-x
-∠1>-∠2
∠1<∠2
∠PSQ<∠PSR OR ∠PSR>∠PSQ
Question 6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest
Solution:

Given: Let P be any point not lying on a line L.
PM ⊥ L
Now, ∠ is any point another than M lying on line=L
In ∆PMN
∠M90° ———-[ PM ⊥ L]
∠L<90° ——-[∴∠M90° ∠L<90° ∠L<90°]
∠L<∠M
AM<PL ———[side opposite to greater is greater ]
NCERT Solutions for Class 9 Maths Chapter 7 Triangles : Exercise 7.5 (Optional)
Question 1. ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
Solution:

To obtain a point which is equidistant from all vertices of a triangle we construct perpendicular bisectors of all sides (AB, BC, CA) of the triangle (ΔABC). The point of intersection of these bisectors is known as Circumcenter(O) which is equidistant from all vertices.
Question 2. In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Solution:

To obtain a point which is equidistant from all sides of a triangle we construct angle bisectors of all angles present in ΔABC i.e ∠BAC, ∠ABC, ∠ACB. The point of intersection of these bisectors is called Incentre(I) which is equidistant from all sides.
Question 3. In a huge park, people are concentrated at three points :
A: where there are different slides and swings for children,
B: near which a man-made lake is situated,
C: which is near to a large parking and exit.
Where should an ice cream parlour be set up so that the maximum number of persons can approach it?
(Hint : The parlour should be equidistant from A, B and C)

Solution:

The ice-cream parlour must be set somewhere so that it’s easily available for the public. So for such point it should be at a equal distance from point A, B, C & such point is termed as circumcenter.
Question 4. Complete the hexagonal and star-shaped Rangolies by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?

Solution:

We need to find the number of triangles that can get fit the above figures i.e the hexagon and the star.
So,
Area of hexagon = (Area of small triangle inside hexagon) * 6
Area of small equilateral triangle = √3/4 * a2
= √3/4 * 52
= √3/4 * 25 = 25√3/4
So,
Area of hexagon = 25√3/4 * 6
= 150√3/4 cm2
Area of Star = Area of 6 triangles and 1 hexagon
= 6 * 25√3/4 + 150√3/4
= 300√3/4 cm2
Area of triangles of 1cm side that are to be fitted = √3/4 * 12
= √3/4 cm2
Number of triangles that can be accommodated inside hexagon and stars :
a. For Hexagon : Area of hexagon/ Area of 1cm side triangle
= 150√3/4 cm2 / √3/4 cm2
= 150 triangles
b. For Star : Area of star/ Area of 1cm triangle
= 300√3/4 cm2 / √3/4 cm2
= 300 triangles
Hence, the star can accommodate 150 more triangles than the hexagon.
Key Features of NCERT Solutions for Class 9 Maths Chapter 7 Triangles:
- These NCERT solutions are developed by the GfG team, with a focus on students’ benefit .
- NCERT Solutions are developed for each chapter of class 9 including Triangles.
- NCERT Solutions provides accurate and complete solutions for problems given in NCERT textbooks.
FAQs on NCERT Solutions for Class 9 Maths Chapter 7-Triangles
1. Why is it important to learn about Triangles?
One of the fundamental geometric forms is the triangle. Understanding polygonal characteristics and connections is based on them. Students build a solid geometric foundation by studying triangles, and they also gain understanding into the concepts of congruence, resemblance, and symmetry.
2. What topics are covered in NCERT Solutions for Class 9 Maths Chapter 7 Triangles?
NCERT Solutions for Class 9 Maths Chapter 7-Triangles covers topics such as congruence of triangles, their rules, attributes, and triangle inequalities.
3. How can NCERT Solutions for Class 9 Maths Chapter 7 Triangleshelp me?
NCERT Solutions for Class 9 Maths Chapter 7-Triangles can help you solve the NCERT exercise without any limitations. If you are stuck on a problem, you can find its solution in these solutions and free yourself from the frustration of being stuck on some question.
4. How many exercises are there in NCERT Solutions for Class 9 Maths Chapter 7 Triangles?
There are 3 exercises in the Class 9 Maths Chapter 7-Triangles which covers all the important topics and sub-topics.
5. Where can I find NCERT Solutions for Class 9 Maths Chapter 7 Triangles?
You can find these NCERT Solutions in this article created by our team of experts at GeeksforGeeks.
Share your thoughts in the comments
Please Login to comment...