CBSE Class 10 Maths Notes Chapter 3 Pair of Linear Equations in Two Variables provided by GeeksforGeeks, supports students’ education. We believe that students’ learning and development are of utmost importance, and that’s why we have created these comprehensive notes to help them comprehend the complex subject of Pair of Linear Equations in Two Variables better.
The NCERT Class 10 Maths textbook’s Chapter 3 explores the realm of Pair of Linear Equations in Two Variables and covers various concepts such as finding the solution of pair of Linear Equations in Two Variables using two methods and Conditions for solvability and more. Our notes aim to provide students with a complete summary of the entire chapter, including all essential topics, formulae, and concepts necessary to succeed in their exams.
What is Linear Equation in Two Variables?
Linear equations in two variables are characterized by having both variables raised to the highest exponent order of 1 and may have one, none, or infinitely many solutions. These equations are typically written in the standard form ax + by + c = 0, where x and y are the variables, and solutions are represented as ordered pairs such as (x, y). When graphed, a system of linear equations in two variables is represented by two straight lines, which may intersect, be parallel, or coincide.
Some examples of linear equations in two variable
- 3x − 2y + 1 = 0
- x + y − 2 = 0
Pair of Linear Equations in Two Variables
The general form of a pair of linear equations in two variables x and y is
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
Where,
a1, b1, c1, a2, b2, c2 are all real numbers 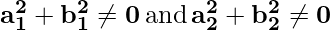
Solution of Simultaneous Linear Equation in Two Variables
The system of linear equations in two variables can be solved by the two method
- Algebraic Method
- Graphical Method
Algebraic Method
The most commonly used algebraic methods of solving a system of linear equations in two variables are:
- Substitution Method
- Elimination Method
- Cross Multiplication Method
Now, we will learn about these methods in detail.
Substitution Method
We can solve the given pair of linear equations using the Substitution Method by following the Steps discussed below,
Step 1: Solve for one variable in one of the equations.
Step 2: Substitute the expression obtained in Step 1 into the other equation, resulting in an equation that contains only one variable.
Step 3: Solve the equation from Step 2 for the variable.
Step 4: Substitute the solution from Step 3 into either of the original equations to find the value of the other variable.
Let’s learn about this method using the examples discussed below.
Example: Solve the following systems of equations by using the method of substitution 3x − 5y = −1 and x − y = −1.
Solution:
Solve x − y = −1 for x.
x = −1 + y
Substitute −1 + y for x in 3x − 5y = −1.
3 (−1 + y) − 5y = −1
⇒ −3 + 3y − 5y = −1
⇒ −2y = −1 + 3
⇒ −2y = 2
⇒ y = −1
Substitute −1 for y in 3x − 5y = −1.
3x − 5 ( −1)= −1
⇒ 3x + 5 = −1
⇒ 3x = −1 −5
⇒ 3x = −6
⇒ x = −2
Therefore, the solution of the given system of equation in two variable is x = −2 and y = −1.
Elimination Method
We can solve the given pair of linear equations using the Elimination method by following the Steps discussed below,
Step 1: To solve a system of linear equations, begin by writing both equations in standard form, and clearing any fractional coefficients.
Step 2: Select one variable to eliminate and make its coefficients opposite in the two equations.
Step 3: Multiply one or both equations so that the coefficients of the chosen variable become opposite.
Step 4: Add the resulting equations to eliminate that variable.
Step 5: Solve for the remaining variable, and substitute the solution into one of the original equations.
Step 6: Finally, solve for the other variable and express the solution as an ordered pair.
Let’s learn about this method using the examples discussed below.
Example 1: Solve the system of equations by using the elimination method x + y = 10 and x − y = 12.
Solution:
Both equations are in standard form.
Here, coefficient of y are opposite.
So, add the two equations to eliminate y and then solve for x.
(x + y) + (x − y) = 10 + 12
⇒ x + y + x − y = 22
⇒ 2x = 22
⇒ x = 11
Substitute 11 for x in x + y = 10 and the solve for y.
11 + y = 10
⇒ y = 10 − 11
⇒ y = −1
Therefore, the solution of the given system of equation in two variable is x = 11 and y = −1.
Example 2: Solve the system of equations by using the elimination method 3x + 2y = 11 and 2x + 3y = 4.
Solution:
Both equations are in standard form.
None of the coefficients are opposites.
Make the coefficients of y opposite by multiplying the first equation by −3.
−3 (3x + 2y) = −3 (11)
⇒ −9x − 6y = −33
Make the coefficients of y opposite by multiplying the second equation by 2.
2 (2x + 3y) = 2 (4)
⇒ 4x + 6y = 8
So, add the two equations −9x − 6y = −33 and 4x + 6y = 8 to eliminate y and then solve for x.
−9x − 6y + (4x + 6y) = −33 + 8
⇒ −9x + 4x = −25
⇒ −5x = −25
⇒ x = 5
Substitute 5 for x in 3x + 2y = 11 and the solve for y.
3 (5) + 2y = 11
⇒ 15 + 2y = 11
⇒ 2y = 11 − 15
⇒ 2y = −4
⇒ y = −2
Therefore, the solution of the given system of equation in two variable is x = 5 and y = −2.
Cross Multiplication Method
Let us consider the system of equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 such that a1 / a2 ≠ b1 / b2 then the system has a unique solution and that is given by:
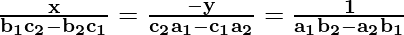
Example: Solve the system of equations using the method of cross multiplication x + y = 7 and 5x + 12y = 7
Solution:
Here, Here, a1 = 1 b1 = 1, c1 = -7, a2 = 5, b2 = 12, and c2 = -7
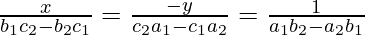
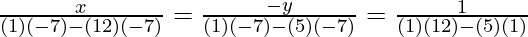
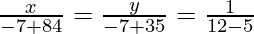
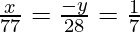
x = 11 and y = −4
Therefore, the solution of the given system of equation in two variable is x = 11 and y = -4.
Graphical Method
The graph of a pair of linear equations in two variables is represented by two lines.
- If the lines intersect at a point, then that point gives the unique solution of the two equations. In this case, the pair of equations is consistent.
- If the lines coincide, then there are infinitely many solutions — each point on the line being a solution. In this case, the pair of equations is dependent (consistent).
- If the lines are parallel, then the pair of equations has no solution. In this case, the pair of equations is inconsistent.
Example 1: Solve graphically the system of equations x + y = 3 and 3x − 2y = 4
Solution:
First, find the x-intercept and y-intercept.
For x-intercept, substitute 0 for y and then solve for x.
| First equation (x-intercept) | Second equation (x-intercept) |
|---|
|
x + 0 = 3
⇒ x = 3
|
3x − 2 (0) = 4
⇒ 3x = 4
⇒ y = 4/3
|
The x-intercept are (3, 0) and (4/3, 0).
For y-intercept, substitute 0 for x and then solve for y.
| First equation (y-intercept) | Second equation (y-intercept) |
|---|
|
0 + y = 3
⇒ y = 3
|
3 (0) − 2y = 4
⇒ −2y = 4
⇒ y = − 2
|
The y-intercept are (0, 3) and (0, −2).
Using these four point we can plot both the lines,
but we can find more point to plot, using the following method,
Solve x + y = 3 for y.
y = 3 − x
Solve 3x − 2y = 4 for y.
−2y = 4 − 3x
⇒ y = 3x/2 − 2
Make a xy table for y = 3 − x.
| x | y | (x, y) |
|---|
| 1 | 3 − 1 = 2 | (1, 2) |
| 2 | 3 − 2 = 1 | (2, 1) |
Make a xy table for y = 3x/2 − 2.
| x | y | (x, y) |
|---|
| 4 | 3(4)/2 − 2 = 4 | (4, 4) |
| 6 | 3(6)/2 − 2 = 7 | (6, 7) |
Plot the points on the graph and then drawing a line joining them.
Clearly, the two lines intersect at point (2, 1).
Therefore, the solution of the given system of equation in two variable is x = 2 and y = 1.
Example 2: Solve graphically the system of equations 2x + 4y = 10 and 3x + 6y = 12.
Solution:
First, find the x-intercept and y-intercept.
For x-intercept, substitute 0 for y and then solve for x.
| First equation (x-intercept) | Second equation (x-intercept) |
|---|
|
2x + 4 (0) = 10
⇒ 2x = 10
⇒ x = 5
|
3x + 6 (0) = 12
⇒ 3x = 12
⇒ x = 4
|
The x-intercept are (5, 0) and (4, 0).
For y-intercept, substitute 0 for x and then solve for y.
| First equation (y-intercept) | Second equation (y-intercept) |
|---|
|
2 (0) + 4y = 10
⇒ 4y = 10
⇒ y = 5/2
|
3 (0) + 6y = 12
⇒ 6y = 12
⇒ y = 2
|
The y-intercept are (0, 5/2) and (0, 2).
Using these four point we can plot both the lines,
but we can find more point to plot, using the following method,
Solve 2x + 4y = 10 for y.
4y = 10 − 2x
⇒ y = 5/2 − x/2
Solve 3x + 6y = 12 for y.
6y = 12 − 3x
⇒ y = 2 − x/2
Make a xy table for y = 5/2 − x/2.
| x | y | (x, y) |
|---|
| 3 | 5/2 − 3/2 = 1 | (3, 1) |
| 7 | 5/2 − 7/2 = −1 | (7, −1) |
Make a xy table for y = 2 − x/2.
| x | y | (x, y) |
|---|
| 2 | 2 − 2/2 = 1 | (2, 1) |
| 6 | 2 − 6/2 = −1 | (6, −1) |
Plot the points on the graph and then drawing a line joining them.
No two parallel lines have common points.
Hence, the given system of equations has no solution.
Example 3: Solve graphically the system of equations 3x − y = 2 and 9x − 3y = 6.
Solution:
Divide 9x − 3y = 6 by 3.
3x − y = 2
Now, both equations are same.
First, find the x-intercept and y-intercept.
For x-intercept, substitute 0 for y and then solve for x.
3x − 0 = 2
⇒ 3x = 2
⇒ x = 2/3
The x-intercept is (2/3, 0).
For x-intercept, substitute 0 for x and then solve for y.
3 (0) − y = 2
⇒ −y = 2
⇒ y = −2
The y-intercept is (0, −2).
Solve 3x − y = 2 for y.
− y = 2 − 3x
⇒ y = 3x − 2
Make a xy table for y = 3x − 2.
| x | y | (x, y) |
|---|
| 1 | 3 (1) − 2 = 1 | (1, 1) |
| 2 | 3 (2) − 2 = 4 | (2, 4) |
Plot the points on the graph and then drawing a line joining them.
The graph are coincident.
Hence, the given system of equations have infinitely many solutions.
Conditions for Solvability of Pair of Linear Equations
A pair of equations can have three conditions resulting in the solution of the equations. Let us consider the system of equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0.
Case 1: When a1b2 − a2b1 = 0 OR a1 / a2 ≠ b1 / b2
The given pair of equation are consistent and it has a unique solution.
Case 2: When a1b2 − a2b1 = 0 and a1c2 − a2c1 =0 OR a1 / a2 = b1 / b2 = c1 / c2
The system of equations has infinitely many solutions.
Case 3: When a1b2 − a2b1 = 0 and a1c2 − a2c1 ≠ 0 OR a1 / a2 = b1 / b2 ≠ c1 / c2
The given pair of equation are inconsistent and it has no solution.
Now let’s learn about all these cases in detail with the help of the example discussed below,
Example 1: Determine the system of equation 2x + 3y = 7 and 6x + 5y = 11 has a unique solution, no solution or infinitely many solutions.
Solution:
Here, a1 = 2, b1 = 3, c1 = −7, a2 = 6, b2 = 5, and c2 = −11.
a1 / a2 = 2 / 6
⇒ a1 / a2 = 1 / 3
b1 / b2 = 3 / 5
c1 / c2 = −7 / −11
⇒ c1 / c2 = 7 / 11
So, a1 / a2 ≠ b1 / b2 ≠ c1 / c2
Therefore, the system of equation has a unique solution and it is consistent.
Example 2: Determine the system of equation 6x + 5y = 11 and 9x + 15y/2 = 21 has a unique solution, no solution or infinitely many solutions.
Solution:
Here, a1 = 6, b1 = 5, c1 = −11, a2 = 9, b2 = 15/2, and c2 = −21
a1 / a2 = 6 / 9
⇒ a1 / a2 = 2/3
b1 / b2 = 5 / 15/2
⇒ b1 / b2 = 10 / 15
⇒ b1 / b2 = 2 / 3
c1 / c2 = −11 / −21
c1 / c2 = 11 / 21
So, a1 / a2 = b1 / b2 ≠ c1 / c2
Therefore, the system of equation has no solution and it is inconsistent.
Example 3: Determine the system of the equation −3x + 4y = 5 and 9x/2 − 6y + 15/2 = 0 has a unique solution, no solution or infinitely many solutions.
Solution:
Here, a1 = −3, b1 = 4, c1 = −5, a2 = 9 / 2, b2 = −6, and c2 = 15 / 2
a1 / a2 = −3 / 9/2
⇒ a1 / a2 = −6 / 9
⇒ a1 / a2 = − 2 / 3
b1 / b2 = 4 / −6
⇒ b1 / b2 = −2 / 3
c1 / c2 = −6/ 15/ 2
⇒ c1 / c2 = −12 / 15
⇒ c1 / c2 = −4 / 5
So, a1 / a2 = b1 / b2 ≠ c1 / c2
Therefore, the system of equation has infinitely many solutions.
Equation Reducible to a Pair of Linear Equations in Two Variables
The solutions of such pairs of linear equations in two variables are not linear at a glance but can be reduced to linear form by making some suitable substitution.
Example: Solve the system of linear equations 2/x + 2/3y = 1/6 and 3/x + 2/y = 0.
Solution:
Assume u = 1/x and v = 1/y
Rewrite the system of equation in terms of u and v.
2u + 2v/3 = 1/6 and 3u + 2v = 0
Solve 3u + 2v = 0 for u.
u = -2v/3
Substitute -2v/3 for u in 2u + 2v/3 = 1/6.
2(-2v/3) + 2v/3 = 1/6
⇒ -2v/3 = 1/6
⇒ v = -1/4
Substitute -1/4 for v in u = -2v/3.
u = -2/3 × -1/4
⇒ u = 1/6
Now, substitute the value of u and v in u = 1/x and v = 1/y
1/6 = 1/x
⇒ x = 6
-1/4 = 1/y
⇒ y = -4
Therefore, the solution of the given system of equation in two variable is x = 6 and y = -4.
FAQs on Pair of Linear Equations in Two Variables
Q1: What is a Pair of Linear Equations in Two Variables?
Answer:
A pair of linear equations in two variables is a pair of linear equations (i.e., the highest power of the variable is 1) and involve two variables. Mathematically we can write a pair of linear equations in two variables as:
Where a, b, c, d, e, and f are constants.
Q2: What is the Solution to a Pair of Linear Equations in Two Variables?
Answer:
The solution to a pair of linear equations in two variables is the set of values for the variables that satisfy both equations simultaneously. Geometrically, the solution represents the point (if it exists) where the lines corresponding to the equations intersect on a coordinate plane.
Q3: How can I solve a Pair of Linear Equations in Two Variables?
Answer:
We can solve a Pair of Linear Equations in Two Variables, using the following methods:
- Algebraic Methods
- Substitution Method
- Elimination Method
- Cross Multiplication Method
- Graphical Method
Q4: What is Graphical Method of Solving a Pair of Linear Equations in Two Variables?
Answer:
When equations are plotted on the graph and both the equation have some common part i.e., intersection. Then that intersection is called solution to the given pair of equations. This method of solving a Pair of Linear Equations in Two Variables is called the graphical method.
Q5: What does it Mean if a Pair of Linear Equations has no Solution?
Answer:
If a pair of linear equations has no solution, it means if we plot those lines on the graph, we will see parallel lines which never intersect. This case of Pair of Linear Equation is called inconsistent as there is no common solution of the equations.
Q6: Can a Pair of Linear Equations have infinitely many solutions?
Answer:
Yes, a pair of linear equations can have infinitely many solutions as two equations with the same graphs can overlap with each other and can have infinitely many possible solutions.
Share your thoughts in the comments
Please Login to comment...