NCERT Solutions for Class 9 Maths Chapter 10 Circles is a curated article by professionals at GFG, to help students solve problems related to circles with ease. All the solutions provided here are factually correct and
The NCERT Class 9 Maths Chapter 10 Circles covered a variety of issues, including how to determine the separation between equal chords from the centre and the angles that a chord at a location subtended. There are also studies of cyclic quadrilaterals and their properties, as well as the angles that a circle’s arc subtends.
NCERT solutions for Class 9 Maths Chapter 10 Circles: Exercise 10.1
Question 1: Fill in the blanks
(i) The centre of a circle lies in ____________ of the circle. (exterior/ interior)
Answer: Interior.
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in ______________ of the circle. (exterior/ interior)
Answer: Exterior.
(iii) The longest chord of a circle is a ______________ of the circle.
Answer: Diameter.
(iv) An arc is a _____________ when its ends are the ends of a diameter.
Answer: Semicircle.
(v) Segment of a circle is the region between an arc and _____________ of the circle.
Answer: Chord.
(vi) A circle divides the plane, on which it lies, in _______________ parts.
Answer: Three.
Problem 2: Write True or False: Give reasons for your answers.
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
Answer: True, Any line segment drawn from the centre of the circle to any point on it is called radius of the circle and will be of equal length.
(ii) A circle has only finite number of equal chords.
Answer: False, There can be infinite number of equal chords in a circle.
(iii) If a circle is divided into three equal arcs, each is a major arc.
Answer: False, When the arcs are not equal we will have major and minor arc, equal arcs cannot be classified as a major arc or a minor arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
Answer: True, Diameter is the longest chord of the circle and the length of the longest chord in a circle is twice the length of radius of the circle.
(v) Sector is the region between the chord and its corresponding arc.
Answer: False, Sector is defined as the region between the arc and 2 radii of the circle.
(vi) A circle is a plane figure
Answer: True, A circle is a 2D figure which can be drawn on a plane.
NCERT solutions for Class 9 Maths Chapter 10 Circles: Exercise 10.2
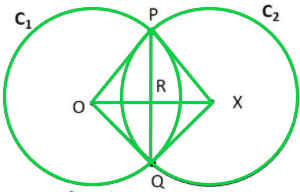
Question 1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Solution:
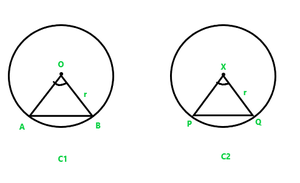
Given:
Two Congruent Circles C1 and C2
AB is the chord of C1
and PQ is the chord of C2
AB = PQ
To Prove: Angle subtended by the Chords AB and PQ are equal i.e. ∠AOB = ∠PXQ
Proof:
In △AOB & △PXQ
AO = PX (Radius of congruent circles are equal)
BO = QX (Radius of congruent circles are equal)
AB = PQ (Given)
△AOB ⩭ △PXQ (SSS congruence rule)
Therefore, ∠AOB = ∠PXQ (CPCT)
Question 2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Solution:

Given:
Two Congruent circles C1 and C2
AB is the chord of C1 and PQ is chord of C2
& ∠AOB = ∠PXQ
To prove :
In △AOB and △PXQ ,
AO = PX (Radius of congruent circles are equal)
∠AOB = ∠PXQ (Given)
BO = QX (Radius of congruent circles are equal)
△AOB ⩭ △PXQ (SAS congruence rule)
Therefore, AB = PQ (CPCT)
NCERT solutions for Class 9 Maths Chapter 10 Circles: Exercise 10.3
Question 1. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
(i) Two points common
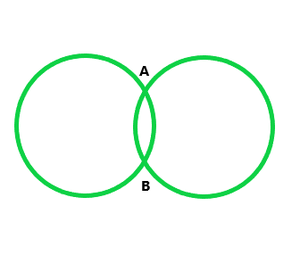
(ii) One point common
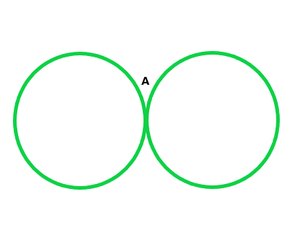
(iii) One point common

(iv) No point common

(v) No point common

As we can analyse from above, two circles can cut each other maximum at two points.
Question 2. Suppose you are given a circle. Give a construction to find its centre.
Solution:
Let the circle be C1
We need to find its centre.
Step 1: Take points P, Q, R on the circle
Step 2: Join PR and RQ.
We know that perpendicular bisector of a chord passes through centre
So, we construct perpendicular bisectors of PR and RQ
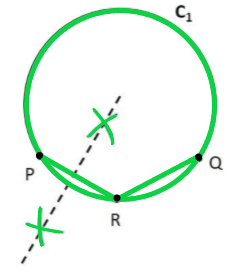
Step 3: Take a compass. With point P as pointy end and R as pencil end of the compass, mark an arc above and below PR. Do same with R as pointy end P as pencil end of the compass.
Step 4: Join points intersected by the arcs.
The line formed is the perpendicular bisector of PR.
Step 5: Take compass, with point R as pointy end and Q as pencil end of the compass mark an arc above and below RQ.
Do the same with Q as pointy end and R as pencil end of the compass
Step 6: Join the points intersected by the arcs.
The line formed is the perpendicular bisector of RQ.
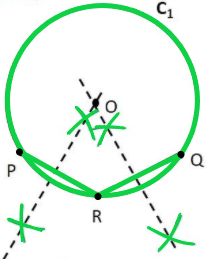
Step 7: The point where two perpendicular bisectors intersect is the centre of the circle. Mark it as point O.
Thus, O is the centre of the given circle.
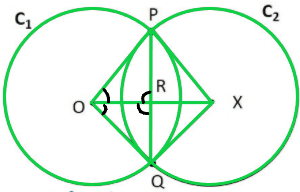
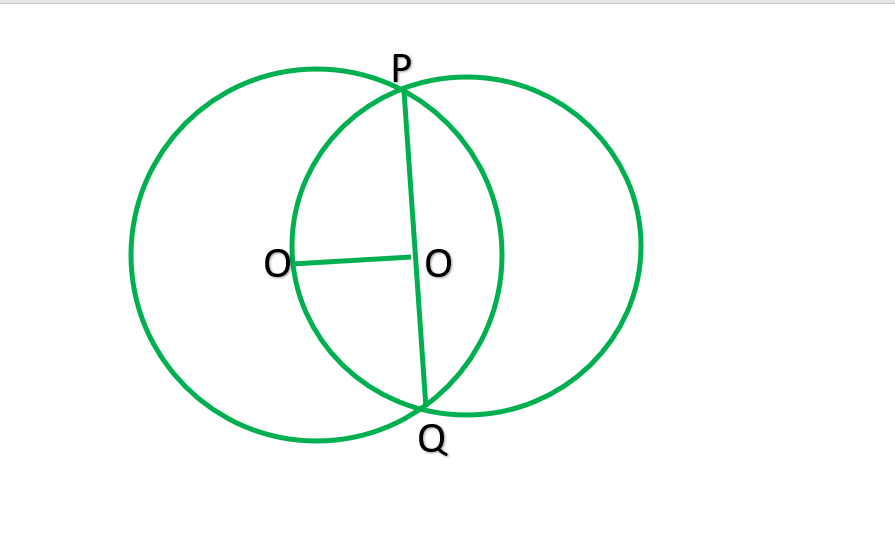
Question 3: If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
Given,
Let circle C1 have centre O and circle C2 have centre X, PQ is the common chord.
To prove: OX is the perpendicular bisector of PQ i.e.
1. PR = RQ
2. ∠PRO = ∠PRX = ∠QRO = ∠QRX = 90°
Construction:
Join PO, PX, QO, QX
Proof:
In △POX and △QOX
OP = OQ (Radius of circle C1)
XP = XQ (Radius of circle C2)
OX = OX (Common)
∴ △POX ≅ △QOX (SSS Congruence rule)
∠POX = ∠QOX (CPCT) —-(1)
Also,
In △POR and △QOR
OP = OQ (Radius of circle C1)
∠POR = ∠QOR ( From (1))
OR = OR (Common)
∴ △OPX ≅ △OQX (SAS Congruence Rule)
PR = QR (CPCT)
& ∠PRO = ∠QRO (CPCT) —-(2)
Since PQ is a line
∠PRO + ∠QRO = 180° (Linear Pair)
∠PRO + ∠PRO= 180° ( From (2))
2∠PRO = 180°
∠PRO = 180° / 2
∠PRO = 90°
Therefore,
∠QRO = ∠PRO = 90°
Also,
∠PRX = ∠QRO = 90° (Vertically opposite angles)
∠QRX = ∠PRO = 90° (Vertically opposite angles)
Since, ∠PRO = ∠PRX = ∠QRO = ∠QRX = 90°
∴ OX is the perpendicular bisector of PQ
NCERT solutions for Class 9 Maths Chapter 10 Circles: Exercise 10.4
Question 1. Two circles of radii 5cm and 3cm intersect at two points and the distance between their centers is 4 cm. Find the length of the common chord.
Solution:
Given: OP=4cm, AP=3cm, QR=5cm
To find: In ∆APO:
AO²=5²=25
OP²=4²=16
AP²=3²=9
OP²+AP²=AO²
BY converse of Pythagoras theorem
ΔAPO: is a right ∠D=P
Now, in the bigger circle OP is perpendicular AB
AP=½AB —————-(perpendicular from the center of circle to a chord bisect the chord )
3=½AB
6=AB
∴Therefore the length of common chord is 6cm.
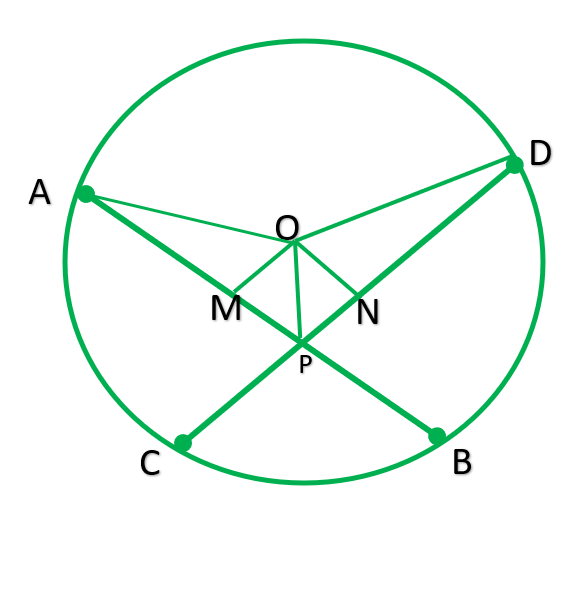
Question 2. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
Solution:
Given: Equal chord AB & CD intersect at P.
To find: AP=PD and PB=PC
Construction: Draw OM perpendicular AB ,ON perpendicular CD and join OP.
Because perpendicular from center bisect the chord
∴AM=MB=½AB also CN=ND=½CD
AM=MB=CN=ND ——————1
Now, In ∆OMP and ∆ONP
ANGLE M=ANGLE N [90° both]
OP=OP [COMMON]
ON=OM [equal chords are equilateral from center]
∴∆OMP≅∆ONP
Therefore MP=PN (C.P.C.T.) ——————2
i)from 1 and 2
AM+MP=ND+AN
AP=PD
ii)MB-MP=CN=PN
PB=PC
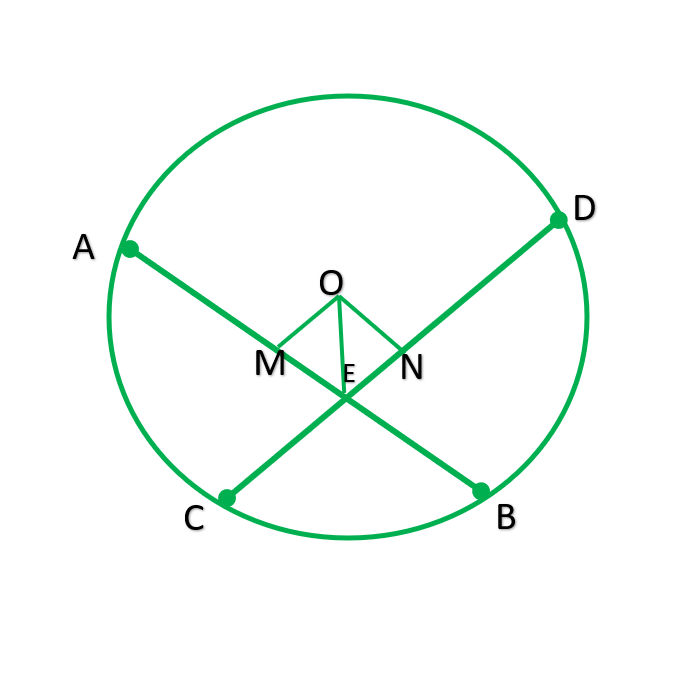
Question 3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the Centre makes equal angles with the chords.
Solution:
Given: Equal chords AB and CD intersect at P.
To prove: angle1=angle=2
Construction: Draw OM perpendicular AB & ON perpendicular CD.
Solution: In ∆OMP & ∆ONP
Angle M= Angel N [90 ° each]
OP=OP [common]
OM=ON —————[ Equal chords are equal distant from center]
∴∆OMP≅∆ONP ———-[R.H.S]
∴∠1=∠2 ———–[C.P.C.T]
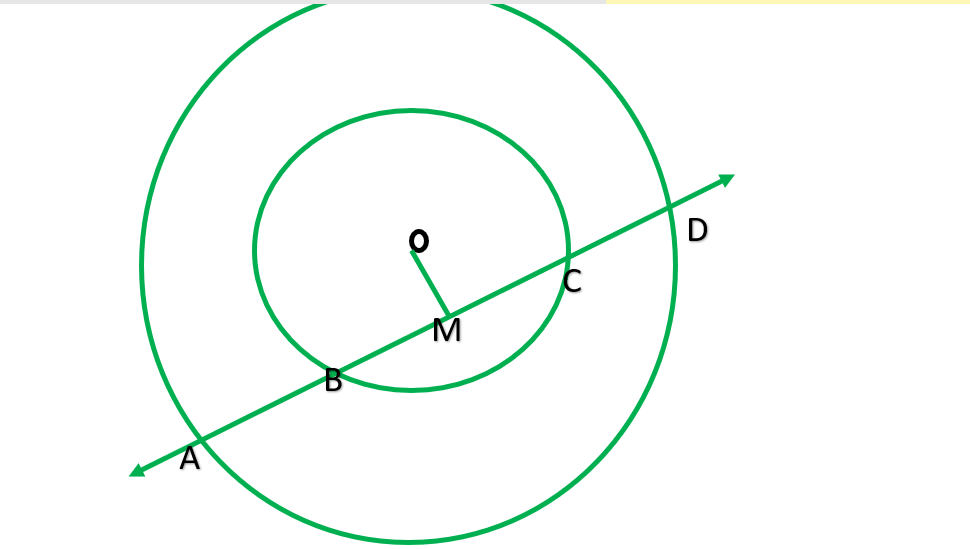
Question 4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see Figure).
Solution:
Given : two concentric circle with O. A line intersect them at A, B, C , and D
To prove: AB=CD
construction: Draw OM ⊥ AD ,In bigger circle AD is chord OM ⊥ AD.
∴AM=MD —————-[⊥ from center of circle of a circle bisects the chord] __________ 1
The smaller circle :
BC is chord OM ⊥ BC
BM=MC ——————-[⊥ from center of circle of a circle bisects the chord] __________ 2
subtracting 1-2
AM-BM=MD-MC
AB=CD
Question 5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
Solution:
To find RM=?
Let Reshma, Salma and Mandip be R,S,M
Construction: Draw OP ⊥ RS join OR and OS.
RP=½RS ___________[⊥ from center bisects the chord]
RP=½*6=3m
In right ΔORP
OP²=OR²- PR²
OP= √ 5² -3²
=√259 =√16 =4
Area of ΔORS=½*RS*OP
=½*6*4=12m² —————–1
Now, ∠N=90°
Area of ΔORS=½*SO*RN
=½*SO*RN ——————-2
Above ,1=2
12=½*5*RN
12/5*2=RN
RN=4.8
RM=2*RN _________________[⊥ from center bisects the chord]
=2*4.8
9.6m
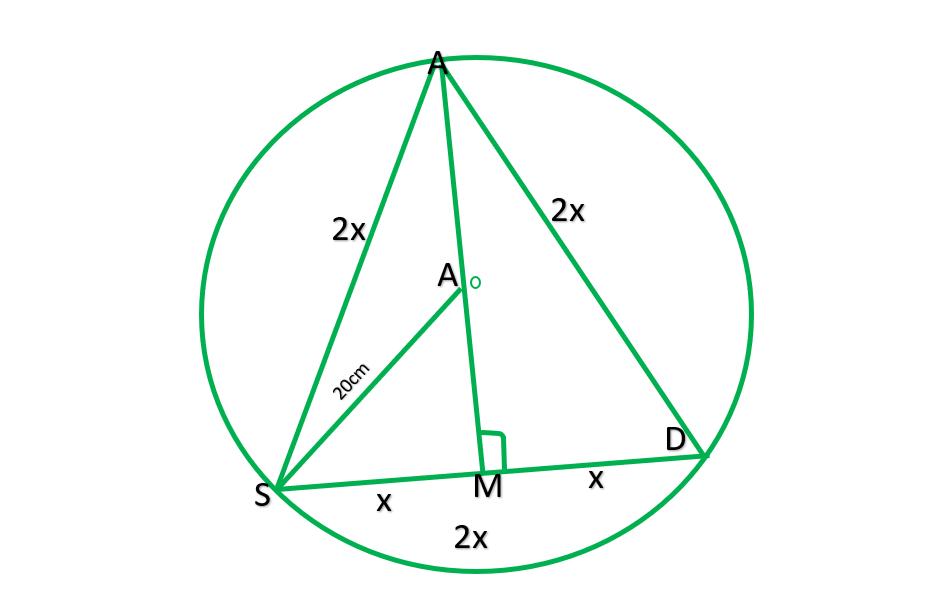
Question 6. A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary. Each boy has toy telephone in his hand to talk with each other. Find the length of the string of each phone.
Solution:
Draw AM⊥SD
AS=SD=AD
∴ASD is the equilateral Δ
Let each side of Δ-2xm
SM=2x/2=x
Now in Δ DMS, by the Pythagoras theorem
AM²+SM²=AS²
AM²= AS²- SM²
AM=√(2x²+x² )
==√(3x² )
AM =√3x
OM=AM-AO
OM=√3x-20
Now in right ΔOMS
OM²+SM²=SO²
(√3x-20)²+2x²+x²=20²
20²+400-40√3x+x^2=400
4x²=40√3x
4xx=40√3x
X=(40√3)/4
X=10√3x
Length of each string =2x
=2*10√3xm
NCERT solutions for Class 9 Maths Chapter 10 Circles: Exercise 10.5
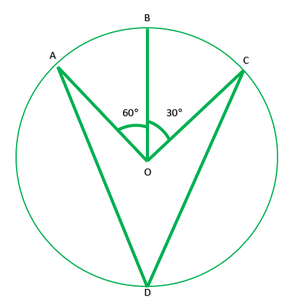
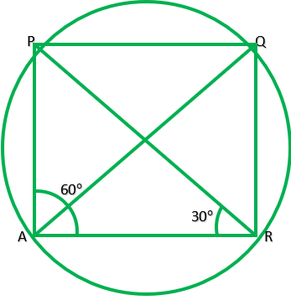
Question 1.In fig. 10.36, A, B, and C are three points on a circle with Centre O such that ∠BOC=30° and ∠AOB=60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
Solution:
Given: ∠BOC=30° and ∠AOB=60°
To find: ∠ADC
Solution: ∠AOC=2∠ADC ———[The angle subtended by an arc at the centre is double the angle the angle subtended by it any point on the remaining part of the circle.]
∠AOB+∠BOC=2∠ADC
60°+30°=2∠ADC
90+30=2∠ADC
90/2=∠ADC
45=∠ADC
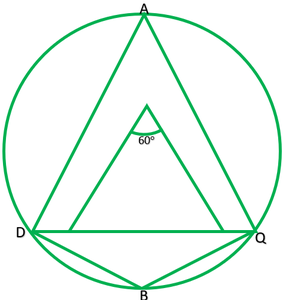
Question 2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
Given: PQ=OP
To find: Angle on major arc is ∠A=?
Angle on the minor arc is ∠B=?
Since, =PO=OQ
∴∠POQ=60°
∠POQ=2∠PAQ [The angle subtended by an arc at the centre is double the angle subtended by it any point on the remaining point of the circle]
Reflex ∠POQ=360°-60°
Reflex ∠POQ=300°
Reflex ∠POQ=2∠POQ
300°=2∠PBQ
300°/2=∠PBQ
150°=∠PBQ
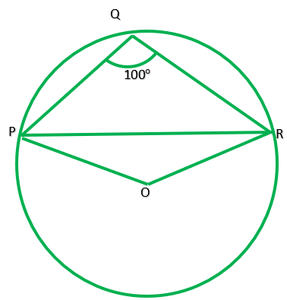
Question 3. In fig. 10.37, ∠PQR=100°,where P, Q and R are the points on a circle with centre O. Find ∠OPR.
Solution:
Given: ∠PQR=100°
To find: ∠OPR=?
Reflex ∠POR=2∠PQR ——–[ The angle subtended by an arc at the centre is double the angle subtended by it any point on the remaining point of the circle]
Reflex ∠PQR=2*100
=200°
∠POR=360°-200°
Now in ∆POR,OP=QR [ Radii of same circle]
∠P=∠R and let each =x.
∴∠P+∠O+∠R=180° [angle sum property of ∆]
x+160°+x=180°-160°
2x+160°=180°
x=20°/2=10°
∴∠OPR=10°
Question 4. In fig. 10.38, ∠ADC=69°,∠ACB=31°,find ∠BDC.
Solution:
Given: ∠ABC=69°,∠ACB=31°
To find: ∠BDC=?
Solution: In ∆ABC
∠A+∠B+∠C=180° ———[Angle sum property of ∆]
∠A+69°+31°=180°
∠A=180°-100°
∠A=80°
∠A and ∠D lie on the same segment therefore,
∠D=∠A
∠D=80°
∠BDC=80°
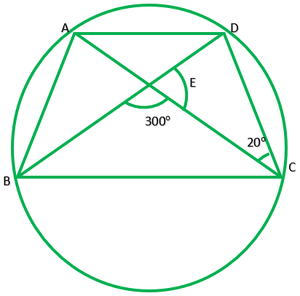
Question 5. In fig., A, B, C and D are four points on a circle.AC and BD intersect at a point E such that ∠BEC=130° and ∠ECD=20°. Find ∠BAC.
Solution:
Given: ∠BEC=130°,∠ECD=20°
To find: ∠BAC?
Solution: In ∆EDC
∠E=180°-130° ———[linear pair]
∠E=50°
∠E+∠C+∠D=180° ——[angle sum property of triangle]
50°+20°+∠D=180°
70°+∠D=180°
∠D=180/70=110°
Since, ∠A and ∠D line in the same segment
∴∠A=∠D
∠A=110°
∠BAC=110°
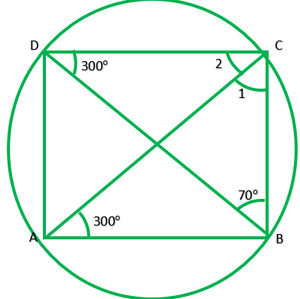
Question 6. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC =70°, ∠BAC is 30°, find ∠BCD. Further, if AB=BC, find ∠ECD.
Solution:
Given: ABCD is a cyclic quadrilateral diagonal intersect at E ∠DBC=70°, ∠BAC is 30°. If AB=BC.
To find: ∠BCD and ∠ECD
∠BDC=∠BAC=30° ——-[angle in the same segment]
In ∆BCD,
∠B+∠C+∠D=180° ——–[angle sum property of triangle]
∠C+100°=180°
∠C=180°-100°=80°
∴∠BCD=80°
If AB=BC,
Then, ∠BAC=∠BCA
30°=∠BCA
Now, ∠BCA+∠ECD=∠BCD
30°+∠ECD=80°
∠ECD=80°-30°
∴∠ECD=50°
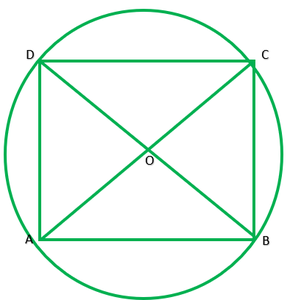
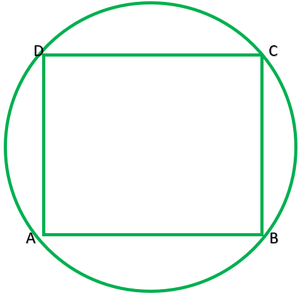
Question 7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Solution:
Given: ABCD is a cyclic quadrilateral. Diagonals of ABCD are also diameters of circle.
To prove: ABCD is a rectangle
AC=BD ———-[diameters of same circle]
OA=OA ———[radii of the same circle]
OA=OC=1/2AC ———2
OB=OD=1/2BD ———-2
From I and 2 diagonals are equal and bisect each other
∴ABCD is a rectangle
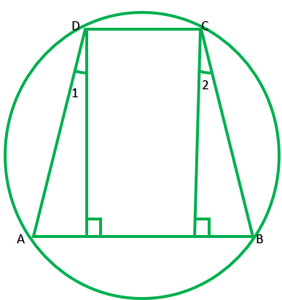
Question 8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Solution:
Draw DL perpendicular AB and EF perpendicular AB
In ∆DEA and ∆CEB
∠E=∠F ——–[each 90°]
AD=BC ——–[given]
DE=CF ——–[distance between || lines is same every line]
∴∆DEA≅∆CFB ——–[R.H.S]
∠A=∠B ———[by c.p.c.t.] 1
∠1=∠2 (from 1)
Adding 90° on each sides
∠1+90°=∠2+90°
∠1+∠EDC=∠2+FCD
∠ADC=∠BCD
∠D=∠C 2
Now,
∠A+∠A+∠C+∠C=360°
2∠A+2∠C=360°
2(∠A+∠C)=360°
∠A+∠C=360°/2=190°
Because sum of opposite angles is 180°.
ABCD is parallelogram.
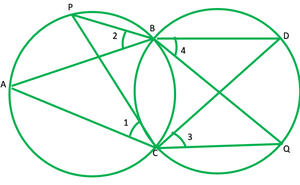
Question 9. Two circles intersect at two points B and C. Through B, two-line segments ABD and PBQ are drawn to intersect the circles at A, D, and P, Q respectively (see fig. 10.40). Prove that ∠ACP=∠QCD.
Solution:
To prove: ∠ACP=∠QCD or ∠1=∠2
∠1=∠2 —— [angles in the same segment are equal] 1
∠ 3=∠ 4 ——- [angles in the same segment are equal] 2
∠2=∠4 ——- [vertically opposite angles] 3
From 1 2 and 3
∠1=∠3
∴∠ACP=∠QCB
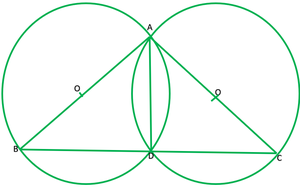
Question 10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Solution:
Given: ABC is ∆ and AB and AC are diameters of two circles
To prove: Point of intersection is D, lies on the BC.
Construction: Join AD
∠ADB=90° ——-[angles in semicircle] 1
∠ADC=90 ° ——[angles in semicircle] 2
Adding 1 and 2
∠ADB+∠ADC=90°+90°
∠BDC=180°
BDC is a straight line therefore D lies on BC.
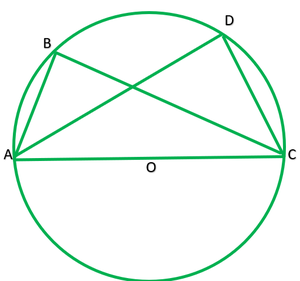
Question 11. ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
Solution:
Given: ABC and ADC are two right angle triangles with common hypotenuse AC.
To prove: ∠ADB=∠CBD
Solution: ∠ABC=∠ADC=90°
Circle drawn by taking AC as diameter passes through B and D.
For chord CD
∠CAD=∠CBD ——-[angle in the same segment]
Question 12. Prove that a cyclic parallelogram is rectangle.
Solution:
Given: ABC is a cyclic ||gm
To prove: ABCD is a rectangle.
Because ABCD is a cyclic ||gm
∴∠A+∠C=180°
∠A=∠C [opposite angle of ||gm]
∴∠A=∠C=(180°)/2=90°
∠A=90°
∠C=90°
Similarly,
∠B+∠D=180°
∴∠B=∠D =(180°)/2=90° ———-[opposite of a ||gm]
Each angle of ABCD is 90°
∠B=90°
∠D=90°
Thus, ABCD is a rectangle.
NCERT solutions for Class 9 Maths Chapter 10 Circles: Exercise 10.6
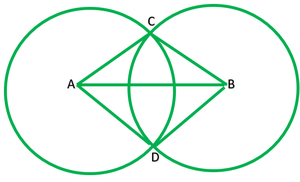
Question 1. Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution:
Given: Two circles with Centre A and B circle intersects at C and D.
To prove: ∠ACB=∠ADB
Construction: Join AD,BC and BD
Proof: In ∆ACB and ∆ADB
AC=AD ——–[radii of the same circle]
BC=BD ———[radii of the same circle]
AB=AB ——–[common]
∴∆ACB≅∆ADB ——— [by S.S.S]
∠ACB=∠ADB ——–[c.p.c.t.]
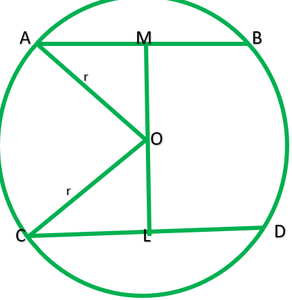
Question 2. Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution:
Let O be the centre of circle and be r cm
Given: AB=5cm, CD =11cm
Construction: Draw OM perpendicular AB and OL perpendicular CD.
Because OM perpendicular AB and OL perpendicular CD and AB||CD.
∴Points O,L, and M are collinear, than ∠M=6cm
Let OL=x
Then OM=6=x
Join AO and CO
OA=OC =r
OL=1/2CD=1/2*11=5.5cm —–[perpendicular from bisects the chord]
AM=1/2AB=1/2*5=2.3cm —–[perpendicular from bisects the chord]
Now, In right ∆DLC
r2=(OL)2+(CL)2
r2=x2+(5.5)2
r2=x2+30.25 ———–1
Now in right ∆OMA
r2=(OM)2+(MA)2
r2=(6-x)2+(2.5)2
r2=36+x2=12x+6.25
r2=x2-12x+42.25 ———–2
Now equating equation 1 and 2
X2+30.25=x2-12x+30.25
12x=42.25-30.25
X=12/12=1
Putting value of x in equation 1
r2=x2+30.25
r2=(1)2+30.25
r2=31.25
r=√31.25=5.6 (approx.)
Radius of circle is 5.6cm.
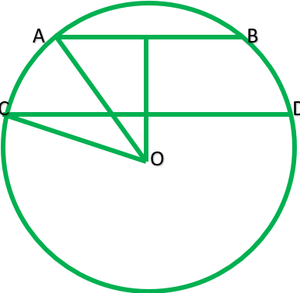
Question 3. The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the center, what is the distance of the other chord from the centre?
Solution:
Let AB and CD are|| chord of circle with centre O which AB=6cm and CD=8cm and radius of circle =r cm.
Construction: Draw OP perpendicular AB and OM perpendicular CD.
Because AB||CD and OP perpendicular AB and OM perpendicular CD therefore. Point O, M and P are collinear.
Clearly, OP=4cm ———-[According to question]
OM=to find?
P is midpoint of AB.
∴AP=1/2 AB=1/2*6=3cm
M is midpoint of AB.
CM=1/2 CD=1/2*8cm=4cm
Join AO and CO
Now in Right ∆OPA,
r2=AP2+PO2
r2=32+42
r2=9+16=25
Now in ∆OMC
r2=CM2+MO2
25=42+MO2
25-16=MO2
9=MO2
√9=MO
3=MO
∴Therefore distance of the other chord from the centre is 3cm
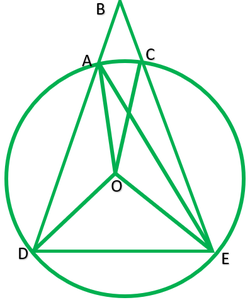
Question 4. Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution:
Give: Vertex B of ∆ABC lie outside the circle,chord AD=CE
To prove: ∠ABC=1/2(∠DOE-∠AOC)
Construction: Join AE
Solution: Chord DE subtends ∠DOE at the center and ∠DAE at point A on the circle.
∴∠DAE=1/2∠DOE ———-1
chords AC subtends ∠AOC at the centre and ∠AEC at point
∴∠AEC=1/2∠AOC ———2
In ∆ ABE,∠DAE is exterior angle
∠DAE=∠ABC +∠AEC
1/2∠DOE=∠ABC+1/2∠AOC
½(∠DOE-∠AOC)= ∠ABC
Question 5. Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Solution:
Given: A rhombus ABCD in which O is intersecting point of diagonals AC and BD.
A circle is drawn taking CD as diameter.
To prove: circle points through O or Lies on the circles.
Proof: In rhombus ABCD,
∠DOA=90° ——–[diagonals of rhombus intersect at 90°] 1
In circle:
∠COD=90° ——–[angle made in segment O is right angle] 2
From 1 and 2
O lies on the circle.
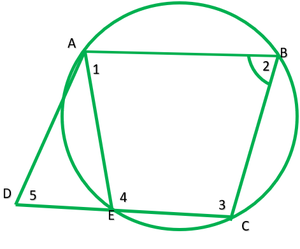
Question 6. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Solution:
ABCD is a ||gm. The circle through A,B and C intersect at E.
To prove: AE=AD
Proof: Here ABCE is a cyclic quadrilateral
∠2+∠4=180° —–[sum of opposite is of a cyclic quadrilateral is 180°]
∠4=180°-∠1 ——-1
Now ∠4+∠6=180°-∠6 ———2
From 1 and 2
180°-∠2=∠180°-∠6
∠2=∠6 ———–3
Also ∠2=∠5 ———[opposite angles of ||gm are equal] —–4
From 3 and 4
∠5=∠6
Now, In ∆ADE,
∠5=∠6
∴AE=AD ——[sides apposite to equal angles in a∆ are equal]
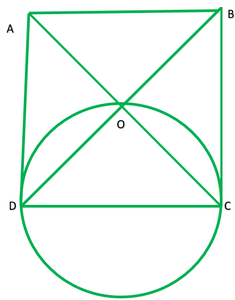
Question 7. AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
Solution:
Given: Two chords AC and BD bisects each other i.e OA=OC,OB=OD
To prove: In ∆AOB and COB
AO=CO ——-[given]
∠AOB=∠COD ——[vertically opposite angle]
OB=OD ——–[give]
∴∆AOB≅∆COB ——[s.s.s]
AB=CD ——[C.P.C.T.] 1
similarly ∆AOD≅∆COB (S.A.S)
AD=CD (C.P.C.T.) 2
From 1 and 2 ABCD is a ||gm
Since, ABCD is cyclic quadrilateral
∴∠A+∠C=180°
∠B+∠B=180°
2∠B=180°
∠B=180°/2
∠B=90°
∴ ∠A and ∠B lies in a semicircle
→ AC and BD are diameter of circle.
ii) Since ABCD is a ||gm and ∠A=90°
∴ ABCD is a rectangle.
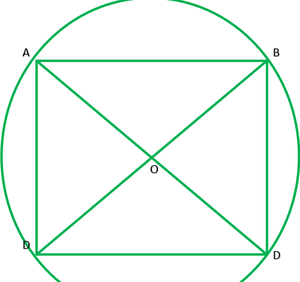
Question 8. Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – 1 2 A, 90° – 1 2 B and 90° – 1 2 C.
Solution:
Given:∆ABC and it circum-circle AD,BE and CF are bisectors of ∠A,∠B and ∠C
Respectively.
To proof:∠ D=90°-1/2∠A , ∠E=90°-1/2∠B , ∠F=90°-1/2∠C
Construction: Join AE and AF.
Solution: ∠ADE=∠ABE ———-1 [angle in the same segment are equal]
∠ADF=∠ACF ———–2 [angle in the same segment are equal]
Adding 1 and 2
∠ADE+∠ABF=∠ABE+∠ACF
∠D=1/2∠B+1/2∠C ——[BC and CF are bisector of ∠B & ∠c]
∠D=1/2(∠B+∠C)
∠D=1/2(180°-∠A)
∠D=1/2(180°-∠A)
∠D=90°-1/2∠AC
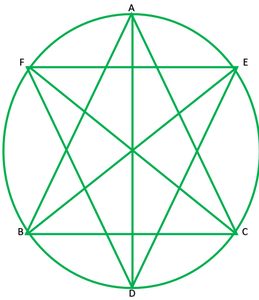
Question 9. Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution:
Given: two congruent circles which intersect at A and B.
PAB is a line segment
To prove: BA=BQ
Construction: join AB
Proof: AB is a common chord of both the congruent circle.
Segment of both circles will be equal
∠P=∠Q
Now, in ∆ BPQ,
∠P=∠Q
BP=BQ ——[sides opposite to equal angles are equal]
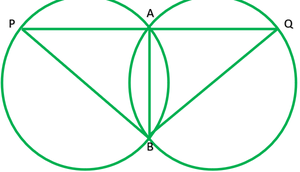
Question 10. In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Solution:
Given: A ∆ABC, in which AD is angle bisector of ∠A and OD is ⊥ bisector of BC.
To prove: D lies on circumcircle.
Construction: Join OB and OC
Proof: Since BC subtends ∠BAC at A on the remaining of the circle.
∠BOC=2∠BAC ——-1
Now, In ∆BOE and ∆ COE
BO=OE ——–(radii of the same circle)
BE=CE —–(give)
∴∆BOE≅COE ——-(S.S.S)
∠1=∠2 ——-(c.p.c.t)
Now,
∠1+∠2=∠BOC
2∠1=∠BOC
2∠1=2∠BAC ———- (from 1)
∠1=∠BAC
∠BOE=∠BAF
∠BOD=∠BAC
∠BOD=2∠BAD [AD is bisector of ∠BAC]
This is possible only if BD is chord of the circle.
D lies on the circle.
Important Points to Remember
- NCERT Solutions for Class 9 will help students to learn the solution for all the NCERT Problems.
- These solutions are entirely accurate and can be used by students to prepare for their board exams.
- All the solutions provided are in a step-by-step format for better understanding.
Key Takeaways of NCERT Solutions Class 9 Maths Chapter 10
By utilizing the class 9 questions with solutions on circles, students can reap various advantages that would aid their academic growth. Firstly, these comprehensive resources enable students to improve their scores significantly while simultaneously enhancing their understanding of the subject matter. Moreover, what further adds to their accessibility is the fact that these helpful PDF files are conveniently available free of charge. Therefore, students have the flexibility to choose between a soft copy or a hard copy, based on their personal preference and convenience.
Also Check:
FAQs – NCERT Solutions for Class 9 Maths Chapter 10 Circles
Q1: Why is it important to learn about Circles?
It is crucial to understand circles since they are fundamental geometric forms having numerous uses in a variety of industries, including math, physics, engineering, and architecture. Understanding circles enables you to apply ideas like tangents, chords, and sectors to solve issues involving their properties, such as calculating circumference, area, and arc length. In general, understanding circles is crucial for building a solid geometry foundation and for practical applications in a variety of fields.
Q2: What topics are covered in NCERT Solutions for Chapter 10- Circles?
NCERT Solutions for Class 9 Maths Chapter 10- Circles covers circles introduction and related terms and theorems related to circles.
Q3: How can NCERT Solutions for Class 9 Maths Chapter 10- Circles help me?
NCERT Solutions for Class 9 Maths Chapter 10- Circles can help you solve the NCERT exercise without any limitations. If you are stuck on a problem, you can find its solution in these solutions and free yourself from the frustration of being stuck on some question.
Q4: How many exercises are there in Class 9 Maths Chapter 10-Circles?
There are 6 exercises in the Class 9 Maths Chapter 10- Circles which covers all the important topics and sub-topics.
Q5: Where can I find NCERT Solutions for Class 9 Maths Chapter 10-Circles?
You can find these NCERT Solutions in this article created by our team of experts at GeeksforGeeks.
Q6: How are NCERT Solutions for Class 9 Maths Chapter 10 helpful for Class 9 students?
To excel in CBSE board exams, students often rely on NCERT textbooks as their primary study material. These textbooks are renowned for their comprehensive content, making them an invaluable resource. In order to enhance their understanding of the textbook problems, students can conveniently refer to the NCERT solutions for Class 9 Maths Chapter 10 offered by GeeksforGeeks. These solutions are meticulously prepared by experts, providing precise and accurate methods to solve the problems effectively. By utilizing these solutions, students can significantly boost their proficiency and master the subject in no time.
Share your thoughts in the comments
Please Login to comment...