Minimax Algorithm in Game Theory | Set 1 (Introduction)

Minimax is a kind of backtracking algorithm that is used in decision making and game theory to find the optimal move for a player, assuming that your opponent also plays optimally. It is widely used in two player turn-based games such as Tic-Tac-Toe, Backgammon, Mancala, Chess, etc.
In Minimax the two players are called maximizer and minimizer. The maximizer tries to get the highest score possible while the minimizer tries to do the opposite and get the lowest score possible.
Every board state has a value associated with it. In a given state if the maximizer has upper hand then, the score of the board will tend to be some positive value. If the minimizer has the upper hand in that board state then it will tend to be some negative value. The values of the board are calculated by some heuristics which are unique for every type of game.

Example:
Consider a game which has 4 final states and paths to reach final state are from root to 4 leaves of a perfect binary tree as shown below. Assume you are the maximizing player and you get the first chance to move, i.e., you are at the root and your opponent at next level. Which move you would make as a maximizing player considering that your opponent also plays optimally?

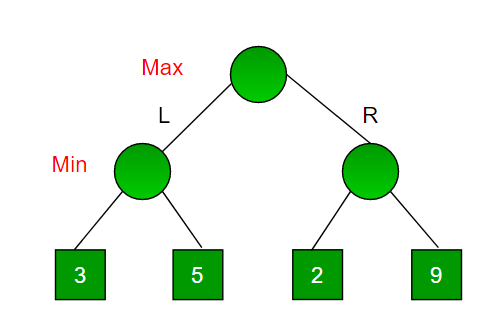
Since this is a backtracking based algorithm, it tries all possible moves, then backtracks and makes a decision. 

• Maximizer goes LEFT: It is now the minimizers turn. The minimizer now has a choice between 3 and 5. Being the minimizer it will definitely choose the least among both, that is 3
• Maximizer goes RIGHT: It is now the minimizers turn. The minimizer now has a choice between 2 and 9. He will choose 2 as it is the least among the two values.

Being the maximizer you would choose the larger value that is 3. Hence the optimal move for the maximizer is to go LEFT and the optimal value is 3.

Now the game tree looks like below :

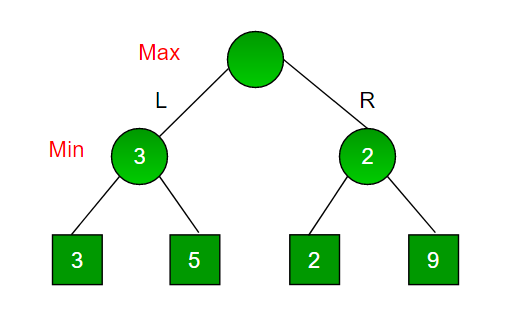
The above tree shows two possible scores when maximizer makes left and right moves.

Note: Even though there is a value of 9 on the right subtree, the minimizer will never pick that. We must always assume that our opponent plays optimally.

Below is the implementation for the same. 

C++

// A simple C++ program to find
// maximum score that
// maximizing player can get.
#include<bits/stdc++.h>
using namespace std;

// Returns the optimal value a maximizer can obtain.
// depth is current depth in game tree.
// nodeIndex is index of current node in scores[].
// isMax is true if current move is
// of maximizer, else false
// scores[] stores leaves of Game tree.
// h is maximum height of Game tree
int minimax(int depth, int nodeIndex, bool isMax,
            int scores[], int h)
{
    // Terminating condition. i.e
    // leaf node is reached
    if (depth == h)
        return scores[nodeIndex];

    //  If current move is maximizer,
    // find the maximum attainable
    // value
    if (isMax)
       return max(minimax(depth+1, nodeIndex*2, false, scores, h),
            minimax(depth+1, nodeIndex*2 + 1, false, scores, h));

    // Else (If current move is Minimizer), find the minimum
    // attainable value
    else
        return min(minimax(depth+1, nodeIndex*2, true, scores, h),
            minimax(depth+1, nodeIndex*2 + 1, true, scores, h));
}

// A utility function to find Log n in base 2
int log2(int n)
{
  return (n==1)? 0 : 1 + log2(n/2);
}

// Driver code
int main()
{
    // The number of elements in scores must be
    // a power of 2.
    int scores[] = {3, 5, 2, 9, 12, 5, 23, 23};
    int n = sizeof(scores)/sizeof(scores[0]);
    int h = log2(n);
    int res = minimax(0, 0, true, scores, h);
    cout << "The optimal value is : " << res << endl;
    return 0;
}

Java

// A simple java program to find maximum score that
// maximizing player can get.

import java.io.*;

class GFG {


// Returns the optimal value a maximizer can obtain.
// depth is current depth in game tree.
// nodeIndex is index of current node in scores[].
// isMax is true if current move is of maximizer, else false
// scores[] stores leaves of Game tree.
// h is maximum height of Game tree
 static int minimax(int depth, int nodeIndex, boolean  isMax,
            int scores[], int h)
{
    // Terminating condition. i.e leaf node is reached
    if (depth == h)
        return scores[nodeIndex];

    // If current move is maximizer, find the maximum attainable
    // value
    if (isMax)
    return Math.max(minimax(depth+1, nodeIndex*2, false, scores, h),
            minimax(depth+1, nodeIndex*2 + 1, false, scores, h));

    // Else (If current move is Minimizer), find the minimum
    // attainable value
    else
        return Math.min(minimax(depth+1, nodeIndex*2, true, scores, h),
            minimax(depth+1, nodeIndex*2 + 1, true, scores, h));
}

// A utility function to find Log n in base 2
 static int log2(int n)
{
return (n==1)? 0 : 1 + log2(n/2);
}

// Driver code

    public static void main (String[] args) {
            // The number of elements in scores must be
    // a power of 2.
    int scores[] = {3, 5, 2, 9, 12, 5, 23, 23};
    int n = scores.length;
    int h = log2(n);
    int res = minimax(0, 0, true, scores, h);
    System.out.println( "The optimal value is : "  +res);

    }
}

// This code is contributed by vt_m

C#

// A simple C# program to find maximum score that
// maximizing player can get.
using System;

public class GFG
{

// Returns the optimal value a maximizer can obtain.
// depth is current depth in game tree.
// nodeIndex is index of current node in scores[].
// isMax is true if current move is of maximizer, else false
// scores[] stores leaves of Game tree.
// h is maximum height of Game tree
static int minimax(int depth, int nodeIndex, bool isMax,
            int []scores, int h)
{
    // Terminating condition. i.e leaf node is reached
    if (depth == h)
        return scores[nodeIndex];

    // If current move is maximizer, find the maximum attainable
    // value
    if (isMax)
    return Math.Max(minimax(depth+1, nodeIndex*2, false, scores, h),
            minimax(depth+1, nodeIndex*2 + 1, false, scores, h));

    // Else (If current move is Minimizer), find the minimum
    // attainable value
    else
        return Math.Min(minimax(depth+1, nodeIndex*2, true, scores, h),
            minimax(depth+1, nodeIndex*2 + 1, true, scores, h));
}

// A utility function to find Log n in base 2
static int log2(int n)
{
    return (n==1)? 0 : 1 + log2(n/2);
}

// Driver code
static public void Main ()
{

    // The number of elements in scores must be
    // a power of 2.
    int []scores = {3, 5, 2, 9, 12, 5, 23, 23};
    int n = scores.Length;
    int h = log2(n);
    int res = minimax(0, 0, true, scores, h);
    Console.WriteLine( "The optimal value is : " +res);

}
}

// This code is contributed by ajit.

Python3

# A simple Python3 program to find
# maximum score that
# maximizing player can get
import math

def minimax (curDepth, nodeIndex,
             maxTurn, scores,
             targetDepth):

    # base case : targetDepth reached
    if (curDepth == targetDepth):
        return scores[nodeIndex]

    if (maxTurn):
        return max(minimax(curDepth + 1, nodeIndex * 2,
                    False, scores, targetDepth),
                   minimax(curDepth + 1, nodeIndex * 2 + 1,
                    False, scores, targetDepth))

    else:
        return min(minimax(curDepth + 1, nodeIndex * 2,
                     True, scores, targetDepth),
                   minimax(curDepth + 1, nodeIndex * 2 + 1,
                     True, scores, targetDepth))

# Driver code
scores = [3, 5, 2, 9, 12, 5, 23, 23]

treeDepth = math.log(len(scores), 2)

print("The optimal value is : ", end = "")
print(minimax(0, 0, True, scores, treeDepth))

# This code is contributed
# by rootshadow

Javascript

<script>

// Javascript program to find maximum score that
// maximizing player can get.

// Returns the optimal value a maximizer can obtain.
// depth is current depth in game tree.
// nodeIndex is index of current node in scores[].
// isMax is true if current move is of maximizer, else false
// scores[] stores leaves of Game tree.
// h is maximum height of Game tree
 function minimax(depth, nodeIndex, isMax,
            scores, h)
{
    // Terminating condition. i.e leaf node is reached
    if (depth == h)
        return scores[nodeIndex];

    // If current move is maximizer, find the maximum attainable
    // value
    if (isMax)
    return Math.max(minimax(depth+1, nodeIndex*2, false, scores, h),
            minimax(depth+1, nodeIndex*2 + 1, false, scores, h));

    // Else (If current move is Minimizer), find the minimum
    // attainable value
    else
        return Math.min(minimax(depth+1, nodeIndex*2, true, scores, h),
            minimax(depth+1, nodeIndex*2 + 1, true, scores, h));
}

// A utility function to find Log n in base 2
 function log2(n)
{
return (n==1)? 0 : 1 + log2(n/2);
}


// Driver Code

    // The number of elements in scores must be
    // a power of 2.
    let scores = [3, 5, 2, 9, 12, 5, 23, 23];
    let n = scores.length;
    let h = log2(n);
    let res = minimax(0, 0, true, scores, h);
    document.write( "The optimal value is : "  +res);


</script>

Output:

The optimal value is:  12

Time complexity : O(b^d) b is the branching factor and d is count of depth or ply of graph or tree.

Space Complexity : O(bd) where b is branching factor into d is maximum depth of tree similar to DFS.

The idea of this article is to introduce Minimax with a simple example. 

• In the above example, there are only two choices for a player. In general, there can be more choices. In that case, we need to recur for all possible moves and find the maximum/minimum. For example, in Tic-Tac-Toe, the first player can make 9 possible moves.
• In the above example, the scores (leaves of Game Tree) are given to us. For a typical game, we need to derive these values

We will soon be covering Tic Tac Toe with Minimax algorithm.
This article is contributed by Akshay L. Aradhya. If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above