You must have heard some advertisements regarding medical insurance that promises to help financially in case of any medical emergency. One who purchases this type of insurance has to pay premiums monthly and this premium amount varies vastly depending upon various factors.

Medical Insurance Price Prediction using Machine Learning in Python
In this article, we will try to extract some insights from a dataset that contains details about the background of a person who is purchasing medical insurance along with what amount of premium is charged to those individuals as well using Machine Learning in Python.
Importing Libraries and Dataset
Python libraries make it very easy for us to handle the data and perform typical and complex tasks with a single line of code.
- Pandas – This library helps to load the data frame in a 2D array format and has multiple functions to perform analysis tasks in one go.
- Numpy – Numpy arrays are very fast and can perform large computations in a very short time.
- Matplotlib/Seaborn – This library is used to draw visualizations.
Python3
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib as pt
import warnings
warnings.filterwarnings("ignore")
|
Now let’s use the panda’s data frame to load the dataset and look at the first five rows of it.
Python3
df=pd.read_csv("insurance.csv")
df
|
Output:

Data Set
Now, we can observe the data and its shape(rows x columns)
This dataset contains 1338 data points with 6 independent features and 1 target feature(charges).
Output:
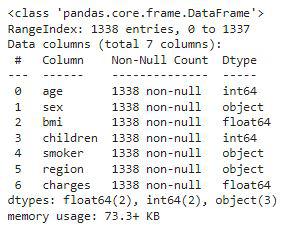
Details about the columns of the dataset
From the above, we can see that the dataset contains 2 columns with float values 3 with categorical values and the rest contains integer values.
Output:
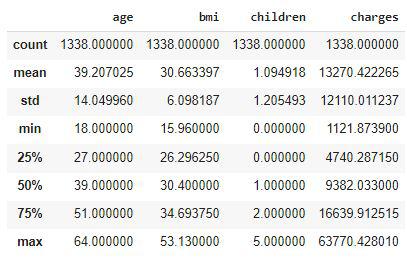
Descriptive Statistical measures of the data
We can look at the descriptive statistical measures of the continuous data available in the dataset.
Exploratory Data Analysis
EDA is an approach to analyzing the data using visual techniques. It is used to discover trends, and patterns, or to check assumptions with the help of statistical summaries and graphical representations. While performing the EDA of this dataset we will try to look at what is the relation between the independent features that is how one affects the other.
Output:
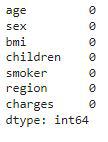
Count of the null values column wise
So, here we can conclude that there are no null values in the dataset given.
Python3
features = ['sex', 'smoker', 'region']
plt.subplots(figsize=(20, 10))
for i, col in enumerate(features):
plt.subplot(1, 3, i + 1)
x = df[col].value_counts()
plt.pie(x.values,
labels=x.index,
autopct='%1.1f%%')
plt.show()
|
Output:
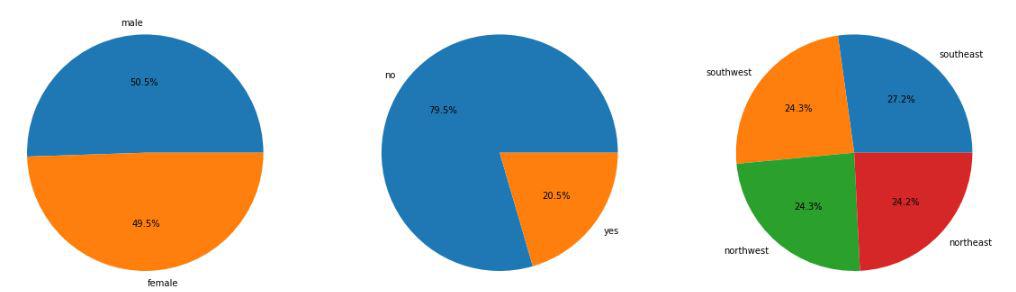
Pie chart for the sex, smoker, and region column
The data provided to us is equally distributed among the sex and the region columns but in the smoker column, we can observe a ratio of 80:20.
Python3
features = ['sex', 'children', 'smoker', 'region']
plt.subplots(figsize=(20, 10))
for i, col in enumerate(features):
plt.subplot(2, 2, i + 1)
df.groupby(col).mean()['charges'].plot.bar()
plt.show()
|
Output:
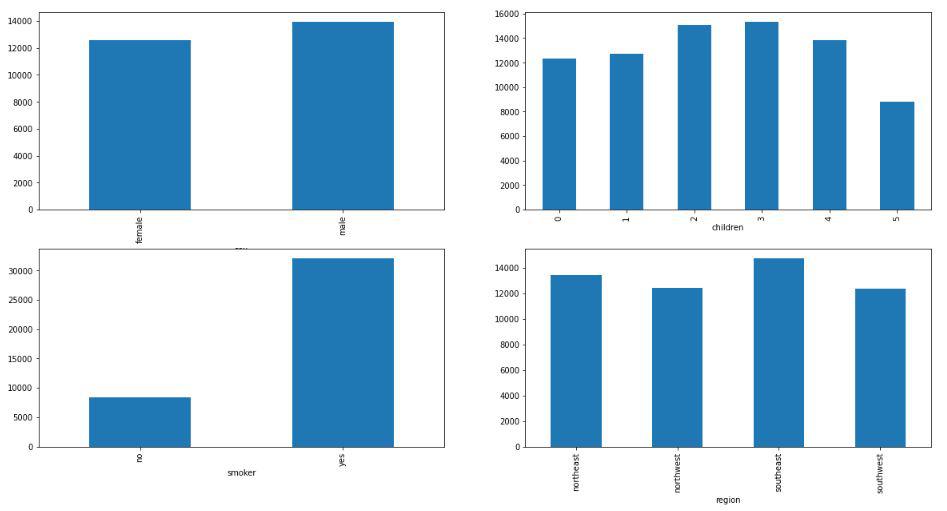
Comparison between charges paid between different groups
Now let’s look at some of the observations which are shown in the above graphs:
- Charges are on the higher side for males as compared to females but the difference is not that much.
- Premium charged from the smoker is around thrice that which is charged from non-smokers.
- Charges are approximately the same in the given four regions.
Python3
features = ['age', 'bmi']
plt.subplots(figsize=(17, 7))
for i, col in enumerate(features):
plt.subplot(1, 2, i + 1)
sb.scatterplot(data=df, x=col,
y='charges',
hue='smoker')
plt.show()
|
Output:
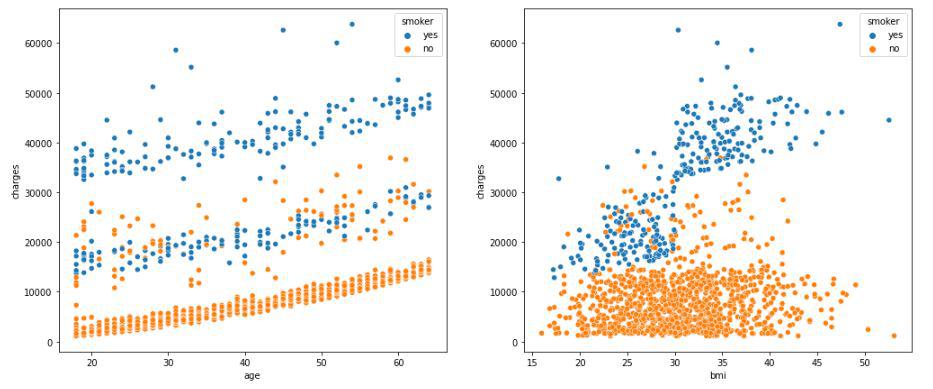
Scatter plot of the charges paid v/s age and BMI respectively
A clear distinction can be observed here between the charges that smokers have to pay. Also here as well we can observe that as the age of a person increases premium prices goes up as well.
DATA PREPROCESSING
Data preprocessing is technique to clean the unusual data like the missing values,wrong data,wrong format of data,duplicated data and the outliers.In this data we can observe that there are no missing values and wrong data.The only thing we can need to check is for duplicates and presence of outliers.
Python3
df.drop_duplicates(inplace=True)
sns.boxplot(df['age'])
|
Output:

Boxplot of age
we can see that there are no outliers present in age column

Box plot of bmi
Due to the presence of outliers present in bmi column we need to treat the outliers by replacing the values with mean as the bmi column consists of continuous data.
Python3
Q1=df['bmi'].quantile(0.25)
Q2=df['bmi'].quantile(0.5)
Q3=df['bmi'].quantile(0.75)
iqr=Q3-Q1
lowlim=Q1-1.5*iqr
upplim=Q3+1.5*iqr
print(lowlim)
print(upplim)
|
Output:
13.674999999999994
47.31500000000001
Python3
from feature_engine.outliers import ArbitraryOutlierCapper
arb=ArbitraryOutlierCapper(min_capping_dict={'bmi':13.6749},max_capping_dict={'bmi':47.315})
df[['bmi']]=arb.fit_transform(df[['bmi']])
sns.boxplot(df['bmi'])
|
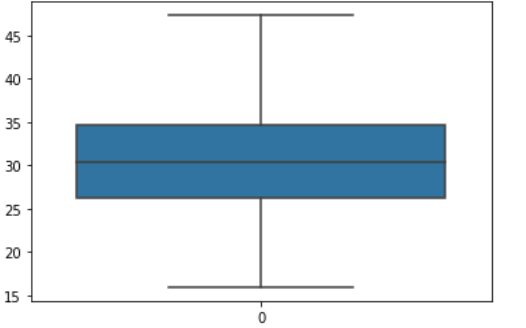
Box plot for bmi
Now we successfully treated the outliers .
Data Wrangling
Data wrangling is a technique to ensure whether the data follow normal or standard distribution and encode the discrete data for prediction.
Python3
df['bmi'].skew()
df['age'].skew()
|
Output:
0.23289153320569975
0.054780773126998195
Data in both the age and BMI column approximately follow a Normal distribution which is a good point with respect to the model’s learning.
Encoding
encoding is to be done for discrete categorical data (sex,bmi,region).
Python3
df['sex']=df['sex'].map({'male':0,'female':1})
df['smoker']=df['smoker'].map({'yes':1,'no':0})
df['region']=df['region'].map({'northwest':0, 'northeast':1,'southeast':2,'southwest':3})
|
Output:

Encoded Data
Now the discrete data is encoded and the data preprocessing and data wrangling part is completed.Now we can go for model development.
Output:

correlation matrix
Model Development
There are so many state-of-the-art ML models available in academia but some model fits better to some problem while some fit better than other. So, to make this decision we split our data into training and validation data. Then we use the validation data to choose the model with the highest performance.
Python3
X=df.drop(['charges'],axis=1)
Y=df[['charges']]
from sklearn.linear_model import LinearRegression,Lasso
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from xgboost import XGBRegressor
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
l1=[]
l2=[]
l3=[]
cvs=0
for i in range(40,50):
xtrain,xtest,ytrain,ytest=train_test_split(X,Y,test_size=0.2,random_state=i)
lrmodel=LinearRegression()
lrmodel.fit(xtrain,ytrain)
l1.append(lrmodel.score(xtrain,ytrain))
l2.append(lrmodel.score(xtest,ytest))
cvs=(cross_val_score(lrmodel,X,Y,cv=5,)).mean()
l3.append(cvs)
df1=pd.DataFrame({'train acc':l1,'test acc':l2,'cvs':l3})
df1
|
Output:
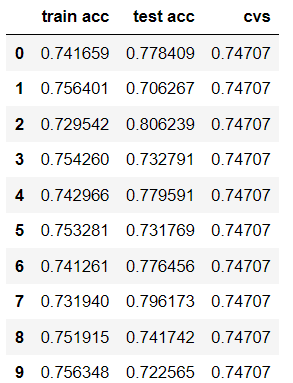
Scores for various random_state number
After dividing the data into training and validation data it is considered a better practice to achieve stable and fast training of the model.We have identified the best random_state number for this data set as 42 .Now we fix this random_state and try with different ml algorithms for better score or accuracy.
Now let’s train some state-of-the-art machine learning models on the training data and then use the validation data for choosing the best out of them for prediction.
Python3
xtrain,xtest,ytrain,ytest=train_test_split(X,Y,test_size=0.2,random_state=42)
lrmodel=LinearRegression()
lrmodel.fit(xtrain,ytrain)
print(lrmodel.score(xtrain,ytrain))
print(lrmodel.score(xtest,ytest))
print(cross_val_score(lrmodel,X,Y,cv=5,).mean())
|
Output:
Linear Regression:
0.7295415541376445
0.8062391115570589
0.7470697972809902
Python3
from sklearn.metrics import r2_score
svrmodel=SVR()
svrmodel.fit(xtrain,ytrain)
ypredtrain1=svrmodel.predict(xtrain)
ypredtest1=svrmodel.predict(xtest)
print(r2_score(ytrain,ypredtrain1))
print(r2_score(ytest,ypredtest1))
print(cross_val_score(svrmodel,X,Y,cv=5,).mean())
|
Output:
SVR:
-0.10151474302536445
-0.1344454720199666
-0.10374591327267262
Python3
rfmodel=RandomForestRegressor(random_state=42)
rfmodel.fit(xtrain,ytrain)
ypredtrain2=rfmodel.predict(xtrain)
ypredtest2=rfmodel.predict(xtest)
print(r2_score(ytrain,ypredtrain2))
print(r2_score(ytest,ypredtest2))
print(cross_val_score(rfmodel,X,Y,cv=5,).mean())
from sklearn.model_selection import GridSearchCV
estimator=RandomForestRegressor(random_state=42)
param_grid={'n_estimators':[10,40,50,98,100,120,150]}
grid=GridSearchCV(estimator,param_grid,scoring="r2",cv=5)
grid.fit(xtrain,ytrain)
print(grid.best_params_)
rfmodel=RandomForestRegressor(random_state=42,n_estimators=120)
rfmodel.fit(xtrain,ytrain)
ypredtrain2=rfmodel.predict(xtrain)
ypredtest2=rfmodel.predict(xtest)
print(r2_score(ytrain,ypredtrain2))
print(r2_score(ytest,ypredtest2))
print(cross_val_score(rfmodel,X,Y,cv=5,).mean())
|
Output:
RandomForestRegressor:
0.9738163260247533
0.8819423353068565
0.8363637309718952
Hyperparametertuning:
{'n_estimators': 120}
0.9746383984429655
0.8822009842175969
0.8367438097052858
Python3
gbmodel=GradientBoostingRegressor()
gbmodel.fit(xtrain,ytrain)
ypredtrain3=gbmodel.predict(xtrain)
ypredtest3=gbmodel.predict(xtest)
print(r2_score(ytrain,ypredtrain3))
print(r2_score(ytest,ypredtest3))
print(cross_val_score(gbmodel,X,Y,cv=5,).mean())
from sklearn.model_selection import GridSearchCV
estimator=GradientBoostingRegressor()
param_grid={'n_estimators':[10,15,19,20,21,50],'learning_rate':[0.1,0.19,0.2,0.21,0.8,1]}
grid=GridSearchCV(estimator,param_grid,scoring="r2",cv=5)
grid.fit(xtrain,ytrain)
print(grid.best_params_)
gbmodel=GradientBoostingRegressor(n_estimators=19,learning_rate=0.2)
gbmodel.fit(xtrain,ytrain)
ypredtrain3=gbmodel.predict(xtrain)
ypredtest3=gbmodel.predict(xtest)
print(r2_score(ytrain,ypredtrain3))
print(r2_score(ytest,ypredtest3))
print(cross_val_score(gbmodel,X,Y,cv=5,).mean())
|
Output:
GradientBoostingRegressor:
0.8931345821166041
0.904261922040551
0.8549940291799407
Hyperparametertuning
{'learning_rate': 0.2, 'n_estimators': 21}
0.8682397447116927
0.9017109716082661
0.8606041910125791
Python3
xgmodel=XGBRegressor()
xgmodel.fit(xtrain,ytrain)
ypredtrain4=xgmodel.predict(xtrain)
ypredtest4=xgmodel.predict(xtest)
print(r2_score(ytrain,ypredtrain4))
print(r2_score(ytest,ypredtest4))
print(cross_val_score(xgmodel,X,Y,cv=5,).mean())
from sklearn.model_selection import GridSearchCV
estimator=XGBRegressor()
param_grid={'n_estimators':[10,15,20,40,50],'max_depth':[3,4,5],'gamma':[0,0.15,0.3,0.5,1]}
grid=GridSearchCV(estimator,param_grid,scoring="r2",cv=5)
grid.fit(xtrain,ytrain)
print(grid.best_params_)
xgmodel=XGBRegressor(n_estimators=15,max_depth=3,gamma=0)
xgmodel.fit(xtrain,ytrain)
ypredtrain4=xgmodel.predict(xtrain)
ypredtest4=xgmodel.predict(xtest)
print(r2_score(ytrain,ypredtrain4))
print(r2_score(ytest,ypredtest4))
print(cross_val_score(xgmodel,X,Y,cv=5,).mean())
|
Output:
XGBRegressor:
0.9944530188818493
0.8618686915522016
0.8104424308304893
Hyperparametertuning:
{'gamma': 0, 'max_depth': 3, 'n_estimators': 15}
0.870691899927822
0.904151903449132
0.8600710679082143
Comapring All Models
|
Train Accuracy
|
Test Accuracy
|
CV Score
|
|
-0.105
|
-0.134
|
0.103
|
|
0.974
|
0.882
|
0.836
|
|
0.868
|
0.901
|
0.860
|
|
0.870
|
0.904
|
0.860
|
From the above table we can observe that XGBoost is the best model.Now we need to identify the important features for predicting of charges.
Python3
feats=pd.DataFrame(data=grid.best_estimator_.feature_importances_,index=X.columns,columns=['Importance'])
feats
|
Output:

Features Importance
Python3
important_features=feats[feats['Importance']>0.01]
important_features
|
Output:

Important Features
Final Model:
Python3
df.drop(df[['sex','region']],axis=1,inplace=True)
Xf=df.drop(df[['charges']],axis=1)
X=df.drop(df[['charges']],axis=1)
xtrain,xtest,ytrain,ytest=train_test_split(Xf,Y,test_size=0.2,random_state=42)
finalmodel=XGBRegressor(n_estimators=15,max_depth=3,gamma=0)
finalmodel.fit(xtrain,ytrain)
ypredtrain4=finalmodel.predict(xtrain)
ypredtest4=finalmodel.predict(xtest)
print(r2_score(ytrain,ypredtrain4))
print(r2_score(ytest,ypredtest4))
print(cross_val_score(finalmodel,X,Y,cv=5,).mean())
|
Final Model:
Train accuracy : 0.870691899927822
Test accuracy : 0.904151903449132
CV Score : 0.8600710679082143
Save Model:
Python3
from pickle import dump
dump(finalmodel,open('insurancemodelf.pkl','wb'))
|
Predict on new data:
Python3
new_data=pd.DataFrame({'age':19,'sex':'male','bmi':27.9,'children':0,'smoker':'yes','region':'northeast'},index=[0])
new_data['smoker']=new_data['smoker'].map({'yes':1,'no':0})
new_data=new_data.drop(new_data[['sex','region']],axis=1)
finalmodel.predict(new_data)
|
Output:
array([17483.12], dtype=float32
Conclusion
Out of all the models XGBoost model is giving the highest accuracy this means predictions made by this model are close to the real values as compared to the other model.
The dataset we have used here was small still the conclusion we drew from them were quite similar to what is observed in the real-life scenario. If we would have a bigger dataset then we will be able to learn even deeper patterns in the relation between the independent features and the premium charged from the buyers.
Share your thoughts in the comments
Please Login to comment...