When Humans look at their childhood pictures, the first thing they realize is how tall or heavy they have become as compared to the early stages of their lives. Noticing the increment in the weight or becoming taller is done through measurement. Measurement is required everywhere in order to specifically compare a quantity’s value from its original value. There can be many examples where measurement is required, For example, a thermometer is used to measure the temperature in Celsius of the body, the clocks on the wall are used to measure time in hours, and so on.
Measurement
Calculating the value of one quantity by comparing it with the standard value of the same physical quantity is called Measurement. It can be said that measurement associates the physical quantity with its numeric value.
Normally, objects are measured by placing them next to each other, and it can be explained which one is heavier or taller, etc. Measuring an object gives two results- value and unit of the quantity. For example, The length of the scale is 15 cm long where 15 is the value and the centimeter is the unit used for length.
Metric System
Metric system is the system that came from the decimal system and this system is used to measure basic quantities, metric system paves the way for the conversion of units, that is, the conversion of bigger units into smaller and vice-versa is possible due to the system. The basic quantities that are present are meter, gram, and liters, and they are used to measuring quantities of length, volume/mass, and capacity.
Measurement of Length
According to the metric system, length is calculated in meters. However, it can easily be converted into other forms depending upon the requirement, for instance, if the requirement is to measure the bigger quantity, it should be measured in kilometers, if the requirement is to measure something smaller, it should be in centimeters. Let’s say, the requirement is to measure a certain distance, it should either be in meters or kilometers.

Below is the easier way to explain the conversion,


Measurement of Area
In the standard way, the area of any quantity is measured in meter2, since the area is a two-dimensional quantity that is scalar in nature. It involves lengths going in two different directions known as length and breadth. The area of bigger and smaller quantities can be converted easily using different units, for example, if the area of a small table is to be measured, it is measured in cm2 and if the area of the plot is to be measured, the unit used is meter2.

Below is the easier way to explain the conversion,

Measurement of Volume
The volume of any quantity is three-dimensional in nature, that is, the length if going in three directions, unlike length or area, the volume contains capacity. The standard unit used to measure volume is meter3. The unit is converted into bigger and smaller units like decimeter3 or kilometer3 based on how big or small the quantity is, it is done by simply dividing/ multiplying by tens, hundreds, thousands, and so on.

Below is the easier way to explain the conversion,

Measurement of Density
The density of any object is defined as the mass of that object per unit volume. Density tells how close or far away molecules are packed in a certain volume. The very famous scientist known as Archimedes discovered the concept of the Density of an object. In the metric system, Density is measured in kg/m3 and is represented as D or ρ. Therefore, it can be denoted as,
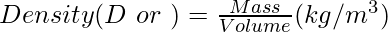
Note:
- Density has big significance in real life. One example to prove the same is the concept of an object floating on water, The density of any object helps in identifying whether an object can float on water or not. If the density of the object is lesser than that of water (997.7 kg/m3), it will float on water.
- The SI unit of density is kg/m3, but for measurement of solids, g/cm3 can also be used. In order to measure the density of liquids, mostly g/ml is used.
Sample Problems
Question 1: Convert the following: m3 to mm3, liter to meter3, mile3 to km3.
Solution:
The conversion of the above-mentioned quantities are as follows,
1 meter = 1000 millimeters
1m3= 1000 × 1000 × 1000 mm3
Therefore, 1m3 = 1 × 109 m3.
It is known that 1 meter3 = 1000 liters
By unitary method, 1 liters = 1/1000 m3
1 liter= 1 × 10-3 m3.
1 mile = 1.609 km
1 mile3 = 1.609 × 1.609 × 1.609 km3
1 mile3 = 4.165 km3
Question 2: What is the difference between the metric system and the imperial system of measurement?
Answer:
Difference between metric system and imperial system,
| Metric system | Imperial system |
| Known as International systems of units | Known as British imperial system |
| Measurement is done in Meter, gram and liter | Measurement is done in feet, pound, inches |
| Simple conversion (used by 95% of population currently) | Complex conversion |
Question 3: Calculate the density of an object having a mass of 1200kg and its volume is 10m3.
Solution:
Density of an object is given as,
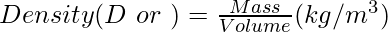
D = 1200/10 kg/m3
D = 120 kg/m3.
Question 4: There are two large boxes filled with biscuits. The first has 10 biscuits and the second has 20 biscuit packets present in it. The box have the same volume. Explain which box will weigh more?
Answer:
The concept is based on density. Density of an object is defined as mass/volume. Here, both the boxes have equal volume but the mass of the second box is more as it contain twice as many biscuits as first box. Hence, the second box will weigh more.
Question 5: A cube is given which has a volume of 1000m3. Calculate the surface area of the cube in cm3.
Solution:
The surface area of a cube = 6a2
where a is the length if the side of cube
Given, Volume of cube= 1000m3 =a3
a = 10meter
Surface area (in meter2) = 6 × 102 = 600meter2
1 meter= 100 centimeter
1 m2= 100 × 100 cm2
Therefore, Surface area of the cube= 600 × 104 cm2.
Question 6: The length and the breadth of a cuboid are same, but the height is twice in value. If the volume of the cuboid is 54000m3, find the length, breadth and height of the cuboid in centimeters.
Solution:
Volume of a cuboid = L × B × H= 54000m3
Let the length and breadth be z, then the height will be 2z
2z × z× z= 54000
2z3= 54000
z3= 27000
z= 30m
Length= 30m, Breadth= 30m, Height = 60m
In centimeters, Length= 30× 100= 3000cm
Breadth = 30 × 100= 3000cm
Height= 60 × 1000= 6000cm
Question 7: A cm scale has a limit of 15 points, how long is the scale in meters?
Solution:
Converting cm scale into m scale,
1 cm = 10-2m
15 cm = 0.15m
Hence, a 15cm long scale has a length of 0.15m in International System of Units.
Share your thoughts in the comments
Please Login to comment...