Side of a regular n-sided polygon circumscribed in a circle

Given two integers r and n where n is the number of sides of a regular polygon and r is the radius of the circle this polygon is circumscribed in. The task is to find the length of the side of polygon. 

Examples:

Input: n = 5, r = 11 
Output: 12.9256
Input: n = 3, r = 5 
Output: 8.6576 

Approach: Consider the image above and let angle AOB be theta then theta = 360 / n. 
In right angled triangle 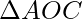, angle ACO = 90 degrees and angle AOC = theta / 2. 
So, AC = OA * sin(theta / 2) = r * sin(theta / 2)
Therefore, side of the polygon, AB = 2 * AC i.e. 2 * r * sin(theta / 2).

Below is the implementation of the above approach: 

C++

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;

// Function to calculate the side of the polygon
// circumscribed in a circle
float calculateSide(float n, float r)
{
    float theta, theta_in_radians;

    theta = 360 / n;
    theta_in_radians = theta * 3.14 / 180;

    return 2 * r * sin(theta_in_radians / 2);
}

// Driver Code
int main()
{

    // Total sides of the polygon
    float n = 3;

    // Radius of the circumscribing circle
    float r = 5;

    cout << calculateSide(n, r);
}

Java

// Java  implementation of the approach
import java.lang.Math;
import java.io.*;

class GFG {

// Function to calculate the side of the polygon
// circumscribed in a circle
static double calculateSide(double  n, double r)
{
    double theta, theta_in_radians;

    theta = 360 / n;
    theta_in_radians = theta * 3.14 / 180;

    return 2 * r * Math.sin(theta_in_radians / 2);
}

// Driver Code
    public static void main (String[] args) {

    // Total sides of the polygon
    double n = 3;

    // Radius of the circumscribing circle
    double r = 5;
    System.out.println (calculateSide(n, r));
    }
//This code is contributed by akt_mit
}

Python3

# Python 3 implementation of the approach
from math import sin

# Function to calculate the side of
# the polygon circumscribed in a circle
def calculateSide(n, r):
    theta = 360 / n
    theta_in_radians = theta * 3.14 / 180

    return 2 * r * sin(theta_in_radians / 2)

# Driver Code
if __name__ == '__main__':

    # Total sides of the polygon
    n = 3

    # Radius of the circumscribing circle
    r = 5

    print('{0:.5}'.format(calculateSide(n, r)))

# This code is contributed by
# Sanjit_Prasad

C#

// C# implementation of the approach

using System;

class GFG {

    // Function to calculate the side of the polygon
    // circumscribed in a circle
    static double calculateSide(double n, double r)
    {
        double theta, theta_in_radians;

        theta = 360 / n;
        theta_in_radians = theta * 3.14 / 180;

        return Math.Round(2 * r * Math.Sin(theta_in_radians / 2),4);
    }

        // Driver Code
    public static void Main () {

    // Total sides of the polygon
    double n = 3;

    // Radius of the circumscribing circle
    double r = 5;

    Console.WriteLine(calculateSide(n, r));
    }
    // This code is contributed by Ryuga
}

PHP

<?php
// PHP implementation of the approach

// Function to calculate the side of the
// polygon circumscribed in a circle
function calculateSide($n, $r)
{
    $theta; $theta_in_radians;

    $theta = 360 / $n;
    $theta_in_radians = $theta * 3.14 / 180;

    return 2 * $r * sin($theta_in_radians / 2);
}

// Driver Code

// Total sides of the polygon
$n = 3;

// Radius of the circumscribing circle
$r = 5;

echo calculateSide($n, $r);

// This code is contributed by inder_verma..
?>

Javascript

<script>

// javascript  implementation of the approach


// Function to calculate the side of the polygon
// circumscribed in a circle
function calculateSide( n , r)
{
    var theta, theta_in_radians;

    theta = 360 / n;
    theta_in_radians = theta * 3.14 / 180;

    return 2 * r * Math.sin(theta_in_radians / 2);
}

// Driver Code

// Total sides of the polygon
var n = 3;

// Radius of the circumscribing circle
var r = 5;
document.write(calculateSide(n, r).toFixed(5));

// This code contributed by Princi Singh

</script>

Output

8.6576

Time Complexity: O(1), since there is no loop or recursion.
Auxiliary Space: O(1), since no extra space has been taken.