Area of largest triangle that can be inscribed within a rectangle
Last Updated :
28 Aug, 2022
Given a rectangle of length 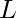 and breadth
and breadth 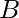 . The task is to find the area of the biggest triangle that can be inscribed in it.
. The task is to find the area of the biggest triangle that can be inscribed in it.
Examples:
Input: L = 5, B = 4
Output: 10
Input: L = 3, B = 2
Output: 3

From the figure, it is clear that the largest triangle that can be inscribed in the rectangle, should stand on the same base & has height raising between the same parallel sides of the rectangle.
So, the base of the triangle = B
Height of the triangle = L
Therefore Area,
A = (L*B)/2
Note: It should also be clear that if base of the triangle = diagonal of rectangle, still the area of triangle so obtained = lb/2 as diagonal of a rectangle divides it into 2 triangles of equal area.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float trianglearea(float l, float b)
{
if (l < 0 || b < 0)
return -1;
float area = (l * b) / 2;
return area;
}
int main()
{
float l = 5, b = 4;
cout << trianglearea(l, b) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static float trianglearea(float l, float b)
{
if (l < 0 || b < 0)
return -1;
float area = (l * b) / 2;
return area;
}
public static void main(String args[])
{
float l = 5, b = 4;
System.out.println(trianglearea(l, b));
}
}
|
Python3
def trianglearea(l, b) :
if (l < 0 or b < 0) :
return -1
area = (l * b) / 2
return area
l = 5
b = 4
print(trianglearea(l, b))
|
C#
using System;
class GFG
{
static float trianglearea(float l,
float b)
{
if (l < 0 || b < 0)
return -1;
float area = (l * b) / 2;
return area;
}
public static void Main()
{
float l = 5, b = 4;
Console.WriteLine(trianglearea(l, b));
}
}
|
PHP
<?php
function trianglearea($l, $b)
{
if ($l < 0 or $b < 0)
return -1;
$area = ($l * $b) / 2;
return $area;
}
$l = 5; $b = 4;
echo trianglearea($l, $b);
?>
|
Javascript
<script>
function trianglearea( l, b)
{
if (l < 0 || b < 0)
return -1;
let area = (l * b) / 2;
return area;
}
let l = 5, b = 4;
document.write( trianglearea(l, b) );
</script>
|
Time Complexity: O(1) since performing constant operations
Auxiliary Space: O(1), since no extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...