Minimum volume of cone that can be circumscribed about a sphere of radius R
Last Updated :
07 Aug, 2022
Given a sphere of radius R, The task is to find out the minimum volume of the cone that can be circumscribed about it.

Examples:
Input: R = 10
Output: Volume of cone = 8373.33
Explanation:
Radius of cone = 14.14 and Height of cone = 40,
Volume of cone = 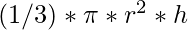 So, volume = 8373.33Input: R = 4 Output: Volume of cone = 535.89
So, volume = 8373.33Input: R = 4 Output: Volume of cone = 535.89
Approach:
we have given a sphere of radius R inscribed in Cone. We need to find out the radius and height of the cone to find out the volume of the cone.
In triangle AOE and ALC compute sin(X) i.e. For triangle AOE 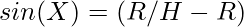 and for triangle ALC
and for triangle ALC 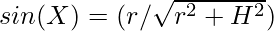
Now, From equating both we get 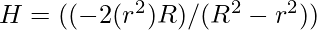
Insert the value of H in Volume i.e. 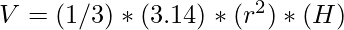 and for volume to be minimum
and for volume to be minimum 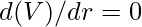 .
.
From the above equation we get 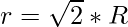 and putting this value in H we get
and putting this value in H we get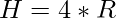
Hence, applying the formula of volume of cone and putting 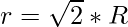 and
and 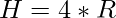 we get the desired result.
we get the desired result.
C++
#include<bits/stdc++.h>
using namespace std;
float Volume_of_cone(float R)
{
float V = (1 / 3.0) * (3.14) * (2 * ( R * R ) ) * (4 * R);
return V;
}
int main()
{
float R = 10.0;
cout << Volume_of_cone(R);
}
|
Java
import java.util.*;
class GFG{
static double Volume_of_cone(double R)
{
double V = (double)((1 / 3.0) * (3.14) * (2 * (R * R)) *
(4 * R));
return V;
}
public static void main(String[] args)
{
double R = 10.0;
System.out.print(Volume_of_cone(R));
}
}
|
Python3
import math
def Volume_of_cone(R):
V = (1 / 3) * (3.14) * (2 * ( R**2 ) ) * (4 * R)
return V
if __name__ == "__main__":
R = 10
print(Volume_of_cone(R))
|
C#
using System;
class GFG{
static double Volume_of_cone(double R)
{
double V = (double)((1 / 3.0) * (3.14) *
(2 * (R * R)) * (4 * R));
return V;
}
public static void Main()
{
double R = 10.0;
Console.Write(Volume_of_cone(R));
}
}
|
Javascript
<script>
function Volume_of_cone( R)
{
let V = ((1 / 3.0) * (3.14) * (2 * (R * R)) * (4 * R));
return V;
}
let R = 10.0;
document.write(Volume_of_cone(R));
</script>
|
Output: 8373.333333333332
Time complexity: O(1) since performing constant operations
Auxiliary space: O(1) since using constant variables
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...