Linear programming is a mathematical concept that is used to find the optimal solution of the linear function. This method uses simple assumptions for optimizing the given function. Linear Programming has a huge real-world application and it is used to solve various types of problems.
Linear programming is used in various industries such as shipping industries, manufacturing industries, transportation industries, telecommunications, and others.
Term “linear programming” consists of two words linear and programming, the word linear tells the relation between various types of variables of degree one used in a problem and the word programming tells us the step-by-step procedure to solve these problems.
In this article, we will learn about linear programming, its examples, formulas, and other concepts in detail.
What is Linear Programming?
Linear programming or Linear optimization is a technique that helps us to find the optimum solution for a given problem, an optimum solution is a solution that is the best possible outcome of a given particular problem.
In simple terms, it is the method to find out how to do something in the best possible way. With limited resources, you need to do the optimum utilization of resources and achieve the best possible result in a particular objective such as least cost, highest margin, or least time.
The situation that requires a search for the best values of the variables subject to certain constraints is where we use linear programming problems. These situations cannot be handled by the usual calculus and numerical techniques.
Linear Programming Definition
Linear programming is the technique used for optimizing a particular scenario. Using linear programming provides us with the best possible outcome in a given situation. It uses all the available resources in a manner such that they produce the optimum result.
Components of Linear Programming
The basic components of a linear programming(LP) problem are:
- Decision Variables: Variables you want to determine to achieve the optimal solution.
- Objective Function: Mathematical equation that represents the goal you want to achieve
- Constraints: Limitations or restrictions that your decision variables must follow.
- Non-Negativity Restrictions: In some real-world scenarios, decision variables cannot be negative
Additional Characteristics of Linear Programming
- Finiteness: The number of decision variables and constraints in an LP problem are finite.
- Linearity: The objective function and all constraints must be linear functions of the decision variables. It means the degree of variables should be one.
Linear Programming Examples
We can understand the situations in which Linear programming is applied with the help of the example discussed below,
Suppose a delivery man has to deliver 8 packets in a day to the different locations of a city. He has to pick all the packets from A and has to deliver them to points P, Q, R, S, T, U, V, and W. The distance between them is indicated using the lines as shown in the image below. The shortest path followed by the delivery man is calculated using the concept of Linear Programming.
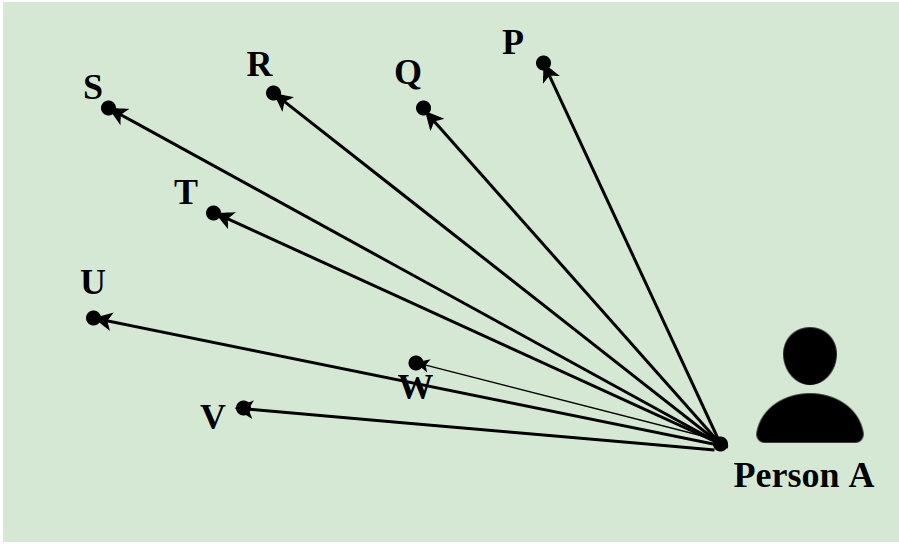
Linear Programming Problems
Linear Programming Problems (LPP) involve optimizing a linear function to find the optimal value solution for the function. The optimal value can be either the maximum value or the minimum value.
In LPP, the linear functions are called objective functions. An objective function can have multiple variables, which are subjected to conditions and have to satisfy the linear constraints.
Types of Linear Programming Problems
There are many different linear programming problems(LPP) but we will deal with three major linear programming problems in this article.
Manufacturing Problems
Manufacturing problems are a problem that deals with the number of units that should be produced or sold to maximize profits when each product requires fixed manpower, machine hours, and raw materials.
Diet Problems
It is used to calculate the number of different kinds of constituents to be included in the diet to get the minimum cost, subject to the availability of food and their prices.
Transportation Problems
It is used to determine the transportation schedule to find the cheapest way of transporting a product from plants /factories situated at different locations to different markets.
A linear programming problem consists of,
- Decision variables
- Objective function
- Constraints
- Non-Negative restrictions
Decision variables are the variables x, and y, which decide the output of the linear programming problem and represent the final solution.
The objective function, generally represented by Z, is the linear function that needs to be optimized according to the given condition to get the final solution.
The restrictions imposed on decision variables that limit their values are called constraints.
Now, the general formula of a linear programming problem is,
Objective Function: Z = ax + by
Constraints: cx + dy ≥ e, px + qy ≤ r
Non-Negative restrictions: x ≥ 0, y ≥ 0
In the above condition x, and y are the decision variables.
How to Solve Linear Programming Problems?
Before solving the linear programming problems first we have to formulate the problems according to the standard parameters. The steps for solving linear programming problems are,
Step 1: Mark the decision variables in the problem.
Step 2: Build the objective function of the problem and check if the function needs to be minimized or maximized.
Step 3: Write down all the constraints of the linear problems.
Step 4: Ensure non-negative restrictions of the decision variables.
Step 5: Now solve the linear programming problem using any method generally we use either the simplex or graphical method.
Linear Programming Methods
We use various methods for solving linear programming problems. The two most common methods used are,
- Simplex Method
- Graphical Method
Let’s learn about these two methods in detail in this article,
Linear Programming Simplex Method
One of the most common methods to solve the linear programming problem is the simplex method. In this method, we repeat a specific condition ‘n’ a number of times until an optimum solution is achieved.
The steps required to solve linear programming problems using the simplex method are,
Step 1: Formulate the linear programming problems based on the given constraints.
Step 2: Convert all the given inequalities to equations or equalities of the linear programming problems by adding the slack variable to each inequality where ever required.
Step 3: Construct the initial simplex table. By representing each constraint equation in a row and writing the objective function at the bottom row. The table so obtained is called the Simplex table.
Step 4: Identify the greatest negative entry in the bottom row the column of the element with the highest negative entry is called the pivot column
Step 5: Divide the entries of the right-most column with the entries of the respective pivot column, excluding the entries of the bottommost row. Now the row containing the least entry is called the pivot row. The pivot element is obtained by the intersection of the pivot row and the pivot column.
Step 6: Using matrix operation and with the help of the pivot element make all the entries in the pivot column to be zero.
Step 7: Check for the non-negative entries in the bottommost row if there are no negative entries in the bottom row, end the process else start the process again from step 4.
Step 8: The final simplex table so obtained gives the solution to our problem.
Linear Programming Graphical Method
Graphical Method is another method than the Simplex method which is used to solve linear programming problems. As the name suggests this method uses graphs to solve the given linear programming problems. This is the best method to solve linear programming problems and requires less effort than the simplex method.
While using this method we plot all the inequalities that are subjected to constraints in the given linear programming problems. As soon as all the inequalities of the given LPP are plotted in the XY graph the common region of all the inequalities gives the optimum solution. All the corner points of the feasible region are calculated and the value of the objective function at all those points is calculated then comparing these values we get the optimum solution of the LPP.
Example: Find the maximal and minimal value of z = 6x + 9y when the constraint conditions are,
- 2x + 3y ≤ 12
- x and y ≥ 0
- x + y ≤ 5
Solution:
Step 1: First convert the inequations into normal equations. Hence the equations will be 2x+3y = 0, x = 0, y = 0 and x + y = 5.
Step 2: Find the points at which 2x + 3y and x + y = 5 cut the x-axis and y-axis. To find the point of intersection of the x-axis put y = 0 in the respective equation and find the point. Similarly for y-axis intersection points put x = 0 in the respective equation.
Step 3: Draw the two lines cutting the x-axis and y-axis. We find that the two axes cut each other at (3,2).
Step 4: For x ≥ 0 and y ≥ 0, we find that both inequations are followed. Hence the region will include an area region enclosed by two axes and both lines including the origin. The plotted region is shown below in the figure.
Step 5: Find Z for each point and maxima and minima.
| Coordinates |
Z = 6x + 9y |
| (0,5) |
Z = 45 |
| (0,4) |
Z = 36 |
| (5,0) |
Z = 30 |
| (6,0) |
Z = 36 |
| (3,2) |
Z = 36 |
Hence, we find that Z = 6x + 9y is maximum at (0,5) and minimum at (5,0).

Linear Programming Applications
Linear Programming has applications in various fields. It is used to find the minimum cost of a process when all the constraints of the problems are given. It is used to optimize the transportation cost of the vehicle, etc. Various applications of Linear Programming are
Engineering Industries
Engineering Industries use linear programming to solve design and manufacturing problems and to get the maximum output from a given condition.
Manufacturing Industries
Manufacturing Industries use linear programming to maximize the profit of the companies and to reduce the manufacturing cost.
Energy Industries
Energy companies use linear programming to optimize their production output.
Transportation Industries
Linear programming is also used in transportation industries to find the path to minimize the cost of transportation.
Importance of Linear Programming
Linear Programming has huge importance in various industries it maximizes the output value while minimizing the input values according to various constraints.
LP is highly applicable when we have multiple conditions while solving a problem and we have to optimize the output of the problem i.e. either we have to find the minimum or the maximum value according to a given condition.
Read More,
Linear Programming Problems
Problem 1: A company manufactures and sells two types of products and the cost of production of each unit a and b is rupees 200 and 150 respectively each unit of product yields a profit of 20 rupees and each unit of product b yields a profit of 15 rupees on selling. The company estimates the monthly demand of A and B to be at a maximum of the harvested unit in all the production budget for the month is set at rupees 50000. How many units should the company manufacture to earn maximum profit from its monthly sales from a and b?
Solution:
Let x = number of units of type A
y = Number of units of type B
Maximize Z = 40x + 50y
Subject to the constraints
3x + y ≤ 9
x + 2y ≤ 8
and x, y ≥ 0
Consider the equation,
3x + y = 9
x = 3
y = 0
and x + 2y = 8
x = 8
y = 0
Now, we can determine the maximum value of Z by evaluating the value of Z at the four points (vertices) is shown below
|
Vertices
|
Z = 40x + 50y
|
|
(0, 0)
|
Z = 40 × 0 + 50 × 0 = Rs. 0
|
|
(3, 0)
|
Z = 40 × 3 + 50 × 0 = Rs. 120
|
|
(0, 4)
|
Z = 40 × 0 + 50 × 4 = Rs. 200
|
|
(2, 3)
|
Z = 40 × 2 + 50 × 3 = Rs. 230
|
Maximum profit, Z = Rs. 230
∴ Number of units of type A is 2 and the number of units of type B is 3.
Problem 2: Maximize Z = 3x + 4y.
Subject to constraints , x + y ≤ 450, 2x + y ≤ 600 and x, y ≤ 0.
Solution:
We have from the given
Constraints (1)
X + Y = 450
Putting x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Putting y = 0, ⇒ x + 0 = 450 ⇒ x = 450
From, Constraints (2)
2x + y = 600
Putting x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Putting y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Now, we have the points co-ordinate Z = 3x + 4y
|
Vertices
|
Z = 3x + 4y
|
|
(0, 0)
|
Z = 3 × 0 + 4 × 0 = 0
|
|
(300, 0)
|
Z = 3 × 300+ 4 × 0 = 900
|
|
(150, 300)
|
Z = 3 × 150 + 4 × 300 = 1650
|
|
(0, 450)
|
Z = 3 × 0 + 4 × 450 = 1800
|
Therefore, the optimal solution maximum Z = 1800 at co-ordinate x = 0 and y = 450. The graph is given below.
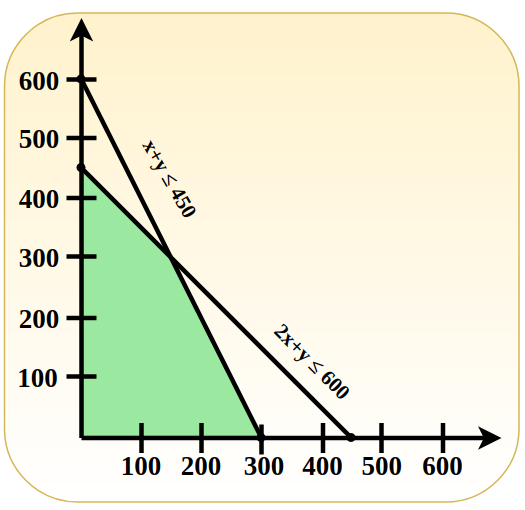
Up-to-Date Applications of Linear Programming
Linear programming, a powerful mathematical technique, is used to solve optimization problems in various industries. Here are some modern applications:
- Supply Chain Optimization: Linear programming helps companies minimize costs and maximize efficiency in their supply chains. It’s used for determining the most cost-effective transportation routes, warehouse operations, and inventory management strategies.
- Energy Management: In the energy sector, linear programming is utilized to optimize the mix of energy production methods. This includes balancing traditional energy sources with renewable ones to reduce costs and environmental impact while meeting demand.
- Telecommunications Network Design: Linear programming aids in designing efficient telecommunications networks. It helps in allocating bandwidth, designing network layouts, and optimizing the flow of data to ensure high-speed communication at lower costs.
- Financial Planning: Businesses and financial analysts use linear programming for portfolio optimization, risk management, and capital budgeting. It helps in making investment decisions that maximize returns while minimizing risk.
- Healthcare Logistics: In healthcare, linear programming is applied to optimize the allocation of resources, such as hospital beds, medical staff, and equipment. It’s crucial for improving patient care, reducing wait times, and managing costs effectively.
- Manufacturing Process Optimization: Linear programming is used to determine the optimal production levels for multiple products within a manufacturing facility, considering constraints like labor, materials, and machine availability.
- Agricultural Planning: Farmers and agricultural planners use linear programming to decide on crop selection, land use, and resource allocation to maximize yields and profits while conserving resources.
- Airline Crew Scheduling: Airlines employ linear programming to schedule crews efficiently, ensuring that flights are staffed in compliance with regulations and minimizing operational costs.
These applications demonstrate the versatility and power of linear programming in solving complex optimization problems across various sectors, showcasing its relevance in today’s data-driven world.
Linear Programming in Operations Research
- Core Tool: Linear programming is a foundational tool in operations research for optimizing resources.
- Decision Making: Helps in making the best decisions regarding resource allocation, maximizing profits, or minimizing costs.
- Wide Applications: Used in various fields such as logistics, manufacturing, finance, and healthcare for solving complex problems.
- Modeling Real-World Problems: Transforms real-world problems into mathematical models to find the most efficient solutions.
Simplex Method
- Optimization Algorithm: The Simplex Method is a powerful algorithm used in linear programming to find the optimal solution to linear inequalities.
- Step-by-Step Approach: It iteratively moves towards the best solution by navigating the edges of the feasible region defined by constraints.
- Efficiency: Known for its efficiency in solving large-scale linear programming problems.
- Versatility: Applicable in various domains like diet planning, network flows, production scheduling, and more, showcasing its versatility.
Linear Programming – FAQs
What is Linear Programming?
Linear programming is a mathematical concept which is used to optimize a given linear problem which has a variety of constraints. Using linear programming we the optimum output of the given problem
What are Linear Programming Problems?
Linear Programming Problems (LPP) are the problems which give the optimum solution to the given conditions.
What is Linear Programming Formula?
General Linear Programming Formulas are,
- Objective Function: Z = ax + by
- Constraints: px + qy ≤ r, sx + ty ≤ u
- Non-Negative Restrictions: x ≥ 0, y ≥ 0
What are the different types of Linear Programming?
Different types of linear programming methods are,
- Linear Programming by Simplex Method
- Linear Programming by R Method
- Linear Programming by Graphical Method
What are requirements of Linear Programming?
Various requirements of linear programming problems are,
- Linearity
- Objective Function
- Constraints
- Non-negativity
What are the advantages of Linear Programming?
Various advantages of linear programming are,
- It provides the optimal solution to any given linear problem.
- It is easy to use and always gives consistent results
- It helps to maximize profits and to reduce the input cost.
Share your thoughts in the comments
Please Login to comment...