Group Isomorphisms and Automorphisms
Last Updated :
04 Nov, 2022
Prerequisite – Group
Isomorphism :
For two groups (G,+) and (G’,*) a mapping f : G → G’ is called isomorphism if
- f is one-one
- f is onto
- f is homomorphism i.e. f(a + b) = f(a) * f(b) ∀ a, b ∈ G.
In brief, a bijective homomorphism is an isomorphism.
Isomorphic group :
If there exists an isomorphism from group (G,+) to (G’,*). Then a group (G,+) is called isomorphic to a group (G’,*)
It is written as G ≅ G’ .
Examples –
1. f(x)=log(x) for groups (R+,*) and (R,+) is a group isomorphism.
Explanation –
- f(x)=f(y) => log(x)=log(y) => x=y , so f is one-one.
- f(R+)=R , so f is onto.
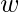
- f(x*y)=log(x*y)=log(x)+log(y)=f(x)+f(y) , so f is a homomorphism.
2. f(x)=ax for group (Z,+) to (aZ,+) , where a is any non zero no.
Explanation –
- f(x)=f(y) => ax=ay => x=y , so f is one-one.
- f(Z)=aZ , so f is onto.
- f(x + y) =ax + ay= f(x) + f(y), so f is a homomorphism.
3. The function f from group of cube roots of unity {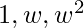 } with a multiplication operation is an isomorphism to group residual classes mod(3) {{0},{1},{2}} with the operation of addition of residual classes mod(3) such that f(1)={0}, f(
} with a multiplication operation is an isomorphism to group residual classes mod(3) {{0},{1},{2}} with the operation of addition of residual classes mod(3) such that f(1)={0}, f(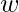 )={1} and f(
)={1} and f(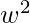 )={2}.
)={2}.
Explanation –
- Clearly, f is onto and one-one.
- Also f(1*
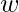 ) = f(
) = f(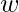 ) = {1} = {0} +3 {1} = f(1)*f(
) = {1} = {0} +3 {1} = f(1)*f(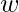 ).
).
f(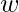 *
*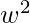 ) = f(1) = {0} = {1} +3 {2} = f(
) = f(1) = {0} = {1} +3 {2} = f(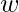 )*f(
)*f(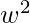 ).
).
and f(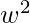 *1) = f(
*1) = f(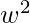 ) = {2}={2} +3 {0} = f(
) = {2}={2} +3 {0} = f(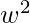 )*f(1). So f is homomorphism.
)*f(1). So f is homomorphism.
All this proves that f is an isomorphism for two referred groups.
4. f(x)=ex for groups (R,+) and (R+,*) where R+ is a group of positive real numbers and x is an integer.
5.Groups ({0,1,2,3},+4) and ({2,3,4,1},+5) are isomorphic.
NOTE :
- If there is a Homomorphism f form groups (G,*) to (H,+) . Then f is also a Isomorphism if and only if Ker(f)={e} .Here e is the identity of (G,*).
Also, Ker(f) = Kernel of a homeomorphism f :(G,*) → (H,+) is a set of all the elements in G such that an image of all these elements in H is the identity element e’ of (H,+) . - If two groups are isomorphic, then both will be abelians or both will not be. Remember a group is Abelian if it is commutative.
- A set of isomorphic group form an equivalence class and they have identical structure and said to be abstractly identical.
Automorphism :
For a group (G,+), a mapping f : G → G is called automorphism if
- f is one-one.
- f homomorphic i.e. f(a +b) = f(a) + f(b) ∀ a, b ∈ G.
Examples –
1. For any group (G,+) an identity mapping Ig: G → G, such that Ig(g)=g , ∀g ∈ G is an automorphism.
Explanation-
- as if I(a)=I(b) => a=b so I is one-one.
- as I(a+b) =a+b =I(a)+I(b), so I is also a homomorphism.
2. f(x)=-x for group (Z,+).
Explanation-
- as if f(a)=f(b) => -a=-b => a=b so f is one-one.
- as if f(a+b) =-(a+b) =(-a)+(-b) =f(a)+f(b), so f is also a homomorphism.
3. f(x)=axa-1 for a group (G,+) ∀a ∈ G.
Explanation –
- as f(n)=f(m) => ana-1 = ama-1 => n = m so f is one-one.
- as f(n+m)= a(n+m)a-1 =ana-1 + ama-1 = f(n) + f(m), so f is also homomorphism.
4. f(z)= for groups of complex numbers with addition operation.
for groups of complex numbers with addition operation.
Remember f is complex conjugate such that if z=a+ib then f(z)= =
=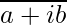 =a-ib.
=a-ib.
5.f(x)=1/x is automorphism for a group (G,*) if it is Abelian.
NOTE :
- A set of all the automorphisms( functions ) of a group, with a composite of functions as binary operations forms a group.
- Simply, an isomorphism is also called automorphism if both domain and range are equal.
- If f is an automorphism of group (G,+), then (G,+) is an Abelian group.
- Identity mapping as we see, in example, is an automorphism over a group is called trivial automorphism and other non-trivial.
- Automorphism can be divided into inner and outer automorphism.
Share your thoughts in the comments
Please Login to comment...