Geometry and Co-ordinates

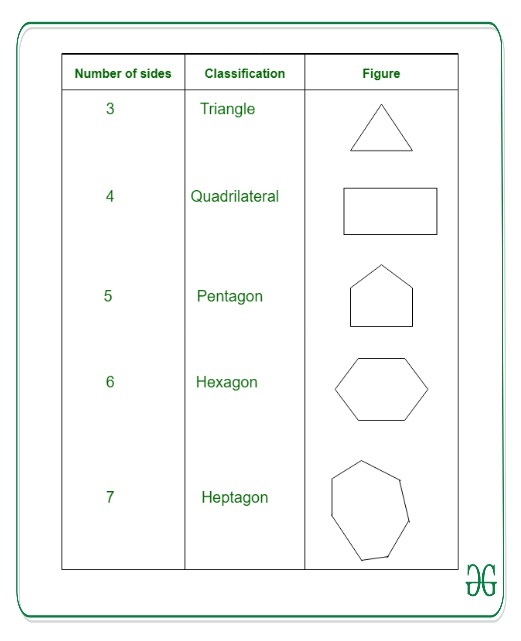
Polygons

Polygons are planes figures formed by a closed series of rectilinear segments. Ex– Triangle, Rectangle etc. 

Properties: 
1. Sum of all the angles of a polygon with n sides = (n-2)π 
2. Sum of all exterior angles = 360° 
3. No. of sides = 360°/exterior angle 

Classification of polygons –

Triangles

A triangle is a polygon having three sides. 
Area: 
1. Area = 1/2 x base x height 
2. Area = √s(s-a)(s-b)(s-c) where s = a+b+c/2 
3. Area = rs (where r is in-radius) 
4. Area = 1/2 x product of two sides x sine of angle 
5. Area = abc/4R where R = circumradius 

Congruency of Triangles:
1. SAS congruency: If two sides and an included angle of one triangle are equal to two sides and an included angle of another, the two triangles are congruent. 
2. ASA congruency: If two angles and the included side of one triangle is equal to two angles and the included side of another, the triangles are congruent. 
3. AAS congruency: If two angles and side opposite to one of the angles is equal to the corresponding angles and sides of another triangle, the triangles are congruent. 
4. SSS congruency: If three sides of one triangle are equal to three sides of another triangle, the two triangles are congruent. 
5. SSA congruency: If two sides and the angle opposite the greater side of one triangle are equal to the two sides and the angle opposite to the greater side of another triangle, then triangle are congruent. 

Similarity of Triangles:
1. AAA similarity: If in two triangles, corresponding angles are equal, then the triangles are similar. 
2. SSS similarity: If the corresponding sides of two triangles are proportional then they are similar. 
3. SAS similarity: If in two triangles, one pair of corresponding sides are proportional and the included angles are equal then the two triangles are similar. 

Equilateral triangles:

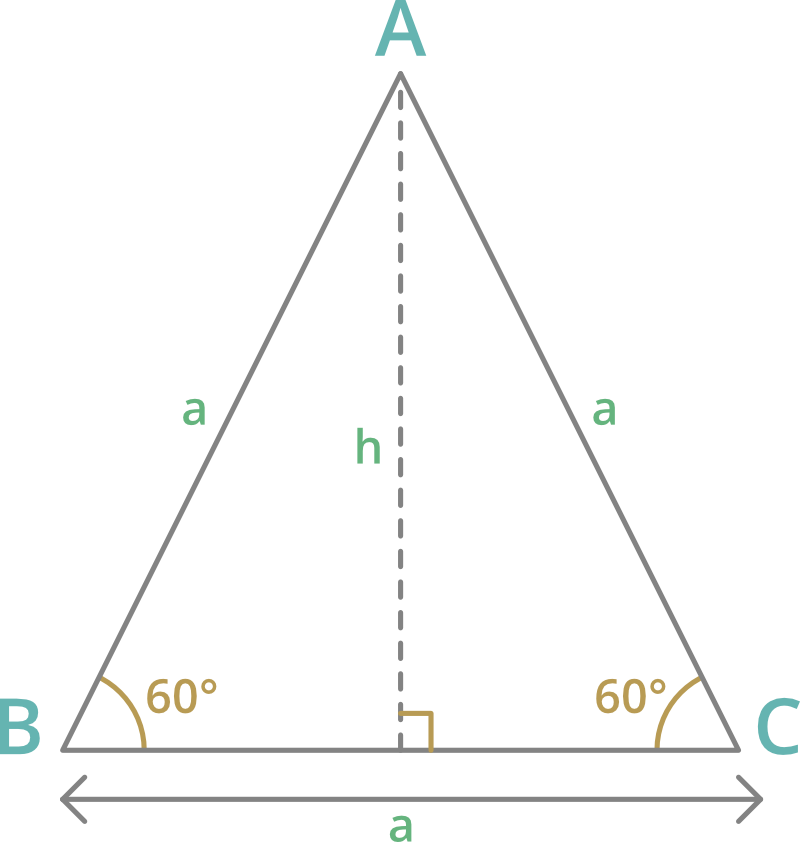
1. Height = a√3/2 
2. Area = √3a²/4 
3. R(circum radius) = 2h/3 = a/√3 
4. r(in radius) = h/3 = a/2√3 
5. In equilateral triangle orthocenter, in-centre, circumcenter and centroid coincide. 

Isosceles triangle:

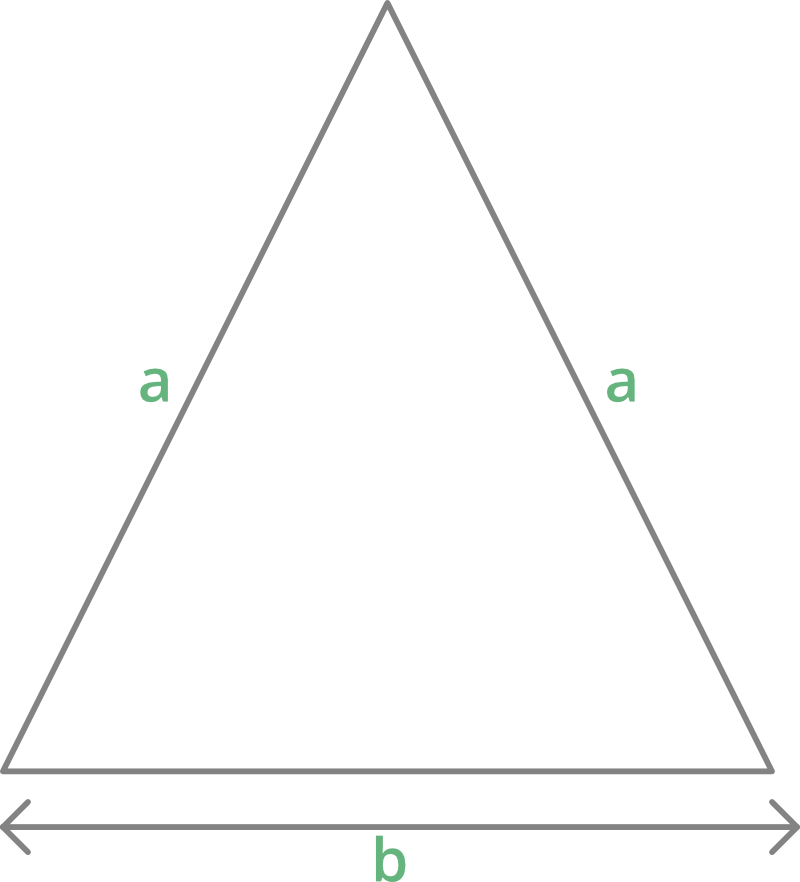
Area = b/4√(4a² – b²) 
where b=base and a=equal sides 

Important terms:
1. Median: A line joining the mid-point of a side of a triangle to the opposite vertex is called a radian. 

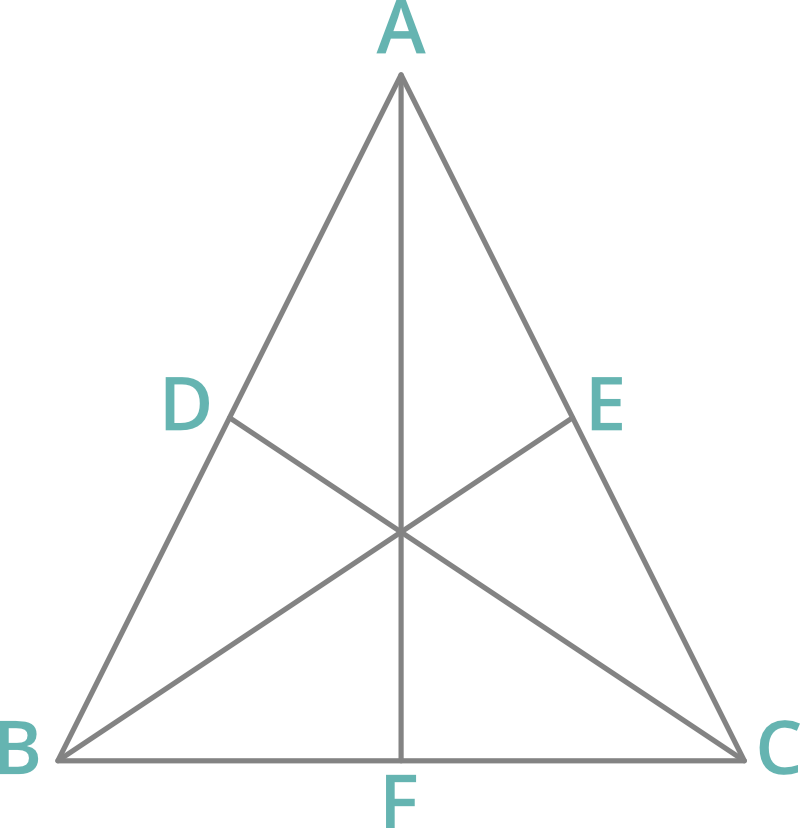
• A median divides a triangle in two parts of equal area. 
  
• The point where three medians meet is called centroid of the triangle. 
  
• The centroid of a triangle divides each median in ratio 2:1. 
  

2. Altitude: A perpendicular drawn from any vertex to the opposite side is called the altitude. 

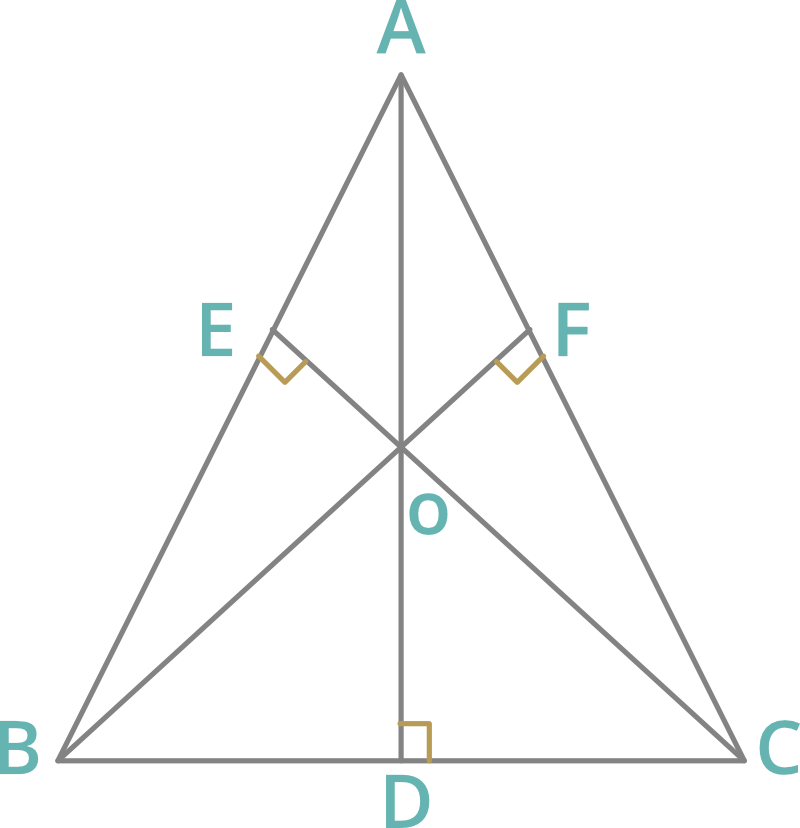
• The point where all altitudes meet at a point is called the orthocenter of triangle. 
  

3. Perpendicular bisector: A line that is a perpendicular to a side and bisects it is the perpendicular bisector of the side. 

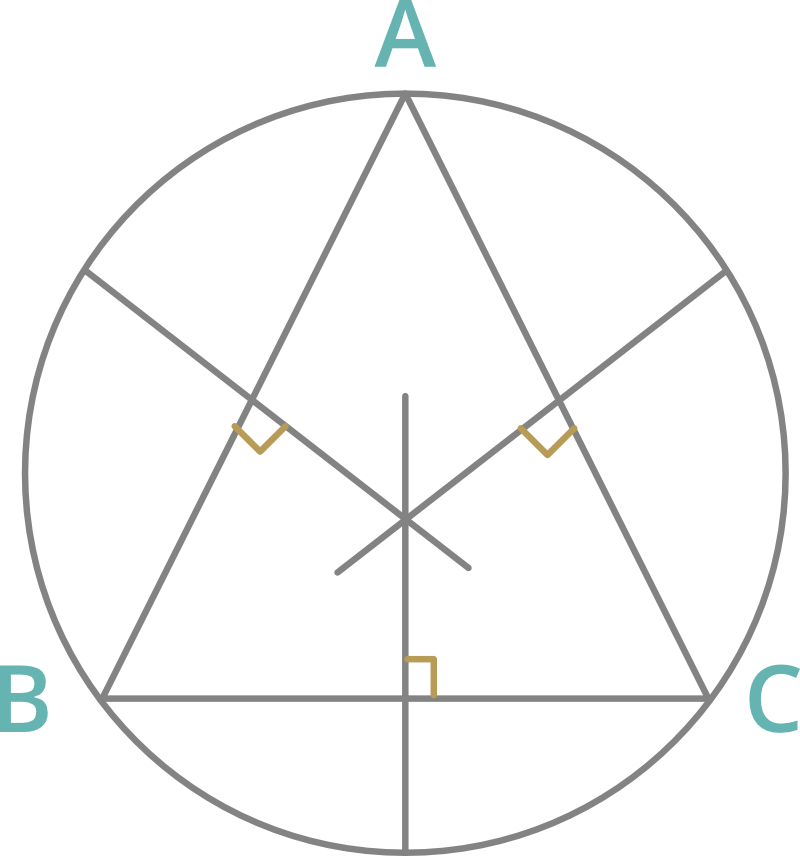
• The point at which perpendicular bisectors of the sides meet is called the circumcenter. 
  
• The circumcenter is the centre of the circle that circumscribes the triangle. 
  

4. Incentre:

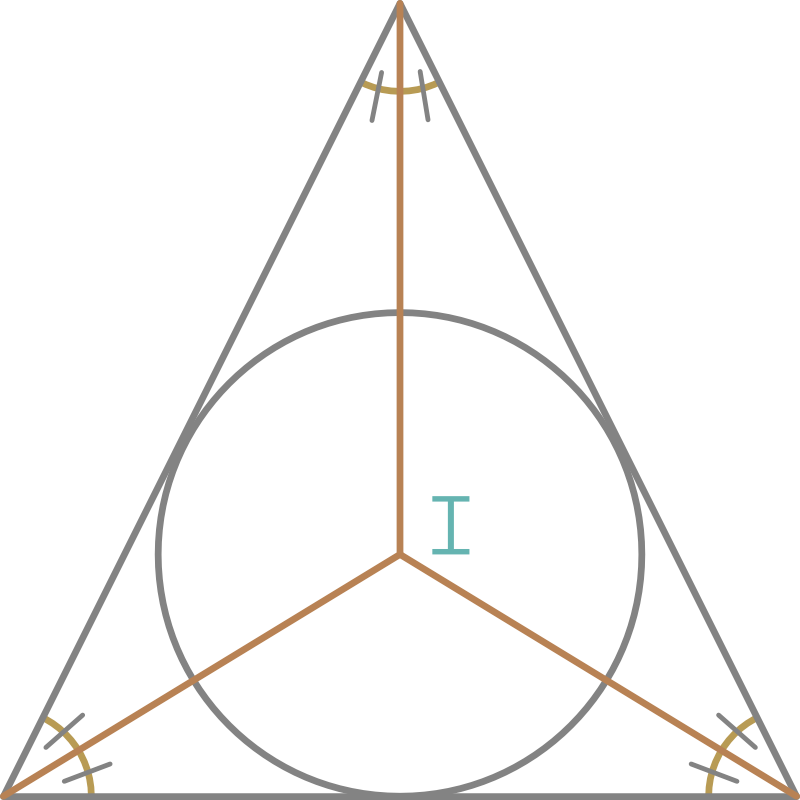
• The lines bisecting the interior angles of a triangle are the angle bisectors of that triangle. 
  
• The angle bisectors meet at a point called the incentre. 
  
• The angle formed by any side at the incentre is always 90° more than the half of angle opposite to the side. 
  

Tangents:

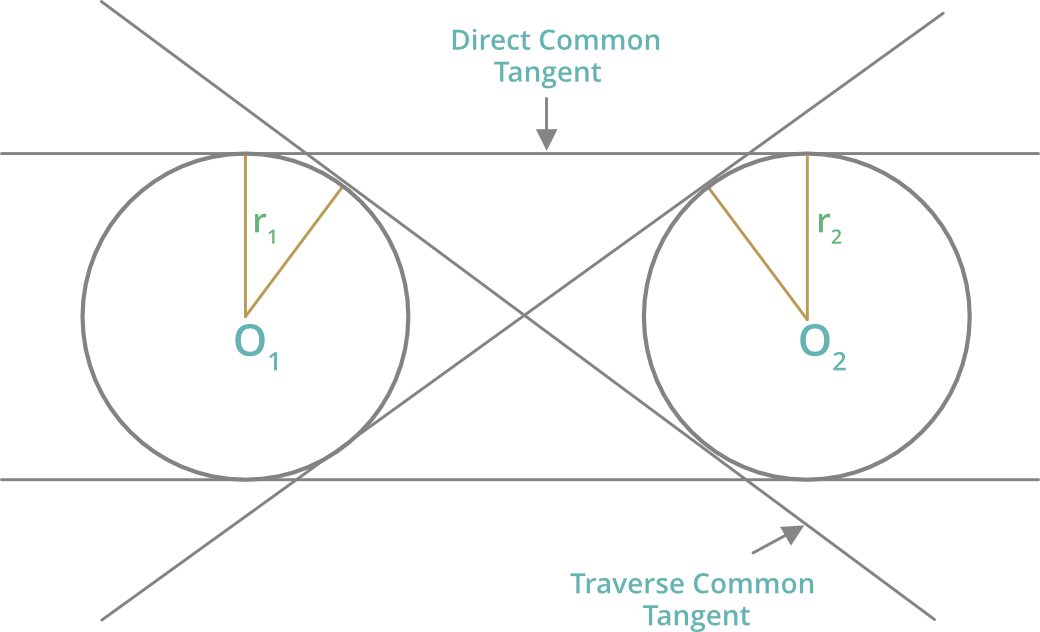
1. Length of direct common tangents is 
= √[(Distance between their centres)²-(r₁ – r₂)²] 
= √[(O₁O₂)² – (r₁ – r₂)²] 

2. Length of traverse common tangents is 
= √[(Distance between their centres)²-(r₁ + r₂)²] 
= √[(O₁O₂)² – (r₁ + r₂)²] 

Sample Problems

Question 1: If each interior angle of a regular polygon is 108°. The number of sides of the polygon is 
Solution : Interior angle = 108° 
Exterior angle = 180 – 108 = 72 
Number of sides of polygon = 360° /exterior angle 
= 360° /72 
= 5 

Questions 2: The ratio of angles of triangle is 2:3:5. Find the smallest angle of the triangle. 
Solution : Ratio of angles 2:3:5 
then 2x + 3x + 5x = 180 
10x = 180 
x = 18 
Hence, the smallest angle = 18×2 = 36° 

Question 3: Two medians AD and BE of ∆ABC intersect O at right angle. If AD = 9cm and BE = 6cm, then the length of BD is 
Solution :

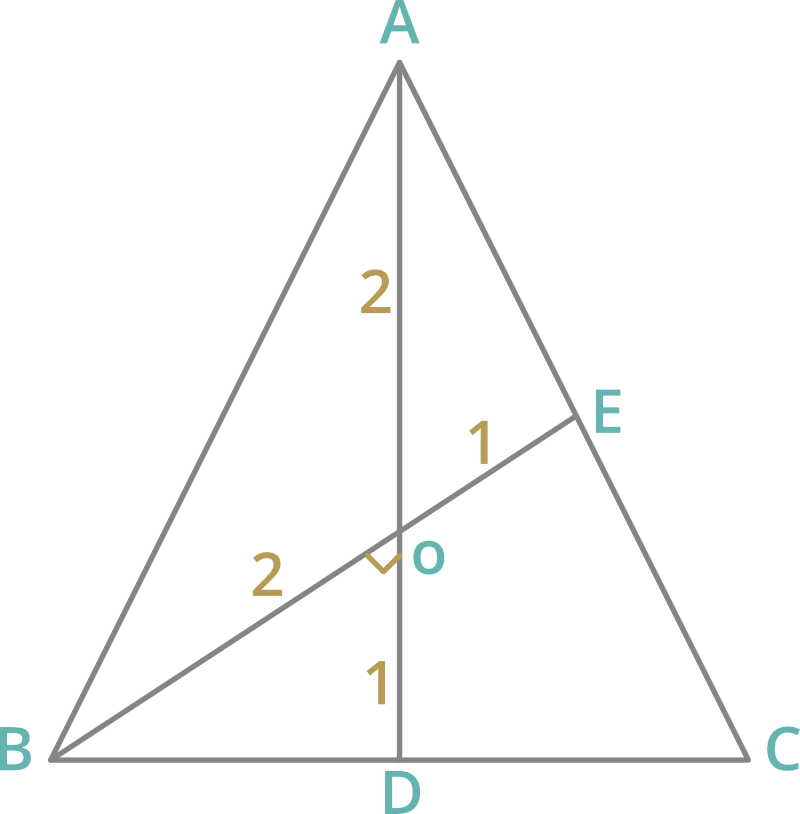
O is the centroid which divides the median in 2:1. 
So, AO:OD = 2:1 
AD = 3 units -> 9 cm 
1 unit -> 3 cm 
So, OD = 3 cm 
BE = 3 units -> 6cm 
So, BO = 4 cm 
∆BOD is a right angled triangle. 
BD² = BO² + OD²
BD² = (4)² + (3)²
BD² = 16 + 9 = 25 
BD = 5 cm 

Question 4: The side AB of a parallelogram ABCD is produced to E in such a way that BE = AB, DE intersects BC at Q. The point Q divides BC in the ratio 
Solution : Acc. to question 

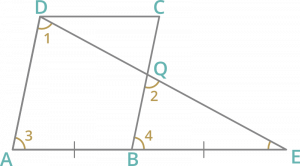
AD || BC and AB || DC 
∠1 = ∠2 (Corresponding alternate angle) 
∠3 = ∠4 (Corresponding alternate angle) 
and ∠BEQ is common 
By AAA property both are similar ∆EQB ∼ ∆EDA 
So, EB/EA = EQ/ED = QB/AD 
AD=BC & EA = 2EB 
then 1/2 = QB/BC 
=> BQ = QC 
Hence, Q divides BC in ratio 1:1. 

Question 5: In a ∆ABC, AB=AC and BA is produced to D such that AC=AD. Then the ∠BCD is 
Solution :Acc. to question 

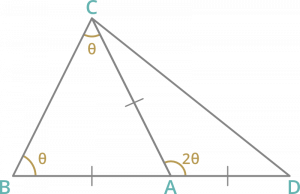
ABC is an isosceles triangle. 
=> ∠C = ∠B = θ 
=> ∠CAD = ∠C + ∠B = 2θ (An exterior angle of a triangle is equal to the sum of the opposite interior angles.) 
AC=AD So, ∆ADC is also an isosceles triangle. 
In ∆ADC, ∠A + ∠C + ∠D = 180° 
2∠C = 180° – 2θ (∠C = ∠D) 
∠C = 90° – θ 
∠BCD = θ + 90° – θ 
∠BCD = 90° 

Question 6: If O is the circumcenter of ∆PQR, and ∠QOR = 110°, ∠OPR= 25°, then the angle ∠PRQ is 
Solution :

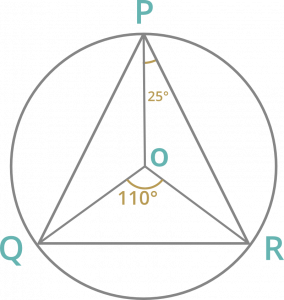
If O is the circumcenter then OP=OR=OQ. 
∠OPR = 25° 
then ∠PRO = 25° 
In ∆OQR 
∠OQR + ∠ORQ + ∠QOR = 180° 
2∠ORQ = 180° – 110° 
∠ORQ = 35° 
So, ∠PRQ = ∠PRO + ∠ORQ 
= 25° + 35° 
= 60° 

Question 7: In ∆ABC, DE || AC, D and E are two points on AB and CB respectively. If AB=20 cm and AD = 8 cm, then BE : CE is 
Solution :

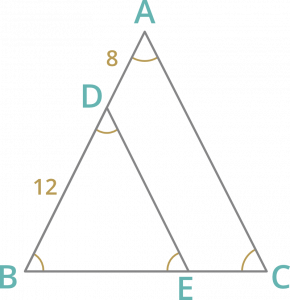
AB = 20 cm and AD = 8 cm 
DE || AC 
then, ∠A = ∠D and ∠C = ∠E 
∠B is common 
By AAA property, ∆ABC ∼ ∆DBE 
therefore BD/AD = BE/CE 
BE/CE = 12/8 
BE/CE = 3/2 
Hence, BE : CE = 3:2 

Question 8: Angle between the internal bisectors of two angles of a triangle ∠B and ∠C is 110°, then ∠A is 
Solution :

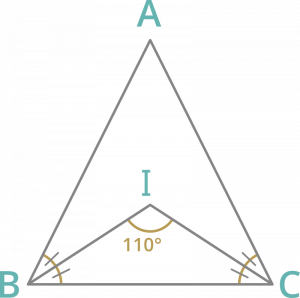
Internal bisectors of angles intersect each other at Incentre. 
∠BIC = 110° 
The angle formed by any side at the incentre is always 90° more than the half of angle opposite to the side.So, 
∠BIC = 90° + 1/2∠A 
1/2∠A = 110° – 90° 
∠A = 20×2 = 40° 

Question 9: The distance between two parallel chords of length 8 cm and each in a circle of diameter 10cm is 
Solution :

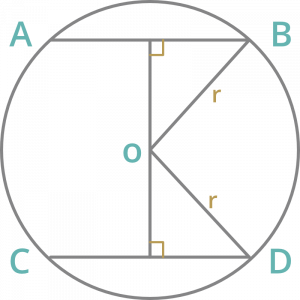
AB = CD = 8 cm 
radius = D/2 = 10/2 = 5 cm 
In ∆OMB 
OB²=OM² + MB²
5² = OM² + 4²
OM² = 25 – 16 
OM = 3 cm 
MN = 2 x OM = 2 x 3 = 6 cm 

Question 10: The radius of two concentric circles are 12cm and 13cm. If the chord of the greater circle be a tangent to the smaller circle, then the length of that chord is: 
Solution : Acc. to Question 

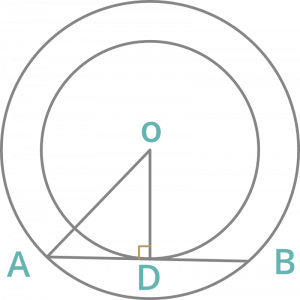
AO = 13 cm and OD = 12 cm 
In ∆AOD 
AO²= DO² + AD²
13² = 12² + AD²
AD² = 169 – 144 
AD = 5cm 
AB = 2xAD = 10 cm 

Questions 11: Two tangents are drawn at the extremities of diameter AB of a circle with centre O. If a tangent to the circle at the point C intersects the other two tangents at Q and R, then the measure of the ∠QOR is 
Solution : Acc. to question 

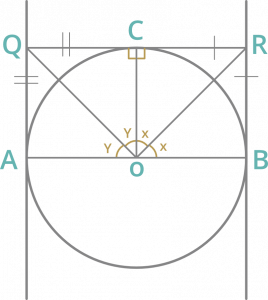
In ∆OCR and ∆RBO 
OC = OB (radius) 
RC = RB (tangent from same point) 
PR is common 
By SSS property both are congruent ∆OCR ≅ ∆RBO 
Similarly they are also congruent ∆OCQ ≅ ∆QAO 
Then ∠COR = ∠ROB = x 
and ∠AOQ = ∠COQ = y 
2x + 2y = 180° 
x + y = 90° 
∠QOR = 90° 

Question 12: Two equal circles whose centres are O and O’ intersect each other at the point A and B, OO’= 24 cm and AB = 10 cm then the radius of the circle is 
Solution :

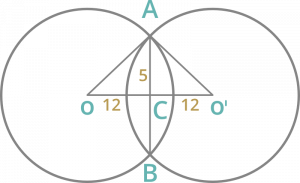
AB = 10 cm 
AC = BC = 5 cm 
OC = CO’ = 12 cm 
In right angled triangle ∆ACO 
OA² = OC² + AC²
OA² = 12² + 5²
OA² = 144 + 25 
OA = 13 cm 

Question 13: The distance between the centers of two circles of radii 6 cm and 3 cm is 15 cm. The length of the traverse common tangent to the circles is: 
Solution : Length of traverse common tangent = √[(Distance between their centres)²-(r₁ + r₂)²] 
=√[(15)²-(6 + 3)²] 
=√(225 – 81) 
= 12 cm 

Question 14: If the distance between two points (0, -5) and (x, 0) is 13 units, then the value of x is: 
Solution :We know that 
(Distance)² =[(x₂-x₁)² + (y₂ – y₁)²] 
(13)² = [(x₂-0)² + (0 – (-5) )²] 
169 = x² + 25 
x = 12 units