Rational Function

Rational Function is a type of function that is expressed as a fraction where both the numerator and denominator must be a polynomial and the denominator can never equal zero. Thus a rational function is similar to a fraction but the numerator and denominator are polynomial functions. In simple words, the rational function can be defined as the ratio of two polynomials. Rational functions find applications in various daily life problems and in various fields in life.

In this article, we shall discuss rational function in detail.

What are Rational Functions?

Rational Function which is also called rational expression, is a mathematical expression that represents the ratio of two polynomial functions and the denominator here can never be 0. For example, two polynomial expressions i.e., 2x – 7 and 3x²; can form two rational expressions. One of which is 2x-7/3x² and the other is 3x²/(2x-7). These functions are only defined when their denominator is non-zero.

Rational Function Definition

Mathematically, a rational function can be represented as f(x) = g(x)/h(x)

Where f(x), g(x) and h(x) are all polynomials in variable x and h(x)≠0.

For example f(x) = (x+1)/x is a rational function if x≠0.

Note: A function where the numerator is a polynomial but the denominator is a constant other than zero, is said to be a linear function and not a rational function.

Rational Functions Examples

Some examples of rational functions are as follows:

• x+1/(x+2)
• x²-1/(x²+1)
• 3x/(x²-4)
• x³/(x+8)
• 2x/(1-4x)
• 7x²/(8x³+4)

Properties of Rational Function

A rational function has various properties which are as follows:

• Domain of Rational Function
• Range of Rational Function
• Asymptotes of Rational Function
  • Horizontal Asymptote
  • Vertical Asymptote
  • Oblique Asymptote
• Holes of Rational Function

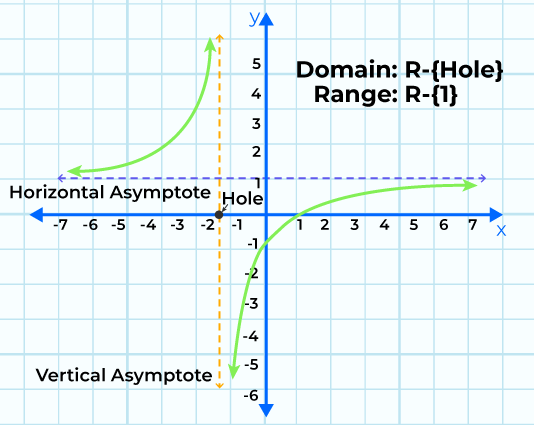
Domain of Rational Function

We know that the denominator is never zero in a rational function. This fact is used to find out the domain and range of the rational function. In order to calculate the domain of the rational function following steps are followed

• Keep the value of denominator equal to zero
• Find the values of variable where the denominator becomes zero.
• The domain of the function is thus the set of all real numbers R excluding the values which make the denominator zero.

Range of Rational Function

In order to calculate the range following steps are followed:

• Set f(x)=y
• Solve the equation so obtained for the variable x.
• Now use the condition of denominator nit equals to zero.
• Find the value of y from the above condition.
• The range of the function is set of all real number R excluding the value of y so obtained.

Let’s consider an example for understanding the domain and range of Rational Function.

Example: Consider a rational function (x+2)/(x+1), and find its domain and range.

Solution:

To calculate the domain of the given function, we can follow the following steps:

• Equate the denominator to zero i.e. x+1=0, which gives x=-1.
• Thus the domain of the function is R-{-1}.

The range of the function is calculated as follows:

• Set f(x)=y=(x+2)/(x+1)
• Solve the equation for x

y(x+1) = x+2

⇒ xy+y = x+2

⇒ xy-x = 2-y

⇒ x(y-1) = 2-y

⇒ x = 2-y/(y-1)

• Keep denominator not equals to zero i.e. y-1≠0 which gives y≠1.
• Thus range of the function is set of real numbers R-{1}.

Asymptotes of Rational Function

All the Rational Functions have three types of Asymptotes and they are,

• Vertical Asymptote
• Horizontal Asymptote
• Oblique Asymptote

Now, let’s learn about them in detail

Vertical Asymptote

A vertical asymptote of a rational function is a line parallel to the y-axis and is of the form x=a where a is any number. This line appears to touch the graph of the rational function but it never touches it actually. There can be one or more vertical asymptote of a rational function. In order to find the vertical asymptote of the rational function, following steps are followed:

• Reduce the rational function to its lowest form and eliminate all the common terms in numerator and denominator.
• Set the denominator equal to zero and find the value of the variable for which denominator becomes zero.

Horizontal Asymptote

A horizontal asymptote of a rational function is a line parallel to the x-axis and is of the form y=a where a is any number. This line appears to touch the graph of the rational function but it never touches it actually. There can be only one horizontal asymptote of a rational function. Horizontal asymptote of a rational function can be calculated by comparing the degrees of numerator and denominator as follows:

• Let N and D be the degree of numerator and denominator respectively.
• If N < D, horizontal asymptote is y=0
• If N > D, then there is no horizontal asymptote
• If N = D, y = ratio of leading coefficients in numerator and denominator is the horizontal asymptote.

Oblique Asymptote

It is a slant line which appears to touch the graph of the rational function but never touches it. It is present only in the case where degree of numerator N = degree of denominator D+1. The horizontal asymptote is equal to the quotient which is the result of division of numerator and denominator of the rational function.

Holes of Rational Function

The points that appear to be present on the graph of the rational function but are actually not present are called holes of rational function. In order to calculate the holes, first reduce the function to lowest form and set the common factor equal to zero. The value of the variable and value of function at that variable is the required hole.

Simplifying Rational Functions

In order to simplify the rational function, we need to reduce it to its lowest form. The steps to be followed are:

• Step 1: Factorise the numerator and denominator.
• Step 2: Cancel out the common terms from both numerator and denominator. The function thus obtained is the simplified form of the given rational function.

For example: Consider the function (x²+2x+1)/(x²+3x+2). In order to simplify the given function we proceed as follows:

• Factorise the numerator and denominator of the function

x²+x+x+1/(x²+x+2x+2)

x(x+1)+1(x+1)/[x(x+1)+2(x+1)

(x+1)(x+1)/(x+1)(x+2)

• As (x+1) is common in both numerator and denominator, we can cancel out (x+1)
• Thus the function is simplified and written as: x+1/(x+2)

Operations On Rational Functions

All the normal operations in mathematics can also be applied to rational functions. These basic operations are addition, subtraction, multiplication, and division. We will see how to perform these functions by considering two rational functions a/b and c/d.

Addition of Rational Functions

Addition of any two rational functions a/b and c/d is done as:

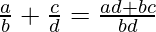
Subtraction of Rational Functions

Subtraction of any two rational functions a/b and c/d is done as:

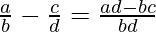
Multiplication of Rational Functions

Multiplication of any two rational functions a/b and c/d is done as:

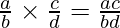
Division of Rational Functions

Division of any two rational functions a/b and c/d is done as:

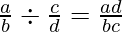
Graphing Rational Functions

In order to graph a rational function we need to follow the below steps:

• Find the vertical asymptote of the given rational function and mark it with a dotted line on the graph.
• Find the vertical asymptote of the given rational function and mark it with a dotted line on the graph.
• Find the holes of the rational function if they exist.
• Calculate the x and y intercept of the function by setting y and x equal to zero alternately.
• Draw a table containing two columns labelled x and y. Now write the x-intercepts and vertical asymptotes of the rational function in this table. Choose random numbers and write them in the column labelled x on either side of each of the x-intercepts and vertical asymptotes.
• Calculate the value of y or f(x) by substituting the chosen value of x in the rational function.
• Plot all the points obtained in the table and join them with a free hand as if drawing a curve without touching the asymptotes.

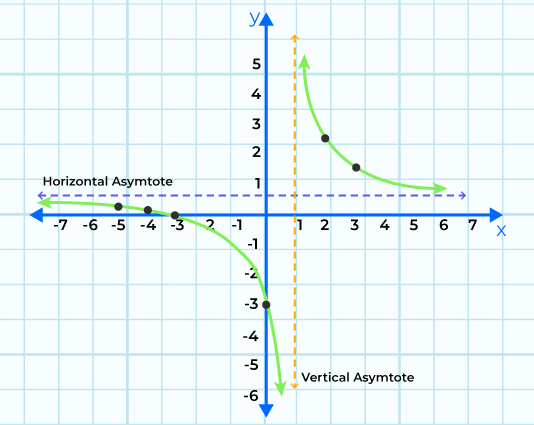
Example: Graph the function f(x) = (x + 3) / (x – 1).

Solution:

Given f(x) = (x + 3) / (x – 1) = y(let)

• Calculate the vertical asymptote by setting the denominator equal to zero:

x -1 = 0

x = 1

• Calculate horizontal asymptote. As degree of numerator and degree of denominator is same, horizontal asymptote is ratio of leading coefficients i.e. 1:1 which is y = 1.
• As there is no common factor between numerator and denominator, holes do not exist.
• Find x intercept by putting y = 0. Thus x intercept is:

(x + 3) / (x – 1) = 0

x = -3

So x intercept is (-3,0).

• Find y intercept by putting x = 0.

3/(-1) = y

y = -3

So y intercept is (0, -3).

• Draw a table containing two columns labelled x and y. Now write the x-intercepts and vertical asymptotes of the rational function in this table. Choose random numbers and write them in the column labelled x on either side of each of the x-intercepts and vertical asymptotes as follows:

x	y
-5	(-5+3)/(-5-1) = 1/3 = 0.3
-4	(-4 + 3) / (-4 – 1) = 1/5 = 0.2
-3	0 (x intercept)
-2	(-2 + 3) / (-2 – 1) = -1/3 =-0.33
0	-3 (y -intercept)
1	Vertical Asymptote
2	5
3	3

• Plot all these points on the graph as follows:

Read More,

• Domain and Range of a Function
• Relation and Function

Rational Functions Examples

Examples 1: Find the vertical asymptote of (x+1)/(2x+3).

Solution:

Given f(x) = (x+1)/(2x+3)

As the function is already in its lowest form and there is no common factor between numerator and denominator, vertical asymptote is calculated by simply equating the value of denominator equal to zero.

2x + 3 = 0

x = -3/2

Thus, x = -3/2 is the vertical asymptote of the given function.

Example 2: Find the horizontal asymptote of x³+x²+1/(2x+1).

Solution:

Given f(x) = x³+x²+1/(2x+1)

Degree of numerator N = 3

Degree of denominator D = 1

As N>D, there is no horizontal asymptote for given function.

Example 3: Find the oblique asymptote of (2x²+3)/(x+4).

Solution:

Given f(x) = 2x²+3/(x+4)

As degree of numerator = 2 = degree of denominator + 1, oblique asymptote is the quotient that is obtained by dividing numerator and denominator. The division is shown below:

As the quotient obtained is 2x, it is the oblique asymptote to the given function.

Example 4: Find the domain of the function x/(x²-1).

Solution:

Given f(x) = x/(x²-1)

• Equate the denominator to zero.

x² – 1 = 0

x = +1 or -1

Thus domain of the given function is set of real numbers excluding 1 and -1 which is R – {-1, 1}.

Example 5: Find the range of the function 4x+5/(6x+7).

Solution:

Given f(x) = 4x+5/(6x+7)

• Set f(x) = y

y = 4x+5/(6x+7)

• Solve for x

y(4x+5) = 6x+7

4xy+5y = 6x+7

4xy-6x = 7-5y

x(4y-6) = 7-5y

x = 7-5y/(4y-6)

• Keep denominator not equal to zero

4y – 6 ≠ 0

y ≠ 6/4

y ≠ 3/2

• Thus the range of function is set of real numbers excluding 3/2 which is R – {3/2}

Practise Problems on Rational Functions

Problem 1: Simplify the rational expression: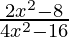 

Problem 2: Find the domain of the rational function: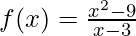 

Problem 3: Determine the vertical asymptotes, if any, for the rational function: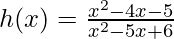 

Problem 4: Solve for x in the equation: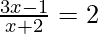 

Problem 5: Given the rational function 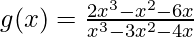, find the horizontal asymptotes, if they exist.

Rational Functions – FAQs

1. What do you Mean by Rational Function?

Rational function is a type of function which is expressed as a fraction where both numerator and denominator must be a polynomial and the denominator is never equal to zero.

2. How to Simplify a Rational Function?

A rational function is simplified by factorising the numerator and denominator and then cancelling out the common factors.

3. What are Conditions for a Function to be a Rational Function?

A rational function may have a constant numerator and a polynomial denominator or both numerator and denominator as polynomials. A rational function can never have constant denominator.

4. Why are functions called rational functions?

Functions are called rational functions when they are expressed as a ratio of two polynomials. The term “rational” comes from “ratio,” as these functions represent the ratio of two integers.

5. What is a rational and irrational function?

Rational functions are expressions where one polynomial is divided by another, resulting in a finite, well-defined output. Irrational functions involve radicals.

6. What is Meant by Domain and Range of a Function?

Domain of the function is the set of all the numbers for which the function produces a finite value. Range is the set of all values that are obtained when putting the variable in function equal to any value from the domain.

7. What are Asymptote?

Asymptotes are imaginary lines that a curve approaches but never quite touches. They describe behavior like the curve getting closer to a limit without reaching it.

8. How is Vertical Asymptote Calculated?

Vertical Asymptote is calculated by simplifying the rational function first and then setting the denominator equal to zero and finding the value of the variable for which denominator becomes zero.

9. What is meant by Horizontal Asymptote of Rational Function?

A horizontal asymptote of a rational function is a line parallel to the x-axis and is of the form y=a where a is any number. This line appears to touch the graph of the rational function but it never touches it actually.

10. What is an Oblique Asymptote?

It is a slant line which appears to touch the graph of the rational function but never touches it. It is present only in the case where degree of numerator N = degree of denominator D+1.

11. What are Applications of Rational Functions?

Rational functions are used in various real life scenarios such as business, medical and science.