Disentanglement in Beta Variational Autoencoders
Last Updated :
21 Sep, 2021
Beta Variational Autoencoders was proposed by researchers at Deepmind in 2017. It was accepted in the International Conference on Learning Representations (ICLR) 2017. Before learning Beta- variational autoencoder, please check out this article for variational autoencoder.
If in variational autoencoder, if each variable is sensitive to only one feature/ property of the dataset and relatively invariant to another property, then it is called disentangled representation of the dataset. The advantage of having a disentangled representation is that model is easy to generalize and has good interpretability. This is the main goal of beta variational autoencoders i.e to achieve disentanglement. For example, a neural network trained on the human faces to determine the gender of that person needs to capture different features of the face (such as face width, hair color, eyes color) in separate dimensions to ensure the disentanglement.
B-VAE adds a parameter B to the variational autoencoder that acts as balance b/w latent capacity of node and independent constraint with reconstruction accuracy. The motivation behind adding this hyper parameter is to maximize the probability of generating a real dataset while minimizing the probability of real to estimated data is small, under 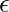 .
.
To write the equation below, we need to use the Kuhn-tucker condition.
![Rendered by QuickLaTeX.com \mathcal{F}\left(\theta, \phi, \beta; \mathbf{x}, \mathbf{z}\right) = \mathbb{E}_{q_{\phi}\left(\mathbf{z}|\mathbf{x}\right)}\left[\log{p}_{\theta}\left(\mathbf{x}\mid\mathbf{z}\right)\right] - \beta\left[D_{KL}\left(\log{q}_{\theta}\left(\mathbf{z}\mid\mathbf{x}\right)||p\left(\mathbf{z}\right)\right) - \epsilon\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2952a8bb42594611463bfdabfc5a492c_l3.png)
where the KKT multiplier 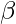 is the regularization coefficient that constrains the capacity of the latent channel z and puts implicit independence pressure on the learnt posterior due to the isotropic nature of the Gaussian prior p(z).
is the regularization coefficient that constrains the capacity of the latent channel z and puts implicit independence pressure on the learnt posterior due to the isotropic nature of the Gaussian prior p(z).
Now, we write this again using the above complementary slackness assumption to get the Beta-VAE formula:
![Rendered by QuickLaTeX.com \mathcal{F}\left(\theta, \phi, \beta; \mathbf{x}, \mathbf{z}\right) \geq \mathcal{L}\left(\theta, \phi, \beta; \mathbf{x}, \mathbf{z}\right) = \mathbb{E}_{q_{\phi}\left(\mathbf{z}|\mathbf{x}\right)}\left[\log{p}_{\theta}\left(\mathbf{x}\mid\mathbf{z}\right)\right] - \beta{D}_{KL}\left(\log{q}_{\theta}\left(\mathbf{z}\mid\mathbf{x}\right)||p\left(\mathbf{z}\right)\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72576b03ea1ccbf25fe1d9d23d48cf63_l3.png)
Beta-VAE attempts to learn a disentangled representation by conditionally independent data generative factors by optimizing a heavily penalizing KL-divergence between the prior and approximating distributions using a hyper parameter β > 1.
![Rendered by QuickLaTeX.com max_{\phi,\theta}E_{x \propto D}\left [ E_{z \sim q_{\phi}(z|x)} log p_{\theta} (x|z) \right ] \\ subject \, to \, D_{Kl}(q_{\phi}(z|x) || p_{\theta} (z) ) < \delta](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a908d03535315a3068332d1b2b17d330_l3.png)
We can rewrite the above equation with Lagrange multiplier Beta under kkT condition. The above equation is equal to following optimization condition:
Architecture:
The architecture Beta variational autoencoder has similar architecture when compared to variational autoencoder (except for the parameter beta). The complete setup contains two networks encoder and decoder. The encoder takes an image as input and generates the latent representation, whereas the decoder takes input that latent representation and tries to reconstruct the image. Here, latent representations are represented by the normal distribution that contains two variables — mean and variance. But the decoder requires only one latent representation. This is done by sampling from the normal distribution.

Beta-VAE architecture
Disentanglement in B-VAE:
The B-VAE is closely related to the InfoGAIN principle, which means the maximum information that can be stored is:
![Rendered by QuickLaTeX.com max[I(Z;Y) - \beta I(Z;Y)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-427fd728fa229ea330616c36bcbef4b6_l3.png)
where, I is mutual information and beta is the Lagrange multiplier, here the goal of this function is to maximize the latent information b/w latent bottleneck Z and task Y while discarding all the irrelevant information about Y that might be present in the input.
The authors experimented with the architecture by considering posterior distribution q(z|x) as an information bottleneck for the reconstruction task. They concluded that the posterior distribution efficiently transmits information about the data point x by minimizing the β-weighted KL term and maximizing the data log-likelihood.
In this VAE, the posterior distribution is encouraged to match the unit Gaussian prior (Normal distribution). Since the posterior and prior are factorized, the posterior can be calculated using the reparametrization trick, we can take an information-theory perspective and think of q(z|x) as a set of independent additive white Gaussian noise channels zi, each noisily transmitting information about the data inputs xn.
Now, the KL divergence term of the β-VAE objective 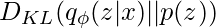 is an upper bound on the amount of information that can be transmitted through the latent channels per data sample. The KL divergence is zero when
is an upper bound on the amount of information that can be transmitted through the latent channels per data sample. The KL divergence is zero when
q(zi |x) = p(z), i.e µi is always zero, and σi is always 1, meaning the latent channels zi have zero capacity.
Thus, The capacity of the latent channels can only be increased by dispersing the posterior means across the data points or decreasing the posterior variances, which both increase the KL divergence term.
Share your thoughts in the comments
Please Login to comment...