5 variable K-Map in Digital Logic
Last Updated :
09 Jun, 2022
Prerequisite – Implicant in K-Map
Karnaugh Map or K-Map is an alternative way to write a truth table and is used for the simplification of Boolean Expressions. So far we are familiar with 3 variable K-Map & 4 variable K-Map. Now, let us discuss the 5-variable K-Map in detail. Any Boolean Expression or Function comprising of 5 variables can be solved using the 5 variable K-Map. A K-map for a 5-variable expression can be denoted with two 4-variable maps one beside the other. Such a 5 variable K-Map must contain
*** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
25= 32 cells to fill each minterm. As the number of variables keeps increasing, the efficacy of the Karnaugh map decreases. Let the 5-variable Boolean function be represented as
f ( P Q R S T) where P, Q, R, S, and T are the variables and P is the most significant bit variable and T is the least significant bit variable. The structure of such a K-Map for SOP expression is given below :

Cell no. written corresponding to each cell can be understood from the example described here:

Here for variable P=0, we have Q = 0, R = 1, S = 1, T = 1 i.e. (PQRST)=(00111) . In decimal form, this is equivalent to 7. So, for the cell shown above the corresponding cell no. = 7. In a similar manner, we can write cell numbers corresponding to every cell as shown in the above figure. Now let us discuss how to use a 5 variable K-Map to minimize a Boolean Function.
Rules to be followed:
- If a function is given in compact canonical SOP(Sum of Products) form then we write “1” corresponding to each minterm ( provided in the question ) in the corresponding cell numbers. For eg: For
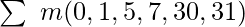 we will write “1” corresponding to cell numbers (0, 1, 5, 7, 30 and 31).
we will write “1” corresponding to cell numbers (0, 1, 5, 7, 30 and 31). - If a function is given in compact canonical POS(Product of Sums) form then we write “0” corresponding to each maxterm ( provided in the question ) in the corresponding cell numbers. For eg: For
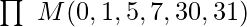 we will write “0” corresponding to cell numbers (0, 1, 5, 7, 30 and 31).
we will write “0” corresponding to cell numbers (0, 1, 5, 7, 30 and 31).
Steps to be followed:
- Make the largest possible size subcube covering all the marked 1’s in case of SOP or all marked 0’s in case of POS in the K-Map. It is important to note that each subcube can only contain terms in powers of 2 . Also a subcube of
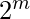 cells is possible if and only if in that subcube for every cell we satisfy that “m” number of cells are adjacent cells.
cells is possible if and only if in that subcube for every cell we satisfy that “m” number of cells are adjacent cells. - All Essential Prime Implicants (EPIs) must be present in the minimal expressions.
I. Solving SOP function: For clear understanding, let us solve the example of SOP function minimization of 5 Variable K-Map using the following expression : 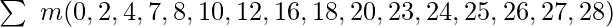
 In the above K-Map we have 4 subcubes:
In the above K-Map we have 4 subcubes:
- Subcube 1: The one marked in red comprises cells ( 0, 4, 8, 12, 16, 20, 24, 28)
- Subcube 2: The one marked in blue comprises cells (7, 23)
- Subcube 3: The one marked in pink comprises cells ( 0, 2, 8, 10, 16, 18, 24, 26)
- Subcube 4: The one marked in yellow comprises cells (24, 25, 26, 27)
Now, while writing the minimal expression of each of the subcubes we will search for the literal that is common to all the cells present in that subcube.
- Subcube 1:
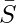 [Tex]\bar T [/Tex]
[Tex]\bar T [/Tex] - Subcube 2:
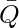 [Tex]R [/Tex]
[Tex]R [/Tex]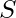 [Tex]T [/Tex]
[Tex]T [/Tex] - Subcube 3:
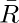 [Tex]\bar T [/Tex]
[Tex]\bar T [/Tex] - Subcube 4:
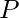 [Tex]Q [/Tex]
[Tex]Q [/Tex]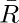
Finally the minimal expression of the given boolean Function can be expressed as follows : 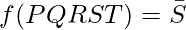 [Tex]\bar T [/Tex]
[Tex]\bar T [/Tex]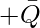 [Tex]R [/Tex]
[Tex]R [/Tex]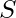 [Tex]T [/Tex]
[Tex]T [/Tex]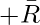 [Tex]\bar T [/Tex]
[Tex]\bar T [/Tex]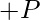 [Tex]Q [/Tex]
[Tex]Q [/Tex]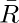
II. Solving POS function: Now, let us solve the example of POS function minimization of 5 Variable K-Map using the following expression : 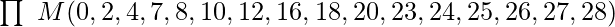
 In the above K-Map we have 4 subcubes:
In the above K-Map we have 4 subcubes:
- Subcube 1: The one marked in red comprises cells ( 0, 4, 8, 12, 16, 20, 24, 28)
- Subcube 2: The one marked in blue comprises cells (7, 23)
- Subcube 3: The one marked in pink comprises cells ( 0, 2, 8, 10, 16, 18, 24, 26)
- Subcube 4: The one marked in yellow comprises cells (24, 25, 26, 27)
Now, while writing the minimal expression of each of the subcubes we will search for the literal that is common to all the cells present in that subcube.
- Subcube 1:
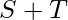
- Subcube 2:
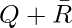 [Tex]+ \bar S [/Tex]
[Tex]+ \bar S [/Tex]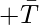
- Subcube 3:
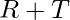
- Subcube 4:
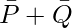 [Tex]+ R [/Tex]
[Tex]+ R [/Tex]
Finally the minimal expression of the given boolean Function can be expressed as follows : 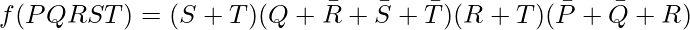
NOTE:
- For the 5 variable K-Map, the Range of the cell numbers will be from 0 to
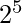 -1 i.e. 0 to 31.
-1 i.e. 0 to 31. - The above-mentioned term “Adjacent Cells” means “any two cells which differ in only 1 variable”.
Share your thoughts in the comments
Please Login to comment...