Logic gates are the fundamental components of all digital circuits and systems. In digital electronics, there are seven main types of logic gates used to perform various logical operations. A logic gate is basically an electronic circuit designed by using components like diodes, transistors, resistors, capacitors, etc., and capable of performing logical operations. In this article, we will study the definition, truth table, and other related concepts of logic gates. So let’s start with the basic introduction of logic gates.
What is a Logic Gate?
A logic gate is an electronic circuit designed by using electronic components like diodes, transistors, resistors, and more. As the name implies, a logic gate is designed to perform logical operations in digital systems like computers, communication systems, etc.
Therefore, we can say that the building blocks of a digital circuit are logic gates, which execute numerous logical operations that are required by any digital circuit. A logic gate can take two or more inputs but only produce one output. The output of a logic gate depends on the combination of inputs and the logical operation that the logic gate performs.
Logic gates use Boolean algebra to execute logical processes. Logic gates are found in nearly every digital gadget we use on a regular basis. Logic gates are used in the architecture of our telephones, laptops, tablets, and memory devices.
Types of Logic Gates
A logic gate is a digital gate that allows data to be manipulated. Logic gates, use logic to determine whether or not to pass a signal. Logic gates, on the other hand, govern the flow of information based on a set of rules.
The logic gates can be classified into the following major types:
1. Basic Logic Gates
There are three basic logic gates:
- AND Gate
- OR Gate
- NOT Gate
2. Universal Logic Gates
In digital electronics, the following two logic gates are considered as universal logic gates:
- NOR Gate
- NAND Gate
3. Derived Logic Gates
The following two are the derived logic gates used in digital systems:
- XOR Gate
- XNOR Gate
Let us now discuss each of these types of logic gates in detail one-by-one.
AND Gate
In digital electronics, the AND gate is one of the basic logic gate that performs the logical multiplication of inputs applied to it. It generates a high or logic 1 output, only when all the inputs applied to it are high or logic 1. Otherwise, the output of the AND gate is low or logic 0.
Properties of AND Gate:
The following are two main properties of the AND gate:
- AND gate can accept two or more than two input values at a time.
- When all of the inputs are logic 1, the output of this gate is logic 1.
The operation of an AND gate is described by a mathematical expression, which is called the Boolean expression of the AND gate.
For two-input AND gate, the Boolean expression is given by,
[Tex]Z = A.B
[/Tex]
Where, A and B are inputs to the AND gate, while Z denotes the output of the AND gate.
We can extend this expression to any number of input variables, such as,
[Tex]Z=A.B.C.D…
[/Tex]
Truth Table of AND Gate:
The truth table of a two input AND gate is given below:
Input
| Output
|
|---|
A
| B
| A AND B
|
0
| 0
| 0
|
0
| 1
| 0
|
1
| 0
| 0
|
1
| 1
| 1
|
Symbol of AND Gate:
The logic symbol of a two input AND gate is shown in the following figure.

Symbol of Two-Input AND Gate
OR Gate
In digital electronics, there is a type of basic logic gate which produces a low or logic 0 output only when its all inputs are low or logic 0. For all other input combinations, the output of the OR gate is high or logic 1. This logic gate is termed as OR gate. An OR gate can be designed to have two or more inputs but only one output. The primary function of the OR gate is to perform the logical sum operation.
Properties of OR Gate:
An OR gate have the following two properties:
- It can have two or more input lines at a time.
- When all of the inputs to the OR gate are low or logic 0, the output of it is low or logic 0.
The operation of an OR gate can be mathematically described through a mathematical expression called Boolean expression of the OR gate.
The boolean expression for a two input OR gate is given by,
Z = A + B
The boolean expression for a three-input OR gate is,
Z = A + B + C
Here, A, B, and C are inputs and Z is the output variables. We can extend this boolean expression to any number of input variables.
Truth Table of OR Gate:
The truth table of an OR gate describes the relationship between inputs and output. The following is the truth table for the two-input OR gate:
Input
| Output
|
|---|
A
| B
| A OR B
|
0
| 0
| 0
|
0
| 1
| 1
|
1
| 0
| 1
|
1
| 1
| 1
|
Symbol of OR Gate:
The logic symbol of a two-input OR gate is shown in the following figure.

Symbol of Two-Input OR Gate
NOT Gate
In digital electronics, the NOT gate is another basic logic gate used to perform compliment of an input signal applied to it. It takes only one input and one output. The output of the NOT gate is complement of the input applied to it. Therefore, if we apply a low or logic 0 output to the NOT gate is gives a high or logic 1 output and vice-versa. The NOT gate is also known as inverter, as it performs the inversion operation.
Properties of NOT Gate:
- The output of a NOT gate is complement or inverse of the input applied to it.
- NOT gate takes only one output.
The logical operation of the NOT gate is described by its boolean expression, which is given below.
[Tex]Z= \overline{A}
[/Tex]
The bar over the input variable A represents the inversion operation.
Truth Table of OR Gate:
The truth table describes the relationship between input and output. The following is the truth table for the NOT gate:
Input
| Output
|
|---|
A
| NOT A
|
0
| 1
|
1
| 0
|
Symbol of NOT Gate
The logic circuit symbol of a NOT gate is shown in the following figure. Here, A is the input line and Z is the output line.

Symbol of NOT the Gate
NOR Gate
The NOR gate is a type of universal logic gate that can take two or more inputs but one output. It is basically a combination of two basic logic gates i.e., OR gate and NOT gate. Thus, it can be expressed as,
NOR Gate = OR Gate + NOT Gate
In other words, a NOR gate is an OR gate followed by a NOT gate.
Properties of NOR Gate:
The following are two important properties of NOR gate:
- A NOR gate can have two or more inputs and gives an output.
- A NOR gate gives a high or logic 1 output only when its all inputs are low or logic 0.
Similar to basic logic gates, we can describe the operation of a NOR gate using a mathematical equation called boolean expression of the NOR gate.
The boolean expression of a two input NOR gate is given below:
[Tex]C=\overline{A+B}
[/Tex]
We can extend this expression to any number of input variables.
In the above boolean expressions, the variables A and B are called input variables while the variable C is called the output variable.
Truth Table of NOR Gate:
The following is the truth table of a two-input NOR gate showing the relationship between its inputs and output:
Input
| Output
|
|---|
A
| B
| A NOR B
|
0
| 0
| 1
|
0
| 1
| 0
|
1
| 0
| 0
|
1
| 1
| 0
|

Symbol of the NOR Gate
NAND Gate
In digital electronics, the NAND gate is another type of universal logic gate used to perform logical operations. The NAND gate performs the inverted operation of the AND gate. Similar to NOR gate, the NAND gate can also have two or more input lines but only one output line.
The NAND gate is also represented as a combination of two basic logic gates namely, AND gate and NOT gate. Hence, it can be expressed as
NAND Gate = AND Gate + NOT Gate
Properties of NAND Gate:
The following are the two key properties of NAND gate:
- NAND gate can take two or more inputs at a time and produces one output based on the combination of inputs applied.
- NAND gate produces a low or logic 0 output only when its all inputs are high or logic 1.
We can describe the expression of NAND gate through a mathematical equation called its boolean expression. Here is the boolean expression of a two input NAND gate.
[Tex]C=\overline{AB}
[/Tex]
In this expression, A and B are the input variables and C is the output variable. We can extend this relation to any number of input variables like three, four, or more.
Truth Table of NAND Gate:
The truth table is a table of inputs and output that describes the operation of the NAND gate and shows the logical relationship between them:
Input
| Output
|
|---|
A
| B
| A NAND B
|
0
| 0
| 1
|
0
| 1
| 1
|
1
| 0
| 1
|
1
| 1
| 0
|
Symbol of NAND Gate:
The logic symbol of a NAND gate is represented as a AND gate with a bubble on its output end as depicted in the following figure. It is the symbol of a two-input NAND gate.

Symbol of NAND Gate
XOR Gate
In digital electronics, there is a specially designed logic gate named, XOR gate, which is used in digital circuits to perform modulo sum. It is also referred to as Exclusive OR gate or Ex-OR gate. The XOR gate can take only two inputs at a time and give an output. The output of the XOR gate is high or logic 1 only when its two inputs are dissimilar.
Properties of XOR Gate:
The following two are the main properties of the XOR gate:
- It can accept only two inputs at a time. There is nothing like a three or more input XOR gate.
- The output of the XOR gate is logic 1 or high, when its inputs are dissimilar.
The operation of the XOR gate can be described through a mathematical equation called its boolean expression. The following is the boolean expression for the output of the XOR gate.
[Tex]Z=A \oplus B
[/Tex]
Here, Z is the output variable, and A and B are the input variables.
This expression can also be written as follows:
[Tex]Z=A \overline{B}+\overline{A}B
[/Tex]
Truth Table of XOR Gate:
The truth table is a table of inputs and output that describe the relationship between them and the operation of the XOR gate for different input combinations. The truth table of the XOR gate is given below:
Input
| Output
|
|---|
A
| B
| A XOR B
|
0
| 0
| 0
|
0
| 1
| 1
|
1
| 0
| 1
|
1
| 1
| 0
|
Symbol of XOR Gate:
The logic symbol of an XOR gate is shown in the following figure.
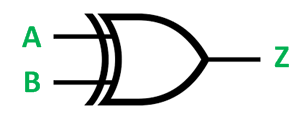
Symbol of XOR Gate
XNOR Gate
The XNOR gate is another type of special purpose logic gate used to implement exclusive operation in digital circuits. It is used to implement the Exclusive NOR operation in digital circuits. It is also called the Ex-NOR or Exclusive NOR gate. It is a combination of two logic gates namely, XOR gate and NOT gate. Thus, it can be expressed as,
XNOR Gate = XOR Gate + NOT Gate
The output of an XNOR gate is high or logic 1 when its both inputs are similar. Otherwise the output is low or logic 0. Hence, the XNOR gate is used as a similarity detector circuit.
Properties of XNOR Gate:
The following are two key properties of XNOR gate:
- XNOR gate takes only two inputs and produces one output.
- The output of the XNOR gate is high or logic 1 only when it has similar inputs.
The operation of XNOR gate can be described through a mathematical equation called the boolean expression of XNOR gate. Here is the boolean expression of the XNOR gate.
[Tex]Y=A \odot B
[/Tex]
We can also write this expression as follows:
[Tex]Y=AB + \overline{A} \overline{B}
[/Tex]
Here, the A and B are inputs and Y is the output.
Truth Table of XNOR Gate:
The truth table of the XNOR gate is given below. This truth table is describing the relationship between inputs and output of the XNOR gate.
Input
| Output
|
|---|
A
| B
| A XNOR B
|
0
| 0
| 1
|
0
| 1
| 0
|
1
| 0
| 0
|
1
| 1
| 1
|
Symbol of XNOR Gate:
The logic symbol of XNOR gate is shown in the following figure. Here, A and B are inputs and Y is the output.
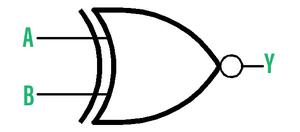
Symbol of XNOR gate
Applications of Logic Gates
Logic gates are the fundamental building blocks of all digital circuits and devices like computers. Here are some key digital devices in which logic gates are utilized to design their circuits:
- Computers
- Microprocessors
- Microcontrollers
- Digital and smart watches
- Smartphones, etc.
Based on Logic Gates – FAQs
What are Logic gates?
Logic gates are digital circuits that conduct logical operations on the input provided to them and produce appropriate output.
What are Universal gates?
To accomplish a specific logical process, universal gates are created by merging two or more fundamental gates. Universal gates are NAND and NOR gates.
What is the output of a NOT gate when input 0 is applied?
Because NOT gate is an inverter. As a result, if 0 is used as an input, the output will be 1.
Which logic gate is known as the “invertor”?
An invertor is also known as a NOT gate. The obtained output is the inverse of the input.
What is the Boolean expression for OR gate?
If A and B are the input, then the OR gate output can be given as Y=A+B.
What is the Boolean expression for the XNOR gate?
If A and B are the input, then the XNOR gate output can be given as Y=A.B+A’B’.
Share your thoughts in the comments
Please Login to comment...