Logic functions and Minimization

Question 1

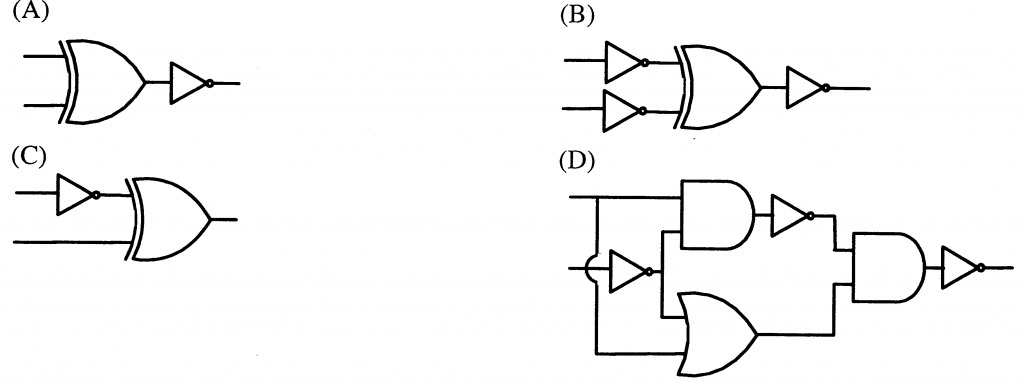
Which one of the following expressions does NOT represent exclusive NOR of x and y?

• A. xy+x'y'
• B. x⊕y'
• C. x'⊕y
• D. x'⊕y'

Answer: (D)

By Definition of XNOR, So Option-A is correct. Also by Definition of XOR, Option-B is So Option-B is also correct. Option-C is Option-C is also correct. Option-D x'⊕y' = x''y' + x'y'' = xy' + x'y = x⊕y ≠ x⊙y Therefore option (D) is false. This explanation is provided by Chirag Manwani.

Question 2

What is the minimal form of the Karnaugh map shown below? Assume that X denotes a don’t care term.

• A. b'd'
• B. b'd' + b'c'
• C. b'd' + a'b'c'd'
• D. b'd' + b'c' + c'd'

Answer: (B)

There are two prime implicants in the following K-Map- 

Prime Implicant highlighted in Green = 

Prime Implicant highlighted in Orange = 

So the Boolean expression is- 

Therefore option (B) is correct. 

Question 3

Which one of the following circuits is NOT equivalent to a 2-input XNOR (exclusive NOR) gate?

• A. A
• B. B
• C. C
• D. D

Answer: (D)

All options except D produce XOR as described below :

Question 4

The simplified SOP (Sum Of Product) form of the boolean expression (P + Q' + R') . (P + Q' + R) . (P + Q + R') is

• A. (P'.Q + R')
• B. (P + Q'.R')
• C. (P'.Q + R)
• D. (P.Q + R)

Answer: (B)

See following : (P+Q'+R').(P+Q'+R).(P+Q+R') = From the K-map, POS form is : P + Q'.R'

Question 5

The minterm expansion of f(P, Q, R) = PQ + QR' + PR' is

• A. m2 + m4 + m6 + m7
• B. m0 + m1 + m3 + m5
• C. m0 + m1 + m6 + m7
• D. m2 + m3 + m4 + m5

Answer: (A)

K-map,

= PQ + QR’ + PR’ 
= PQ(R+R’) + (P+P’)QR’ + P(Q+Q’)R’
= PQR + PQR’ +PQR’ +P’QR’ + PQR’ + PQ’R’ 
= PQR(m7) + PQR'(m6)+P’QR'(m2) +PQ’R'(m4) 
= m2 + m4 + m6 + m7 

Option (A) is correct.

Question 6

What is the minimum number of gates required to implement the Boolean function (AB+C)if we have to use only 2-input NOR gates?

• A. 2
• B. 3
• C. 4
• D. 5

Answer: (B)

AB+C = (A+C)(B+C) = ((A+C)' + (B+C)')' So, '3' 2-input NOR gates are required.

Question 7

In the Karnaugh map shown below, X denotes a don't care term. What is the minimal form of the function represented by the Karnaugh map?

A)   


B) 

C) 

D)  

• A. A
• B. B
• C. C
• D. D

Answer: (A)

One group consists of (0000, 0010, 1000, 1010) which gives b’d’ Other group is (0000, 0001, 1000, 1001) which gives a’d’ So, solution is b’d’ + a’d’

Question 8

Given f₁, f₃ and f in canonical sum of products form (in decimal) for the circuit

A) m(4, 6)

B) m(4, 8)

C) m(6, 8)

D) m(4, 6, 8)

• A. A
• B. B
• C. C
• D. D

Answer: (C)

From logic diagram  we have f=f1.f2+f3 f=m(4,5,6,7,8).f2+m(1,6,15)----(1) from eq(1) we need to find such f2 so that we can get  f=m(1,6,8,15) eq(1)  says we can get m(1,6,15) from f3 ,so only  8 left now from option (a,b,d) we get (4,6), (4,8) ,(4,6,8) respectively for m(4,5,6,7,8)f2 which is not required as m4 is undesired. But option (C) m(4,5,6,7,8)(6,8)+(1,6,15)

• m(6,8)+m(1,6,15)
• m(1,6,8,15)an

Option (C) is correct.

Question 9

If P, Q, R are Boolean variables, then (P + Q')(PQ' + PR)(P'R' + Q') simplifies

• A. PQ'
• B. PR'
• C. PQ' + R
• D. PR'' + Q

Answer: (A)

Step by step explanation :

= (P + Q’)(PQ’ + PR)(P’R’ + Q’)
= (PPQ’ + PPR + PQ’Q’ + PQ’R) (P’R’ + Q’) 
= (PQ’ + PR + PQ’ + PQ’R) (P’R’ + Q’)
= (PP’Q’R’ + PP’R’R + PP’Q’R’ + PP’Q’RR’ + PQ’Q’ + PQ’R + PQ’Q’ + PQ’Q’R)
= (0 + 0 + 0 + 0 + PQ’ + PQ’R + PQ’ + PQ’R)
= PQ’ + PQ’R
= PQ'(1 + R)
= PQ’ 

So, option (A) is correct.

Question 10

Consider the following Boolean function of four variables: f(w,x,y,z) = ∑(1,3,4,6,9,11,12,14) The function is:

• A. independent of one variables.
• B. independent of two variables.
• C. independent of three variables.
• D. dependent on all the variables.

Answer: (B)

On solving K-MAP we get ZX’+XZ’ so  it is independent of w,y Ans (B) part.