Full Subtractor in Digital Logic
Last Updated :
13 May, 2023
A full subtractor is a combinational circuit that performs subtraction of two bits, one is minuend and other is subtrahend, taking into account borrow of the previous adjacent lower minuend bit. This circuit has three inputs and two outputs. The three inputs A, B and Bin, denote the minuend, subtrahend, and previous borrow, respectively. The two outputs, D and Bout represent the difference and output borrow, respectively. Although subtraction is usually achieved by adding the complement of subtrahend to the minuend, it is of academic interest to work out the Truth Table and logic realisation of a full subtractor; x is the minuend; y is the subtrahend; z is the input borrow; D is the difference; and B denotes the output borrow. The corresponding maps for logic functions for outputs of the full subtractor namely difference and borrow.

Here’s how a full subtractor works:
1. First, we need to convert the binary numbers to their two’s complement form if we are subtracting a negative number.
2. Next, we compare the bits in the minuend and subtrahend at the corresponding positions. If the subtrahend bit is greater than or equal to the minuend bit, we need to borrow from the previous stage (if there is one) to subtract the subtrahend bit from the minuend bit.
3. We subtract the two bits along with the borrow-in to get the difference bit. If the minuend bit is greater than or equal to the subtrahend bit along with the borrow-in, then the difference bit is 1, otherwise it is 0.
4. We then calculate the borrow-out bit by comparing the minuend and subtrahend bits. If the minuend bit is less than the subtrahend bit along with the borrow-in, then we need to borrow for the next stage, so the borrow-out bit is 1, otherwise it is 0.
The circuit diagram for a full subtractor usually consists of two half-subtractors and an additional OR gate to calculate the borrow-out bit. The inputs and outputs of the full subtractor are as follows:
Inputs:
A: minuend bit
B: subtrahend bit
Bin: borrow-in bit from the previous stage
Outputs:
Diff: difference bit
Bout: borrow-out bit for the next stage
Truth Table –

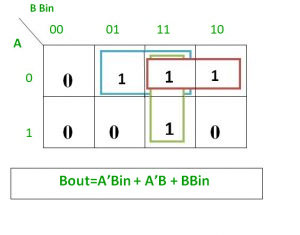
From above table we can draw the K-Map as shown for “difference” and “borrow”. 
Logical expression for difference –
D = A’B’Bin + A’BBin’ + AB’Bin’ + ABBin
= Bin(A’B’ + AB) + Bin’(AB’ + A’B)
= Bin( A XNOR B) + Bin’(A XOR B)
= Bin (A XOR B)’ + Bin’(A XOR B)
= Bin XOR (A XOR B)
= (A XOR B) XOR Bin
Logical expression for borrow –
Bout = A’B’Bin + A’BBin’ + A’BBin + ABBin
= A’B’Bin +A’BBin’ + A’BBin + A’BBin + A’BBin + ABBin
= A’Bin(B + B’) + A’B(Bin + Bin’) + BBin(A + A’)
= A’Bin + A’B + BBin
OR
Bout = A’B’Bin + A’BBin’ + A’BBin + ABBin
= Bin(AB + A’B’) + A’B(Bin + Bin’)
= Bin( A XNOR B) + A’B
= Bin (A XOR B)’ + A’B
Logic Circuit for Full Subtractor –

Implementation of Full Subtractor using Half Subtractors – 2 Half Subtractors and an OR gate is required to implement a Full Subtractor.

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...