Minimum number of swaps required to sort an array

Given an array of N distinct elements, find the minimum number of swaps required to sort the array.

Examples:

Input: {4, 3, 2, 1}
Output: 2
Explanation: Swap index 0 with 3 and 1 with 2 to form the sorted array {1, 2, 3, 4}

Input: {1, 5, 4, 3, 2}
Output: 2

Approach: To solve the problem follow the below idea:

This can be easily done by visualizing the problem as a graph. We will have N nodes and an edge directed from node i to node j if the element at the i’th index must be present at the j’th index in the sorted array.

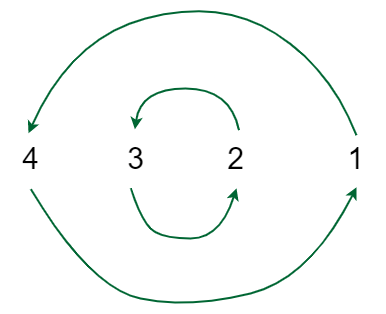
Graph for {4, 3, 2, 1}

The graph will now contain many non-intersecting cycles. Now a cycle with 2 nodes will only require 1 swap to reach the correct ordering, similarly, a cycle with 3 nodes will only require 2 swaps to do so. 

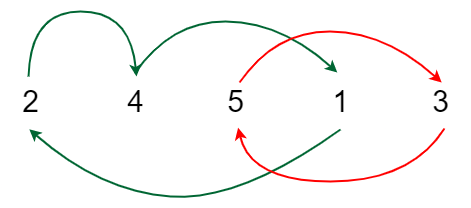
Graph for {4, 5, 2, 1, 3}

Hence, ans = Σ_{i = 1}^k(cycle_size – 1), where k is the number of cycles

Follow the below steps to solve the problem:

• Create an array of pairs arrPos to store the input array elements along with their index
• Sort arrPos and run a loop for i [0, N]
  • If the current element is already visited or it is at its correct position then continue
  • Else calculate the cycle size from the current element using a while loop
  • Declare an integer j equal to i and in the while loop set j equal to the index of arrPos[j] and increase cycle size while the element at jth position is not visited
• Increase the answer by the size of the current cycle – 1
• Return answer

Below is the implementation of the approach:

C

#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>

// structure to store element and its position
struct ElementPosition {
    int element;
    int position;
};

// function to find minimum number of swaps required to sort
// the array
int minSwaps(int arr[], int n)
{
    // create an array of ElementPosition structures
    struct ElementPosition arrPos[n];
    for (int i = 0; i < n; i++) {
        arrPos[i].element = arr[i];
        arrPos[i].position = i;
    }

    // sort the array by element values to get right
    // position of every element as second element of
    // structure
    for (int i = 0; i < n - 1; i++) {
        for (int j = i + 1; j < n; j++) {
            if (arrPos[i].element > arrPos[j].element) {
                struct ElementPosition temp = arrPos[i];
                arrPos[i] = arrPos[j];
                arrPos[j] = temp;
            }
        }
    }

    // initialize a boolean array to keep track of visited
    // elements
    bool vis[n];
    for (int i = 0; i < n; i++) {
        vis[i] = false;
    }

    // initialize result variable
    int ans = 0;

    // traverse array elements
    for (int i = 0; i < n; i++) {
        // already swapped and corrected or already present
        // at correct pos
        if (vis[i] || arrPos[i].position == i) {
            continue;
        }

        // find out the number of elements in this cycle and
        // add in ans
        int cycle_size = 0;
        int j = i;
        while (!vis[j]) {
            vis[j] = true;

            // move to next node
            j = arrPos[j].position;
            cycle_size++;
        }

        // update answer by adding current cycle
        if (cycle_size > 0) {
            ans += (cycle_size - 1);
        }
    }

    // return result
    return ans;
}

// driver code
int main()
{
    int arr[] = { 1, 5, 4, 3, 2 };
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("%d", minSwaps(arr, n));
    return 0;
}

C++

// C++ program to find
// minimum number of swaps
// required to sort an array
#include <bits/stdc++.h>
using namespace std;

// Function returns the
// minimum number of swaps
// required to sort the array
int minSwaps(int arr[], int n)
{
    // Create an array of
    // pairs where first
    // element is array element
    // and second element
    // is position of first element
    pair<int, int> arrPos[n];
    for (int i = 0; i < n; i++) {
        arrPos[i].first = arr[i];
        arrPos[i].second = i;
    }

    // Sort the array by array
    // element values to
    // get right position of
    // every element as second
    // element of pair.
    sort(arrPos, arrPos + n);

    // To keep track of visited elements.
    // Initialize
    // all elements as not visited or false.
    vector<bool> vis(n, false);

    // Initialize result
    int ans = 0;

    // Traverse array elements
    for (int i = 0; i < n; i++) {
        // already swapped and corrected or
        // already present at correct pos
        if (vis[i] || arrPos[i].second == i)
            continue;

        // find out the number of  node in
        // this cycle and add in ans
        int cycle_size = 0;
        int j = i;
        while (!vis[j]) {
            vis[j] = 1;

            // move to next node
            j = arrPos[j].second;
            cycle_size++;
        }

        // Update answer by adding current cycle.
        if (cycle_size > 0) {
            ans += (cycle_size - 1);
        }
    }

    // Return result
    return ans;
}

// Driver code
int main()
{
    int arr[] = { 1, 5, 4, 3, 2 };
    int n = (sizeof(arr) / sizeof(int));
    cout << minSwaps(arr, n);
    return 0;
}

Java

// Java program to find
// minimum number of swaps
// required to sort an array
import java.util.*;
import java.util.ArrayList;
import javafx.util.Pair;

class GfG {
    // Function returns the
    // minimum number of swaps
    // required to sort the array
    public static int minSwaps(int[] arr)
    {
        int n = arr.length;

        // Create two arrays and
        // use as pairs where first
        // array is element and second array
        // is position of first element
        ArrayList<Pair<Integer, Integer> > arrpos
            = new ArrayList<Pair<Integer, Integer> >();
        for (int i = 0; i < n; i++)
            arrpos.add(
                new Pair<Integer, Integer>(arr[i], i));

        // Sort the array by array element values to
        // get right position of every element as the
        // elements of second array.
        arrpos.sort(
            new Comparator<Pair<Integer, Integer> >() {
                @Override
                public int compare(
                    Pair<Integer, Integer> o1,
                    Pair<Integer, Integer> o2)
                {
                    if (o1.getKey() > o2.getKey())
                        return -1;

                    // We can change this to make
                    // it then look at the
                    // words alphabetical order
                    else if (o1.getKey().equals(
                                 o2.getKey()))
                        return 0;

                    else
                        return 1;
                }
            });

        // To keep track of visited elements. Initialize
        // all elements as not visited or false.
        Boolean[] vis = new Boolean[n];
        Arrays.fill(vis, false);

        // Initialize result
        int ans = 0;

        // Traverse array elements
        for (int i = 0; i < n; i++) {
            // already swapped and corrected or
            // already present at correct pos
            if (vis[i] || arrpos.get(i).getValue() == i)
                continue;

            // find out the number of  node in
            // this cycle and add in ans
            int cycle_size = 0;
            int j = i;
            while (!vis[j]) {
                vis[j] = true;

                // move to next node
                j = arrpos.get(j).getValue();
                cycle_size++;
            }

            // Update answer by adding current cycle.
            if (cycle_size > 0) {
                ans += (cycle_size - 1);
            }
        }

        // Return result
        return ans;
    }
}

class MinSwaps {
    // Driver code
    public static void main(String[] args)
    {
        int[] a = { 1, 5, 4, 3, 2 };
        GfG g = new GfG();
        System.out.println(g.minSwaps(a));
    }
}
// This code is contributed by Saksham Seth

Python3

# Python3 program to find
# minimum number of swaps
# required to sort an array

# Function returns the minimum
# number of swaps required to
# sort the array


def minSwaps(arr):
    n = len(arr)

    # Create two arrays and use
    # as pairs where first array
    # is element and second array
    # is position of first element
    arrpos = [*enumerate(arr)]

    # Sort the array by array element
    # values to get right position of
    # every element as the elements
    # of second array.
    arrpos.sort(key=lambda it: it[1])

    # To keep track of visited elements.
    # Initialize all elements as not
    # visited or false.
    vis = {k: False for k in range(n)}

    # Initialize result
    ans = 0
    for i in range(n):

        # already swapped or
        # already present at
        # correct position
        if vis[i] or arrpos[i][0] == i:
            continue

        # find number of nodes
        # in this cycle and
        # add it to ans
        cycle_size = 0
        j = i

        while not vis[j]:

            # mark node as visited
            vis[j] = True

            # move to next node
            j = arrpos[j][0]
            cycle_size += 1

        # update answer by adding
        # current cycle
        if cycle_size > 0:
            ans += (cycle_size - 1)

    # return answer
    return ans


# Driver Code
arr = [1, 5, 4, 3, 2]
print(minSwaps(arr))

# This code is contributed
# by Dharan Aditya

C#

// C# program to find
// minimum number of swaps
// required to sort an array
using System;
using System.Collections.Generic;
using System.Linq;

public class GfG {

    // Function returns the
    // minimum number of swaps
    // required to sort the array
    public int minSwaps(int[] arr)
    {
        int n = arr.Length;

        // Create two arrays and
        // use as pairs where first
        // array is element and second array
        // is position of first element
        List<KeyValuePair<int, int> > arrpos
            = new List<KeyValuePair<int, int> >();
        for (int i = 0; i < n; i++)
            arrpos.Add(
                new KeyValuePair<int, int>(arr[i], i));

        // Sort the array by array element values to
        // get right position of every element as the
        // elements of second array.
        arrpos.Sort((a, b) = > a.Key - b.Key);

        // To keep track of visited elements. Initialize
        // all elements as not visited or false.
        Boolean[] vis = new Boolean[n];

        // Initialize result
        int ans = 0;

        // Traverse array elements
        for (int i = 0; i < n; i++) {

            // already swapped and corrected or
            // already present at correct pos
            if (vis[i] || arrpos[i].Value == i)
                continue;

            // find out the number of  node in
            // this cycle and add in ans
            int cycle_size = 0;
            int j = i;
            while (!vis[j]) {
                vis[j] = true;

                // move to next node
                j = arrpos[j].Value;
                cycle_size++;
            }

            // Update answer by adding current cycle.
            if (cycle_size > 0) {
                ans += (cycle_size - 1);
            }
        }

        // Return result
        return ans;
    }
}

// Driver class
public class MinSwaps {
    // Driver program to test the above function
    public static void Main(String[] args)
    {
        int[] a = { 1, 5, 4, 3, 2 };
        GfG g = new GfG();
        Console.WriteLine(g.minSwaps(a));
    }
}

// This code is contributed by Rajput-Ji

Javascript

<script>

// JavaScript program to find
// minimum number of swaps
// required to sort an array

// Function returns the
// minimum number of swaps
// required to sort the array
function minSwaps(arr)
{
    let n = arr.length;

        // Create two arrays and
        // use as pairs where first
        // array is element and second array
        // is position of first element
        let arrpos = [];
        for (let i = 0; i < n; i++)
             arrpos.push([arr[i], i]);

        // Sort the array by array element values to
        // get right position of every element as the
        // elements of second array.
        arrpos.sort(function(a,b){return a[0]-b[0];});

        // To keep track of visited elements. Initialize
        // all elements as not visited or false.
        let vis = new Array(n);
        for(let i=0;i<n;i++)
        {
            vis[i]=false;
        }


        // Initialize result
        let ans = 0;

        // Traverse array elements
        for (let i = 0; i < n; i++)
        {
            // already swapped and corrected or
            // already present at correct pos
            if (vis[i] || arrpos[i][1] == i)
                continue;

            // find out the number of  node in
            // this cycle and add in ans
            let cycle_size = 0;
            let j = i;
            while (!vis[j])
            {
                vis[j] = true;

                // move to next node

                j = arrpos[j][1];

                cycle_size++;
            }

            // Update answer by adding current cycle.
            if(cycle_size > 0)
            {
                ans += (cycle_size - 1);
            }
        }

        // Return result
        return ans;
}

// Driver class
let a=[1, 5, 4, 3, 2];
document.write(minSwaps(a))

// This code is contributed by ab2127

</script>

Output

2

Time Complexity: O(N * Log N) 
Auxiliary Space: O(N)

Note: As the Pair class is available in java from java 8 so we can use hashmap in the older java version, so instead of using an ArrayList of pairs in java, we can use hashmap, rest of the steps remain the same.

Below is the implementation of the above approach: 

C

#include <stdio.h>
#include <stdlib.h>

// Comparator function for qsort
int cmpfunc(const void* a, const void* b)
{
    return (*(int*)a - *(int*)b);
}

// Function returns the
// minimum number of swaps
// required to sort the array
int minSwaps(int nums[], int n)
{
    int len = n;
    int map[100001] = { 0 };
    for (int i = 0; i < len; i++)
        map[nums[i]] = i;

    qsort(nums, n, sizeof(int), cmpfunc);

    // To keep track of visited elements. Initialize
    // all elements as not visited or false.
    int visited[len];
    memset(visited, 0, len * sizeof(int));

    // Initialize result
    int ans = 0;
    for (int i = 0; i < len; i++) {

        // already swapped and corrected or
        // already present at correct pos
        if (visited[i] || map[nums[i]] == i)
            continue;

        int j = i, cycle_size = 0;
        while (!visited[j]) {
            visited[j] = 1;

            // move to next node
            j = map[nums[j]];
            cycle_size++;
        }

        // Update answer by adding current cycle.
        if (cycle_size > 0) {
            ans += (cycle_size - 1);
        }
    }
    return ans;
}

// Driver code
int main()
{
    // Driver program to test the above function
    int a[] = { 1, 5, 4, 3, 2 };
    int n = 5;
    printf("%d", minSwaps(a, n));
    return 0;
}

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;
// Function returns the
// minimum number of swaps
// required to sort the array
int minSwaps(int nums[], int n)
{
    int len = n;
    map<int, int> map;
    for (int i = 0; i < len; i++)
        map[nums[i]] = i;

    sort(nums, nums + n);

    // To keep track of visited elements. Initialize
    // all elements as not visited or false.
    bool visited[len] = { 0 };

    // Initialize result
    int ans = 0;
    for (int i = 0; i < len; i++) {

        // already swapped and corrected or
        // already present at correct pos
        if (visited[i] || map[nums[i]] == i)
            continue;

        int j = i, cycle_size = 0;
        while (!visited[j]) {
            visited[j] = true;

            // move to next node
            j = map[nums[j]];
            cycle_size++;
        }

        // Update answer by adding current cycle.
        if (cycle_size > 0) {
            ans += (cycle_size - 1);
        }
    }
    return ans;
}

// Driver code
int main()
{
    // Driver program to test the above function
    int a[] = { 1, 5, 4, 3, 2 };
    int n = 5;
    cout << minSwaps(a, n);
    return 0;
}

// This code is contributed by Harshal Khond

Java

// Java program for the above approach

import java.io.*;
import java.util.*;

class GfG {
    // Function returns the
    // minimum number of swaps
    // required to sort the array
    public static int minSwaps(int[] nums)
    {
        int len = nums.length;
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < len; i++)
            map.put(nums[i], i);

        Arrays.sort(nums);

        // To keep track of visited elements. Initialize
        // all elements as not visited or false.
        boolean[] visited = new boolean[len];
        Arrays.fill(visited, false);

        // Initialize result
        int ans = 0;
        for (int i = 0; i < len; i++) {

            // already swapped and corrected or
            // already present at correct pos
            if (visited[i] || map.get(nums[i]) == i)
                continue;

            int j = i, cycle_size = 0;
            while (!visited[j]) {
                visited[j] = true;

                // move to next node
                j = map.get(nums[j]);
                cycle_size++;
            }

            // Update answer by adding current cycle.
            if (cycle_size > 0) {
                ans += (cycle_size - 1);
            }
        }
        return ans;
    }
}

// Driver class
class MinSwaps {
    // Driver program to test the above function
    public static void main(String[] args)
    {
        int[] a = { 1, 5, 4, 3, 2 };
        GfG g = new GfG();
        System.out.println(g.minSwaps(a));
    }
}
// This code is contributed by Saurabh Johari

Python3

# Function returns the
# minimum number of swaps
# required to sort the array
from functools import cmp_to_key


def cmp(a, b):
    return a - b


def minSwaps(nums):
    Len = len(nums)
    map = {}
    for i in range(Len):
        map[nums[i]] = i

    nums = sorted(nums, key=cmp_to_key(cmp))

    # To keep track of visited elements. Initialize
    # all elements as not visited or false.
    visited = [False for col in range(Len)]

    # Initialize result
    ans = 0
    for i in range(Len):

        # already swapped and corrected or
        # already present at correct pos
        if (visited[i] or map[nums[i]] == i):
            continue

        j, cycle_size = i, 0
        while (visited[j] == False):
            visited[j] = True

            # move to next node
            j = map[nums[j]]
            cycle_size += 1

        # Update answer by adding current cycle.
        if (cycle_size > 0):
            ans += (cycle_size - 1)

    return ans


# Driver program to test the above function
a = [1, 5, 4, 3, 2]
print(minSwaps(a))

# This code is contributed by shinjanpatra

C#

// C# program for the above approach

using System;
using System.Collections.Generic;

class GfG {

    // Function returns the
    // minimum number of swaps
    // required to sort the array
    public int minSwaps(int[] nums)
    {
        int len = nums.Length;
        Dictionary<int, int> map
            = new Dictionary<int, int>();
        for (int i = 0; i < len; i++)
            map.Add(nums[i], i);

        Array.Sort(nums);

        // To keep track of visited elements. Initialize
        // all elements as not visited or false.
        bool[] visited = new bool[len];

        // Initialize result
        int ans = 0;
        for (int i = 0; i < len; i++) {

            // already swapped and corrected or
            // already present at correct pos
            if (visited[i] || map[nums[i]] == i)
                continue;

            int j = i, cycle_size = 0;
            while (!visited[j]) {
                visited[j] = true;

                // move to next node
                j = map[nums[j]];
                cycle_size++;
            }

            // Update answer by adding current cycle.
            if (cycle_size > 0) {
                ans += (cycle_size - 1);
            }
        }
        return ans;
    }
}

// Driver class
public class MinSwaps {

    // Driver program to test the above function
    public static void Main(String[] args)
    {
        int[] a = { 1, 5, 4, 3, 2 };
        GfG g = new GfG();
        Console.WriteLine(g.minSwaps(a));
    }
}

// This code is contributed by gauravrajput1

Javascript

<script>
    // Function returns the
    // minimum number of swaps
    // required to sort the array
    function minSwaps(nums) {
        var len = nums.length;
        var map = new Map();
        for (i = 0; i < len; i++)
            map.set(nums[i], i);

        nums.sort((a,b)=>a-b);

        // To keep track of visited elements. Initialize
        // all elements as not visited or false.
        var visited = Array(len).fill(false);

        // Initialize result
        var ans = 0;
        for (var i = 0; i < len; i++) {

            // already swapped and corrected or
            // already present at correct pos
            if (visited[i] || map.get(nums[i]) == i)
                continue;

            var j = i, cycle_size = 0;
            while (!visited[j]) {
                visited[j] = true;

                // move to next node
                j = map.get(nums[j]);
                cycle_size++;
            }

            // Update answer by adding current cycle.
            if (cycle_size > 0) {
                ans += (cycle_size - 1);
            }
        }
        return ans;
    }

    // Driver program to test the above function
        var a = [ 1, 5, 4, 3, 2 ];
        document.write(minSwaps(a));

// This code is contributed by Rajput-Ji
</script>

Output

2

Time Complexity: O(N Log N) 
Auxiliary Space: O(N)

The minimum number of swaps required to sort an array using a greedy algorithm: 

To solve the problem follow the below idea:

While iterating over the array, check the current element, and if not in the correct place, replace that element with the index of the element which should have come to this place greedily which will give the optimal answer

Follow the below steps to solve the problem:

• Create a new array and copy the elements of the input array
• Sort the new array and declare a variable ans equal to 0
• Run a for loop to traverse the elements
  • If the current element in the sorted array is not equal to the one in the input array then increase the and by 1
  • And swap the current element, with the required element at this index
• Return ans 

Below is the implementation of the above approach:

C

#include <stdio.h>
#include <stdlib.h>

void swap(int* arr, int i, int j)
{
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

int indexOf(int* arr, int size, int ele)
{
    for (int i = 0; i < size; i++) {
        if (arr[i] == ele) {
            return i;
        }
    }
    return -1;
}

int cmpfunc(const void* a, const void* b)
{
    return (*(int*)a - *(int*)b);
}

// Return the minimum number
// of swaps required to sort the array
int minSwaps(int* arr, int N)
{
    int ans = 0;
    int* temp = (int*)malloc(sizeof(int) * N);
    for (int i = 0; i < N; i++) {
        temp[i] = arr[i];
    }
    qsort(temp, N, sizeof(int), cmpfunc);

    for (int i = 0; i < N; i++) {

        // This is checking whether
        // the current element is
        // at the right place or not
        if (arr[i] != temp[i]) {
            ans++;

            // Swap the current element
            // with the right index
            // so that arr[0] to arr[i] is sorted
            swap(arr, i, indexOf(arr, N, temp[i]));
        }
    }
    return ans;
}

// Driver Code
int main()
{

    int a[] = { 101, 758, 315, 730, 472, 619, 460, 479 };

    int n = sizeof(a) / sizeof(a[0]);

    // Output will be 5
    printf("%d", minSwaps(a, n));
    return 0;
}

C++

// C++ program to find minimum number
// of swaps required to sort an array
#include <bits/stdc++.h>
using namespace std;

void swap(vector<int>& arr, int i, int j)
{
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

int indexOf(vector<int>& arr, int ele)
{
    for (int i = 0; i < arr.size(); i++) {
        if (arr[i] == ele) {
            return i;
        }
    }
    return -1;
}

// Return the minimum number
// of swaps required to sort the array
int minSwaps(vector<int> arr, int N)
{
    int ans = 0;
    vector<int> temp(arr.begin(), arr.end());
    sort(temp.begin(), temp.end());

    for (int i = 0; i < N; i++) {

        // This is checking whether
        // the current element is
        // at the right place or not
        if (arr[i] != temp[i]) {
            ans++;

            // Swap the current element
            // with the right index
            // so that arr[0] to arr[i] is sorted
            swap(arr, i, indexOf(arr, temp[i]));
        }
    }
    return ans;
}

// Driver Code
int main()
{

    vector<int> a
        = { 101, 758, 315, 730, 472, 619, 460, 479 };

    int n = a.size();

    // Output will be 5
    cout << minSwaps(a, n);
}

// This code is contributed by mohit kumar 29

Java

// Java program to find
// minimum number of swaps
// required to sort an array
import java.io.*;
import java.util.*;

class GfG {

    // Return the minimum number
    // of swaps required to sort the array
    public int minSwaps(int[] arr, int N)
    {
        int ans = 0;
        int[] temp = Arrays.copyOfRange(arr, 0, N);
        Arrays.sort(temp);
        for (int i = 0; i < N; i++) {

            // This is checking whether
            // the current element is
            // at the right place or not
            if (arr[i] != temp[i]) {
                ans++;

                // Swap the current element
                // with the right index
                // so that arr[0] to arr[i] is sorted
                swap(arr, i, indexOf(arr, temp[i]));
            }
        }
        return ans;
    }
    public void swap(int[] arr, int i, int j)
    {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    public int indexOf(int[] arr, int ele)
    {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == ele) {
                return i;
            }
        }
        return -1;
    }
}
// Driver class
class Main {

    // Driver program to test
    // the above function
    public static void main(String[] args) throws Exception
    {
        int[] a
            = { 101, 758, 315, 730, 472, 619, 460, 479 };
        int n = a.length;
        // Output will be 5
        System.out.println(new GfG().minSwaps(a, n));
    }
}
// This code is contributed by Satvik Nema

Python3

# Python3 program to find
# minimum number of swaps
# required to sort an array

# Return the minimum number
# of swaps required to sort
# the array


def minSwaps(arr, N):

    ans = 0
    temp = arr.copy()
    temp.sort()
    for i in range(N):

        # This is checking whether
        # the current element is
        # at the right place or not
        if (arr[i] != temp[i]):
            ans += 1

            # Swap the current element
            # with the right index
            # so that arr[0] to arr[i]
            # is sorted
            swap(arr, i,
                 indexOf(arr, temp[i]))

    return ans


def swap(arr, i, j):

    temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp


def indexOf(arr, ele):

    for i in range(len(arr)):
        if (arr[i] == ele):
            return i
    return -1


# Driver code
if __name__ == "__main__":
    a = [101, 758, 315, 730,
         472, 619, 460, 479]
    n = len(a)

    # Output will be 5
    print(minSwaps(a, n))

# This code is contributed by Chitranayal

C#

// C# program to find
// minimum number of swaps
// required to sort an array
using System;
public class GFG {

    // Return the minimum number
    // of swaps required to sort the array
    static int minSwaps(int[] arr, int N)
    {
        int ans = 0;
        int[] temp = new int[N];
        Array.Copy(arr, temp, N);
        Array.Sort(temp);
        for (int i = 0; i < N; i++) {

            // This is checking whether
            // the current element is
            // at the right place or not
            if (arr[i] != temp[i]) {
                ans++;

                // Swap the current element
                // with the right index
                // so that arr[0] to arr[i] is sorted
                swap(arr, i, indexOf(arr, temp[i]));
            }
        }
        return ans;
    }

    static void swap(int[] arr, int i, int j)
    {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    static int indexOf(int[] arr, int ele)
    {
        for (int i = 0; i < arr.Length; i++) {
            if (arr[i] == ele) {
                return i;
            }
        }
        return -1;
    }

    // Driver program to test
    // the above function
    static public void Main()
    {
        int[] a
            = { 101, 758, 315, 730, 472, 619, 460, 479 };
        int n = a.Length;
        // Output will be 5
        Console.WriteLine(minSwaps(a, n));
    }
}

// This code is contributed by rag2127

Javascript

<script>
// Javascript program to find
// minimum number of swaps
// required to sort an array

    // Return the minimum number
    // of swaps required to sort the array
    function minSwaps(arr,N)
    {
        let ans = 0;
        let temp = [...arr];
        temp.sort(function(a,b){return a-b;});
        for (let i = 0; i < N; i++)
        {

            // This is checking whether
            // the current element is
            // at the right place or not
            if (arr[i] != temp[i])
            {
                ans++;

                // Swap the current element
                // with the right index
                // so that arr[0] to arr[i] is sorted
                swap(arr, i, indexOf(arr, temp[i]));
            }
        }
        return ans;
    }

    function swap(arr,i,j)
    {
         let temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    function indexOf(arr,ele)
    {
        for (let i = 0; i < arr.length; i++)
        {
            if (arr[i] == ele) {
                return i;
            }
        }
        return -1;
    }

    // Driver class
    let a=[101, 758, 315, 730, 472,
                         619, 460, 479 ];
    let n = a.length;
    document.write(minSwaps(a, n));


    // This code is contributed by unknown2108
</script>

Output

5

Time Complexity: O(N²) 
Auxiliary Space: O(N)

Note: We can still improve the complexity by using a hashmap. The main operation here is the indexOf method inside the loop, which costs us n*n. We can improve this section to O(n), by using a hashmap to store the indexes. Still, we use the sort method, so the complexity cannot improve beyond O(n Log n)

The minimum number of swaps required to sort an array using Hash-Map: 

Follow the below steps to solve the problem:

• Make a new array (called temp), which is the sorted form of the input array. We know that we need to transform the input array to the new array (temp) in the minimum number of swaps. 
• Make a map that stores the elements and their corresponding index, of the input array.
• So at each i starting from 0 to N in the given array, where N is the size of the array:
  • If i is not in its correct position according to the sorted array, then
  • We will fill this position with the correct element from the hashmap we built earlier. We know the correct element which should come here is temp[i], so we look up the index of this element from the hashmap. 
  • After swapping the required elements, we update the content of the hashmap accordingly, as temp[i] to the ith position, and arr[i] to where temp[i] was earlier
• Return answer

Below is the implementation of the above approach:

C

#include <stdio.h>
#include <stdlib.h>

void swap(int* arr, int i, int j)
{
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

int cmpfunc(const void* a, const void* b)
{
    return (*(int*)a - *(int*)b);
}

// Return the minimum number
// of swaps required to sort
// the array
int minSwaps(int arr[], int N)
{
    int ans = 0;
    int temp[N];
    for (int i = 0; i < N; i++) {
        temp[i] = arr[i];
    }

    // Hashmap which stores the
    // indexes of the input array
    int h[N];
    for (int i = 0; i < N; i++) {
        h[arr[i]] = i;
    }

    // Sort the temp array
    qsort(temp, N, sizeof(int), cmpfunc);

    for (int i = 0; i < N; i++) {
        // This is checking whether
        // the current element is
        // at the right place or not
        if (arr[i] != temp[i]) {
            ans++;
            int init = arr[i];

            // If not, swap this element
            // with the index of the
            // element which should come here
            swap(arr, i, h[temp[i]]);

            // Update the indexes in
            // the hashmap accordingly
            h[init] = h[temp[i]];
            h[temp[i]] = i;
        }
    }
    return ans;
}

// Driver code
int main()
{
    int a[] = { 101, 758, 315, 730, 472, 619, 460, 479 };
    int n = sizeof(a) / sizeof(int);

    printf("%d", minSwaps(a, n));
    return 0;
}

C++

// C++ program to find
// minimum number of swaps
// required to sort an array
#include <bits/stdc++.h>
using namespace std;

void swap(vector<int>& arr, int i, int j)
{
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
// Return the minimum number
// of swaps required to sort
// the array
int minSwaps(vector<int> arr, int N)
{
    int ans = 0;
    vector<int> temp = arr;

    // Hashmap which stores the
    // indexes of the input array
    map<int, int> h;

    sort(temp.begin(), temp.end());
    for (int i = 0; i < N; i++) {
        h[arr[i]] = i;
    }
    for (int i = 0; i < N; i++) {
        // This is checking whether
        // the current element is
        // at the right place or not
        if (arr[i] != temp[i]) {
            ans++;
            int init = arr[i];

            // If not, swap this element
            // with the index of the
            // element which should come here
            swap(arr, i, h[temp[i]]);

            // Update the indexes in
            // the hashmap accordingly
            h[init] = h[temp[i]];
            h[temp[i]] = i;
        }
    }
    return ans;
}

// Driver code
int main()
{
    vector<int> a
        = { 101, 758, 315, 730, 472, 619, 460, 479 };
    int n = a.size();

    cout << minSwaps(a, n);
}

// This code is contributed by Stream_Cipher

Java

// Java program to find
// minimum number of swaps
// required to sort an array
import java.io.*;
import java.util.*;

class GfG {

    // Return the minimum number
    // of swaps required to sort the array
    public int minSwaps(int[] arr, int N)
    {

        int ans = 0;
        int[] temp = Arrays.copyOfRange(arr, 0, N);

        // Hashmap which stores the
        // indexes of the input array
        HashMap<Integer, Integer> h
            = new HashMap<Integer, Integer>();

        Arrays.sort(temp);
        for (int i = 0; i < N; i++) {
            h.put(arr[i], i);
        }
        for (int i = 0; i < N; i++) {

            // This is checking whether
            // the current element is
            // at the right place or not
            if (arr[i] != temp[i]) {
                ans++;
                int init = arr[i];

                // If not, swap this element
                // with the index of the
                // element which should come here
                swap(arr, i, h.get(temp[i]));

                // Update the indexes in
                // the hashmap accordingly
                h.put(init, h.get(temp[i]));
                h.put(temp[i], i);
            }
        }
        return ans;
    }
    public void swap(int[] arr, int i, int j)
    {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

// Driver code
class Main {


    public static void main(String[] args) throws Exception
    {
        int[] a
            = { 101, 758, 315, 730, 472, 619, 460, 479 };
        int n = a.length;

        System.out.println(new GfG().minSwaps(a, n));
    }
}
// This code is contributed by Satvik Nema

Python3

# Python3 program to find
# minimum number of swaps
# required to sort an array

# Return the minimum number
# of swaps required to sort
# the array


def minSwap(arr, n):

    ans = 0
    temp = arr.copy()

    # Dictionary which stores the
    # indexes of the input array
    h = {}

    temp.sort()

    for i in range(n):

        # h.[arr[i]
        h[arr[i]] = i

    init = 0

    for i in range(n):

        # This is checking whether
        # the current element is
        # at the right place or not
        if (arr[i] != temp[i]):
            ans += 1
            init = arr[i]

            # If not, swap this element
            # with the index of the
            # element which should come here
            arr[i], arr[h[temp[i]]] = arr[h[temp[i]]], arr[i]

            # Update the indexes in
            # the hashmap accordingly
            h[init] = h[temp[i]]
            h[temp[i]] = i

    return ans


# Driver code
a = [101, 758, 315, 730,
     472, 619, 460, 479]
n = len(a)


print(minSwap(a, n))

# This code is contributed by avanitrachhadiya2155

C#

// C# program to find
// minimum number of swaps
// required to sort an array
using System;
using System.Collections.Generic;
using System.Linq;
public class GfG {

    // Return the minimum number
    // of swaps required to sort the array
    public int minSwaps(int[] arr, int N)
    {

        int ans = 0;
        int[] temp = new int[N];
        arr.CopyTo(temp, 0);

        // Hashmap which stores the
        // indexes of the input array
        Dictionary<int, int> h = new Dictionary<int, int>();

        Array.Sort(temp);
        for (int i = 0; i < N; i++) {
            h.Add(arr[i], i);
        }
        for (int i = 0; i < N; i++) {

            // This is checking whether
            // the current element is
            // at the right place or not
            if (arr[i] != temp[i]) {
                ans++;
                int init = arr[i];

                // If not, swap this element
                // with the index of the
                // element which should come here
                swap(arr, i, h[temp[i]]);

                // Update the indexes in
                // the hashmap accordingly
                h[init] = h[temp[i]];
                h[temp[i]] = i;
            }
        }
        return ans;
    }

    public void swap(int[] arr, int i, int j)
    {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

// Driver code
public class GFG {

    public static void Main(String[] args)
    {
        int[] a
            = { 101, 758, 315, 730, 472, 619, 460, 479 };
        int n = a.Length;

        Console.WriteLine(new GfG().minSwaps(a, n));
    }
}

// This code is contributed by Rajput-Ji

Javascript

<script>

// JavaScript program to find
// minimum number of swaps
// required to sort an array
function swap(arr, i, j)
{
  let temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}

// Return the minimum number
// of swaps required to sort
// the array
function minSwaps(arr,N)
{
  let ans = 0;
  let temp = arr.slice();

  // Hashmap which stores the
  // indexes of the input array
  let h = new Map();

  temp.sort();
  for (let i = 0; i < N; i++)
  {
    h.set(arr[i], i);
  }
  for (let i = 0; i < N; i++)
  {

    // This is checking whether
    // the current element is
    // at the right place or not
    if (arr[i] != temp[i])
    {
      ans++;
      let init = arr[i];

      // If not, swap this element
      // with the index of the
      // element which should come here
      swap(arr, i, h.get(temp[i]));

      // Update the indexes in
      // the hashmap accordingly
      h.set(init,h.get(temp[i]));
      h.set(temp[i],i);
    }
  }
  return ans;
}

// Driver class

  // Driver program to
  // test the above function
let a = [101, 758, 315, 730, 472, 619, 460, 479];
let n = a.length;

// Output will be 5
document.write(minSwaps(a, n));

// This code is contributed by shinjanpatra

</script>

Output

5

Time Complexity: O(N * Log N) 
Auxiliary Space: O(N)

This article is contributed by Ayush Khanduri. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.