Data Structures and Algorithms | Set 36
Last Updated :
06 Feb, 2018
Que – 1. The function shiftNode() which takes as input two linked lists- destination and source. It deletes front node from source and places it onto the front of destination. Choose the set of statements which replace X, Y, Z in given function.
void shiftNode(struct node** destRoot,
struct node** srcRoot)
{
// the front of source node
struct node* newNode = *srcRoot;
assert(newNode != NULL);
X;
Y;
Z;
}
(A)
X: *srcRoot = newNode->next
Y: newNode->next = *destRoot->next
Z: *destRoot->next = newNode
(B)
X: *srcRoot->next = newNode->next
Y: newNode->next = *destRoot
Z: *destRoot = newNode->next
(C)
X: *srcRoot = newNode->next
Y: newNode->next = *destRoot
Z: *destRoot = srcRoot->next
(D)
X: *srcRoot = newNode->next
Y: newNode->next = *destRoot
Z: *destRoot = newNode
Solution:
X: Move forward the pointer to source linked list.
Y: Make the new node point to the front of the old destination linked list.
Z: Let the destination linked list point to the new node.
So, option (D) is correct.
Que – 2. A vertex v is said to be “over” when the recursion DFS(v) finishes. What is the order of the vertices being “over” for the given graph? Consider the DFS to begin at vertex a and in case of multiple possible paths, travel in an alphabetical manner.

(A) e f i h g c d b a
(B) a b d c e g f h i
(C) a b c d e g i f h
(D) e f i h d g c b a
Solution:
It is important to note here that the answer is NOT the DFS of the graph. The nodes in pink give the order of DFS. That is: a b d c e g f h i. The nodes in green give the order in which they keep getting “over”: e f i h g c d b a.
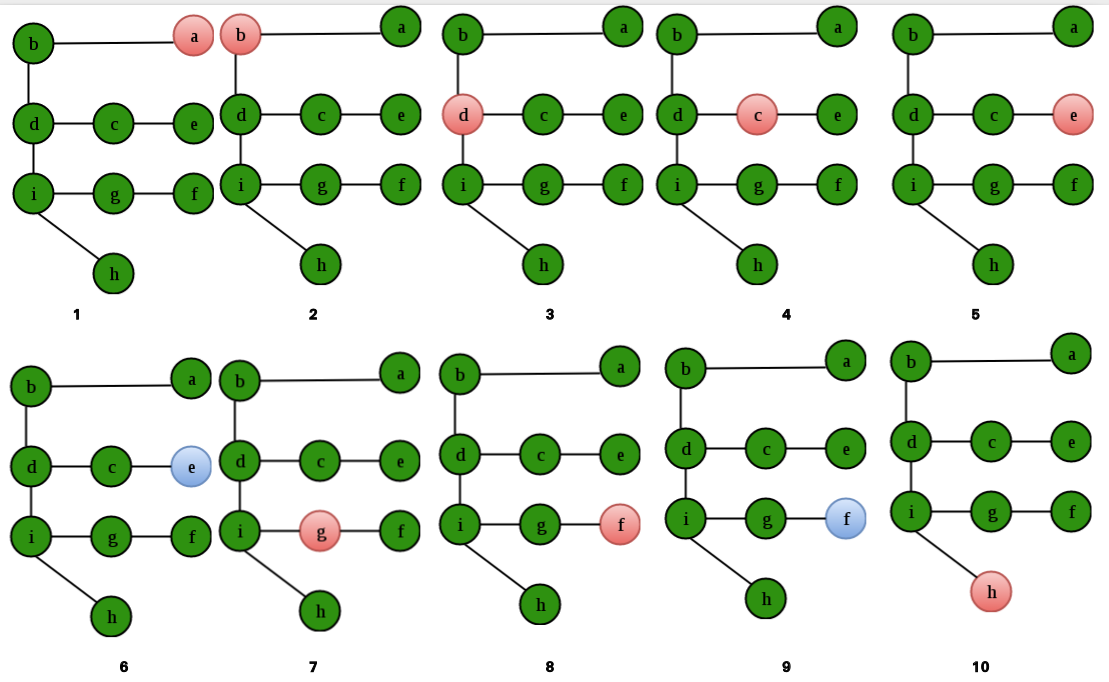
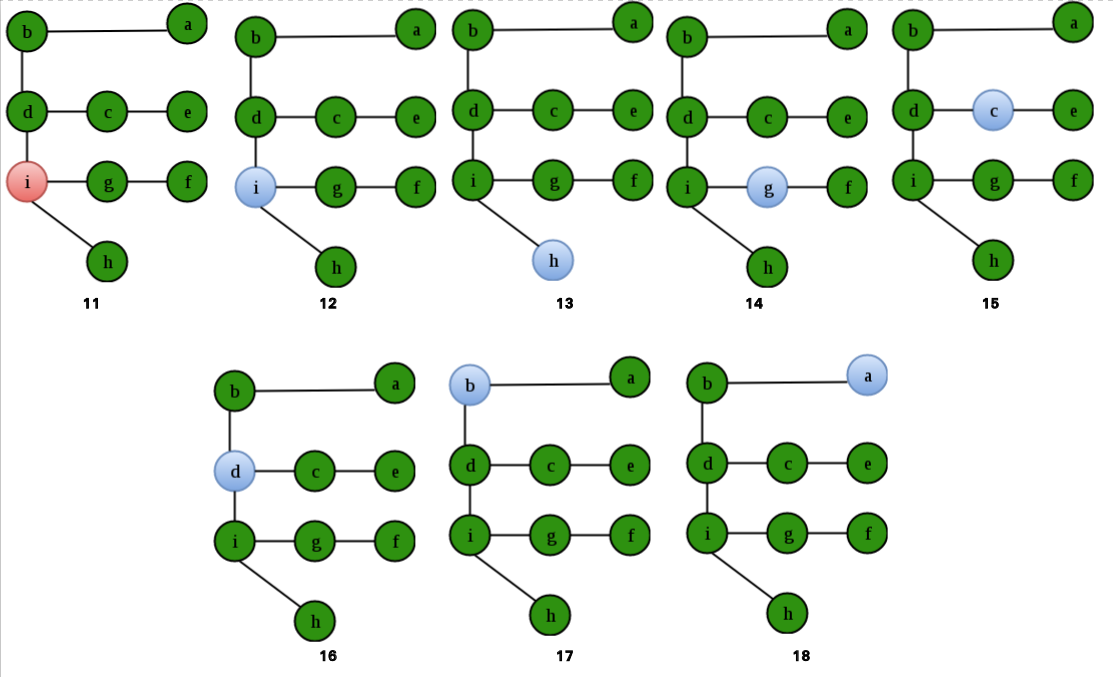
Option (A) is correct.
Que – 3. You are given two singly linked lists with heads head_ref1 and head_ref2 respectively. What does the following function do?
int myFunc(Node* head_ref1, Node* head_ref2) {
Node *pointer1 = head_ref1, *pointer2 = head_ref2;
while (pointer1 != pointer2) {
pointer1 = pointer1?pointer1->next:head_ref2;
pointer2 = pointer2?pointer2->next:head_ref1;
}
return pointer1?pointer1->data:-1;
}
(A) Merging the two linked lists
(B) Finding the merging point of the two linked lists
(C) Swapping nodes of the two linked lists
(D) The program runs in an infinite loop
Solution:
The pointers to both the linked lists keep incrementing and exchanging between lists until they find a common point of intersection. The function returns -1 if there is no merge point i.e. when pointer1 and pointer2 meet at NULL. Performing a dry run on sample linked lists would make the concept clearer.
Option (B) is correct.
Que – 4. The function copyBSTNodes() creates a copy of each node of a Binary Search Tree and inserts the copied node as the left child of the original node. The resultant tree remains a BST. Choose the set of statements which replace X and Y in given function.
void copyBSTNodes (struct node* root) {
struct node* prevLeft;
if (root==NULL) return;
copyBSTNodes (root->left);
copyBSTNodes (root->right);
X;
root->left = newNode(root->data);
Y;
}
(A)
X: prevLeft->left = root->left
Y: root->left->left = prevLeft->left
(B)
X: prevLeft = root->left
Y: root->left->left = prevLeft
(C)
X: prevLeft = root
Y: root->left = prevLeft
(d)
X: prevLeft = root->left
Y: root->left->left = prevLeft->left
Solution:
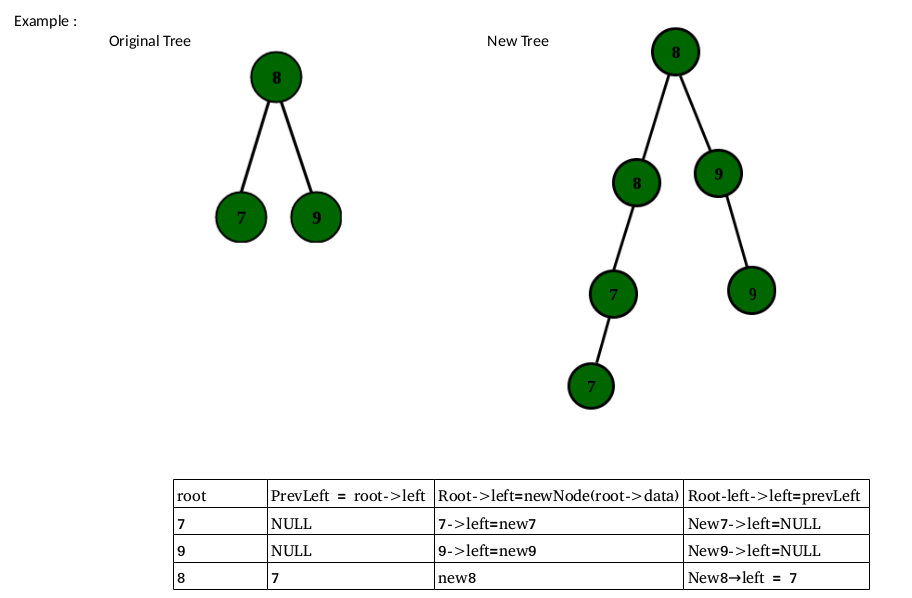
Option (B) is correct.
Que – 5. The function eraseDup() takes as input a linked list sorted in ascending order. It removes duplicate nodes from the list by traversing it just once. Choose the set of statements which replace X, Y, Z in given function.
void eraseDup(struct node* root) {
struct node* current = root;
if (X)
return;
while (current->next!=NULL) {
if (Y) {
struct node* nextOfNext = current->next->next;
free(current->next);
current->next = nextOfNext;
}
else {
Z
}
}
}
(A)
X: current == NULL
Y: current = current->next
Z: current->data = current->next->data;
(B)
X: current == NULL
Y: current->data == current->next->data
Z: current = current->next;
(C)
X: current->next == NULL
Y: current->next->data == current->next->next->data
Z: current = current->next;
(D)
X: current->next == NULL
Y: current->data = current->next->data
Z: current = current->next;
Solution:
As the input linked list is already sorted, we move down the list while comparing nodes next to each other. When the data in adjacent nodes is same, we delete the second node. Note: The node after the next node needs to be stored before performing the delete operation.
Option (B) is correct.
Share your thoughts in the comments
Please Login to comment...