Class 9 RD Sharma Solutions – Chapter 8 Introduction to Lines and Angles- Exercise 8.4 | Set 1
Last Updated :
28 Apr, 2021
Question 1: In figure, AB, CD and ∠1 and ∠2 are in the ratio 3 : 2. Determine all angles from 1 to 8.

Solution:
Assume,
∠1 = 3x and ∠2 = 2x
From the following figure: ∠1 and ∠2 are a linear pair of angles
Thus,
∠1 + ∠2 = 180°
3x + 2x = 180°
5x = 180°
x =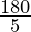
x = 36°
Hence,
∠1 = 3x = 108°
and
∠2 = 2x = 72°
We know that:
(Vertically opposite angles are equal)
Here the pairs of vertically opposite angles are:
(∠1 = ∠3);
(∠2 = ∠4);
(∠5, ∠7)
and
(∠6 = ∠8)
∠1 = ∠3 = 108°
∠2 = ∠4 = 72°
∠5 = ∠7
∠6 = ∠8
Now as it is known
(if a transversal intersects any parallel lines, then the corresponding angles are equal)
∠1 = ∠5 = ∠7 = 108°
∠2 = ∠6 = ∠8 = 72°
Hence,
∠1 = 108°, ∠2 = 72°, ∠3 = 108°, ∠4 = 72°, ∠5 = 108°, ∠6 = 72°, ∠7 = 108° and ∠8 = 72°
Question 2: In figure, I, m, and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠1, ∠2, and ∠3.

Solution:
Here as given in the figure
∠Y = 120° {Vertical opposite angles]}
∠3 + ∠Y = 180° {Linear pair angles}
∠3= 180 – 120
⇒ ∠3= 60°
As we can see the line ‘l’ is parallel to line ‘m’,
∠1 = ∠3 {Corresponding angles}
∠1 = 60°
Now, line ‘m’ is parallel to line ‘n’,
∠2 = ∠Y {Alternate interior angles}
∠2 = 120°
∠1 = 60°,
∠2 = 120°
and
∠3 = 60°.
Question 3: In figure, AB || CD || EF and GH || KL. Find ∠HKL.

Solution:
Construct: Extend LK to meet line GF at point P.
As shown below.

Here as from the figure,
CD || GF,
∠CHG =∠HGP = 60° {alternate angles}
∠HGP =∠KPF = 60° {Corresponding angles of parallel lines}
Thus,
∠KPG =180° – 60°
⇒∠KPG = 120°
∠GPK = ∠AKL= 120° {Corresponding angles of parallel lines}
∠AKH = ∠KHD = 25° {alternate angles of parallel lines}
Thus,
∠HKL = ∠AKH + ∠AKL
⇒25 + 120
⇒∠HKL = 145°
Question 4: In figure, show that AB || EF.

Solution:
Construct: Produce EF to intersect AC at point N.
As it is seen in the figure:

∠BAC = 57°
and
∠ACD = 22°+35° = 57°
{Alternative angles of parallel lines are equal}
BA || EF …..(i)
We know that,
Sum of Co-interior angles of parallel lines is 180°
EF || CD
∠DCE + ∠CEF = 35 + 145 = 180° …(ii)
From (i) and (ii)
AB || EF {Lines parallel to the same line are parallel to each other}
Hence Proved.
Question 5: In figure, if AB || CD and CD || EF, find ∠ACE.

Solution:
Given:
CD || EF
∠ FEC + ∠ECD = 180° {Sum of co-interior angles is supplementary to each other}
∠ECD = 180° – 130° = 50°
Now, BA || CD
∠BAC = ∠ACD = 70° {Alternative angles of parallel lines are equal}
Thus,
∠ACE + ∠ECD =70°
∠ACE = 70° – 50°
∠ACE = 20°
Question 6: In figure, PQ || AB and PR || BC. If ∠QPR = 102°, determine ∠ABC. Give reasons.

Solution:
Construct:
Extend line AB to meet line PR at point G.
As shown below;

Given:
PQ || AB,
∠QPR = ∠BGR =102° {Corresponding angles of parallel lines}
And
PR || BC,
∠RGB+ ∠CBG =180° {Corresponding angles are supplementary}
∠CBG = 180° – 102° = 78°
Thus,
∠CBG = ∠ABC
⇒ ∠ABC = 78°
Question 7: In figure, state which lines are parallel and why?

Solution:
As we know that,
If a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel
As we can see from the figure:
⇒ ∠EDC = ∠DCA = 100°
Lines DE and AC are intersected by a transversal DC such that the pair of alternate angles are equal.
Hence,
DE || AC
Question 8: In figure, if l||m, n || p and ∠1 = 85°, find ∠2.

Solution:
Given:
∠1 = 85°
We know that,
When a line cuts the parallel lines, the pair of alternate interior angles are equal.
⇒ ∠1 = ∠3 = 85°
Thus again, co-interior angles are supplementary,
Therefore
∠2 + ∠3 = 180°
∠2 + 55° =180°
∠2 = 180° – 85°
∠2 = 95°
Question 9: If two straight lines are perpendicular to the same line, prove that they are parallel to each other.
Solution:
Assume lines ‘l’ and ‘m’ are perpendicular to ‘n’,

Thus
∠1= ∠2=90°
Therefore,
The lines ‘l’ and ‘m’ are cut by a transversal line i.e. ‘n’
The corresponding angles are equal, so it can be seen that,
Line ‘l’ is parallel to line ‘m’.
Question 10: Prove that if the two arms of an angle are perpendicular to the two arms of another angle, then the angles are either equal or supplementary.
Solution:
Consider the angles be ∠ACB and ∠ABD
Let AC perpendicular to AB, and
CD is perpendicular to BD.
To Prove:
∠ACD = ∠ABD
∠ACD + ∠ABD =180°
Proof :
In a quadrilateral,
∠A+ ∠C+ ∠D+ ∠B = 360° {Sum of angles of quadrilateral is 360°}
180° + ∠C + ∠B = 360°
∠C + ∠B = 360° –180°
Thus,
∠ACD + ∠ABD = 180°
And
∠ABD = ∠ACD = 90°
Therefore, angles are equal as well as supplementary.
Share your thoughts in the comments
Please Login to comment...