Class 9 RD Sharma Solutions – Chapter 8 Introduction to Lines and Angles- Exercise 8.4 | Set 2

Question 11. In the given figure, lines AB and CD are parallel and P is any point as shown in the figure. Show that ∠ABP+ ∠CDP= ∠DPB.

Solution:

Here in the given figure:

Given:

AB || CD

Now draw a line XY passing through point P and parallel to AB and CD.

Here,XY || CD, thus, ∠CDP and ∠1are alternate interior opposite angles. Therefore,

∠1 = ∠CDP ……(i)

Similarly, we have XY || AB, thus, ∠ABP and∠2are alternate interior opposite angles. Therefore,

∠2 = ∠ABP ….(ii)

On adding (i) and (ii)

∠1 + ∠2 = ∠CDP + ∠ABP

∠DPB = ∠CDP + ∠ABP

Thus proved.

Question 12. In the given figure, AB||CD and P is any point shown in the figure. Prove that:

∠ABP+ ∠BPD+ ∠CDP= 360°

Solution:

The given figure is as follows:

It is given that AB || CD

Let us draw a line XY passing through point P and parallel to AB and CD.

We have XY || CD, thus, ∠CDP and∠2are consecutive interior angles. Therefore,

∠2 + ∠CDP = 180° ……(i)

Similarly, we have XY || AB, thus,∠CDP and∠2 are consecutive interior angles. Therefore,

∠1 + ∠ABP = 180° ……(ii)

On adding equation (i) and (ii), we get:

∠2 + ∠CDP + ∠1 + ∠ABP = 180° + 180°

(∠2 + ∠1) + ∠CDP + ∠ABP = 360°

∠ABP + ∠BPD + ∠CDP = 360°

Hence proved.

Question 13. Two unequal angles of a parallelogram are in the ratio 2 : 3. Find all its angles in degrees.

Solution:

The parallelogram can be drawn as follows:

It is given that

∠A : ∠C = 2 : 3

Therefore, let:

∠A = 2x and ∠C = 3x

We know that opposite angles of a parallelogram are equal.

Therefore,

∠A = ∠D

∠D = 2x

Similarly

∠B = 3x

Also, if AB || CD, then sum of consecutive interior angles is equal to180°. .

Therefore,

∠A + ∠C = 180°

2x + 3x = 180°

5x = 180°

x =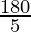

x = 36°

We have

∠A = 2x

∠A = 2(36°)

∠A = 72°

Also,

∠C = 3x

∠C = 3(36°)

∠C = 108°

Similarly,

∠D = 72°

And

∠B = 108°

Hence, the four angles of the parallelogram are as follows:

∠A = 72°, ∠B = 108°, ∠C = 72° and ∠D = 108°

Question 14. In each of the two lines is perpendicular to the same line, what kind of lines are they to each other?

Solution:

The figure can be drawn as follows:

Here, l ⊥ n and m ⊥n.

We need to find the relation between lines l and m

It is given that l ⊥n, therefore,

∠1 = 90° …….(i)

Similarly, we have m ⊥n, therefore,

∠2 = 90° …….(ii)

From (i) and (ii), we get:

∠1 = ∠2

But these are the pair of corresponding angles.

Theorem states: If a transversal intersects two lines in such a way that a pair of corresponding angles is equal, then the two lines are parallel.

Thus, we can say that l || m

Hence, the lines are parallel to each other.

Question 15. In the given figure, ∠1 = 60° and ∠2 =(23)rd23rdof a right angle. Prove that l||m.

Solution:

The figure is given as follows:

It is given that ∠1 = 60°

Also,

∠2 =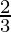(90°)

∠2 = 2(30°)

∠2 = 60°

Thus, we have ∠1 = ∠2

But these are the pair of corresponding angles.

Thus, l || m

Hence, proved.

Question 16. In the given figure, if l||m||n and ∠1 = 60°, find ∠2.

Solution:

The given figure is as follows:

We have l || m || n and ∠60°

Thus, we get ∠1 and ∠3 as corresponding angles.

Therefore,

∠3 = ∠1

∠3 = 60° ……….(i)

We have ∠3 and ∠4 forming a linear pair.

Therefore, they must be supplementary. That is;

∠3 + ∠4 = 180°

From equation (i)

60° + ∠4 = 180°

∠4 = 180° – 60°

∠4 = 120° ……(ii)

We have m || n

Thus, we get ∠2 and ∠4 as alternate interior opposite angles.

Therefore, these must be equal. That is,

∠2 = ∠4

From equation (ii), we get :

∠2 = 120°

Hence, the required value for ∠2 is 120°

Question 17. Prove that the straight lines perpendicular to the same straight line are parallel to one another.

Solution:

The figure can be drawn as follows:

Here, l ⊥ m and m ⊥ n.

We need to prove that l || m

It is given that l ⊥n, therefore,

∠1 = 90° …..(i)

Similarly, we have m ⊥ n, therefore,

∠2 = 90° ……(ii)

From (i) and (ii), we get

∠1 = ∠2

But these are the pair of corresponding angles.

Theorem states: If a transversal intersects two lines in such a way that a pair of corresponding angles is equal, then the two lines are parallel.

Thus, we can say that l || m.

Question 18. The opposite sides of a quadrilateral are parallel. If one angle of the quadrilateral is 60°, find the other angles.

Solution:

The quadrilateral can be drawn as follows:

Here, we have AB || CD and AC || BD.

Also, ∠ACD = 60°.

Thus, AB || CD.

Thus, ∠ACD and ∠BAC are consecutive interior angles.

Therefore, these two must be supplementary. i.e.

∠ACD + ∠BAC = 180°

60° + ∠BAC = 180°

∠BAC = 180° – 60°

∠BAC = 120°

Similarly, AC || BD .

Hence, ∠ACD and ∠CDB are consecutive interior angles.

Therefore, these two must be supplementary. i.e.

∠ACD + ∠CDB = 180°

60° + ∠CDB = 180°

∠CDB = 180° + 60°

∠CDB = 120°

Similarly, AB || CD.Thus, ∠ABD and ∠CDB are consecutive interior angles.

Therefore, these two must be supplementary. i.e.

∠ABD + ∠CDB = 180°

∠ABD + 120° = 180°

∠ABD = 180° – 120°

∠ABD = 60°

Thus, the other angles are as follows:

∠BAC = 120°

∠CDB = 120°

∠ABD = 60°

Question 19. Two lines AB and CD intersect at O. If ∠AOC+ ∠COB+ ∠BOD= 270°, find the measures of ∠AOC, ∠COB, ∠BOD and ∠DOA.

Solution:

Since, lines AB and CD intersect each other at point O.

Thus, ∠AOC and ∠BOD are vertically opposite angles.

Therefore,

∠AOC = ∠BOD …… (i)

Similarly,

∠COB = ∠AOD …… (ii)

Also, we have ∠AOC, ∠BOD, and ∠AOD forming a complete angle.

Therefore, ∠AOC + ∠BOD + ∠COB + ∠AOD = 360°

Given:

∠AOC + ∠COB + ∠BOD = 270°

Hence, we get

(∠AOC + ∠BOD + ∠COB) + ∠AOD = 360°

270° + ∠AOD = 360°

∠AOD = 360° – 270°

∠AOD = 90°

From (ii), we will get;

∠COB = 90°

As we know that ∠AOC and ∠COB form a linear pair. Therefore, these must be supplementary.

∠AOC + ∠COB = 180°

∠AOC + 90° = 180°

∠AOC = 180° – 90°

∠AOC = 90°

From (i), we get;

∠BOD = 90°

Question 20. In the given figure, p is a transversal to lines m and n, ∠2 = 120° and ∠5 = 60°. Prove that m||n.

Solution:

The given figure is;

Here we have that p is a transversal to lines m and n.

Also,

∠2 = 120° and ∠5 = 60°.

To prove: m || n

Here we have ∠2 = 120°.

Also, ∠2 and ∠4 are vertically opposite angles, therefore, these two must be equal. i.e.

∠4 = 120° ……(i)

Also, ∠5 = 60°

Adding this equation to (i), we will get :

∠4 + ∠5 = 120° + 60°

∠4 + ∠5 = 60°

But these are the consecutive interior angles.

Theorem states: If a transversal intersects two lines in such a way that a pair of consecutive interior angles is supplementary, then the two lines are parallel.

Thus, m || n.

Therefore, the lines are parallel to each other.