Class 9 RD Sharma Solutions – Chapter 8 Introduction to Lines and Angles- Exercise 8.2 | Set 2
Last Updated :
04 Nov, 2022
Question 11. In Figure, ACB is a line such that ∠DCA = 5x and ∠DCB = 4x. Find the value of x.

Solution:
It is given that ACB is a line in the figure given below.
Thus, ∠ACD and ∠BCD form a linear pair.
Therefore, their sum must be equal to 180°.
Or we can say that
∠ACD + ∠BCD = 180°
Also, ∠ACD = 4x and ∠BCD = 5x.
This further simplifies to:
4x + 5x = 180
9x = 180
x = 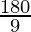
x = 20°
Question 12. In the given figure, ∠POR = 3x and ∠QOR = 2x + 10, find the value of x for which POQ will be a line.

Solution:
Here we have POQ as a line
So, ∠POR and ∠QOR form a linear pair.
Therefore, their sum must be equal to 180°
Or
∠POR + ∠QOR = 180°
It is given that ∠POR = (3x)° and ∠QOR = (2x + 10)°. On substituting these values above we get,
3x + (2x + 10) = 180°
3x + 2x + 10 = 180°
5x + 10 = 180°
5x = 180 – 10
5x = 170
x = 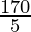
x = 34°
Question 13. In the given figure, a is greater than b by one-third of a right-angle. Find the values of a and b.

Solution:
It is given that in the figure given below; a is greater than b by one-third of a right angle.
Or we can say that, the difference between a and b is 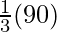
i.e.
a – b = 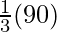
a – b = 30° ……..(i)
Also a and b form a linear pair. Therefore, their sum must be equal to 180°.
We can say that:
a + b = 180° ……….(ii)
On adding (i) and (ii), we get:
2a = 180 + 30
2a = 210
a = 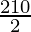
a = 105°
On putting a = 105 in (i)
105 – b = 30
-b = 30 – 105
-b = -75
b = 75°
Hence, a = 105° and b = 75°
Question 14. What value of y would make AOB a line in the given figure, if ∠AOC = 4y and ∠BOC = (6y + 30)

Solution:
Let us assume, AOB as a straight line.
This makes ∠AOC and ∠BOC to form a linear pair. Therefore, their sum must be equal to 180°.
We can say that:
∠AOC + ∠BOC = 180°
Also, ∠AOC = 4y and ∠BOC = 6y + 30. This further simplifies to:
4y + (6y + 30) = 180
10y + 30 = 180
10y = 180 – 30
10y = 150
y = 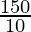
y = 15°
Thus, the value of y = 15° make AOB as a line.
Question 15. If the given figure, ∠AOF and ∠FOG form a linear pair.
∠EOB = ∠FOC = 90° and ∠DOC = ∠FOG = ∠AOB = 30°

(i) Find the measure of ∠FOE, ∠COB and ∠DOE.
(ii) Name all the right angles.
(iii) Name three pairs of adjacent complementary angles.
(iv) Name three pairs of adjacent supplementary angles.
(v) Name three pairs of adjacent angles.
Solution:
The given figure is as follows:
(i) It is given that ∠AOB, ∠FOE, ∠EOB and ∠FOG form a linear pair.
Therefore, their sum must be equal to 180°
i.e.
∠AOB + ∠FOE + ∠EOB + ∠FOG = 180°
It is given that:
∠FOG = 30°
∠AOB = 30°
∠EOB = 90° in equation above, we get:
∠AOB + ∠FOE + ∠EOB + ∠FOG = 180°
30° + ∠FOE + 90° + 30° = 180°
∠FOE + 150° = 180°
∠FOE = 180° – 150°
∠FOE = 30°
It is given that
∠FOC = 90°
From the above figure:
∠FOE + ∠DOE + ∠COD = 90°
30° + ∠DOE + 30° = 90°
∠DOE + 60° = 90°
∠DOE = 90° – 60°
∠DOE = 30°
Similarly, we have:
∠EOB = 90°
From the above figure:
∠DOE + ∠DOC + ∠COB = 90°
30° + 30° + ∠COB = 90°
∠COB + 60° = 90°
∠COB = 90° – 60°
∠COB = 30°
(ii) We have:
∠FOG = 30°
∠FOE = 30°
∠EOD = 30°
∠COD = 30°
∠COB = 30°
∠AOB = 30°
From the figure above and the measurements of the calculated angles we get two right angles as ∠DOG and ∠AOD.
Two right angles are already given as ∠FOC and ∠EOB
(iii) We have to find the three pair of adjacent complementary angles.
We know that ∠EOB is a right angle.
Therefore,
∠EOC and ∠COB are complementary angles.
Similarly, ∠AOD is a right angle.
Therefore,
∠AOC and ∠COD are complementary angles.
(iv) We have to find the three pair of adjacent supplementary angles.
Since, ∠AOG is a straight line.
Therefore, following are the three linear pair, which are supplementary:
∠AOB and ∠BOG
∠AOC and ∠COG
∠AOD and ∠DOG
(v) We have to find pair of adjacent angles, which are as follows:
∠AOB and ∠BOC
∠COD and ∠DOE
∠EOF and ∠FOG
Question 16. In the given figure, OP, OQ , OR, and OS are four rays. Prove that:
∠POQ + ∠QOR + ∠SOR + ∠POS = 360°.

Solution:
Let us draw TOP as a straight line.

Since, TOP is a line, therefore, ∠POQ, ∠QOR and ∠ROT form a linear pair.
Also, ∠POS and ∠SOT form a linear pair.
Thus, we have:
∠POQ + ∠QOR + ∠ROT = 180° ……(i)
and
∠POS + ∠SOT = 180° …….(ii)
On adding (i) and (ii), we get;
(∠POQ + ∠QOR + ∠ROT) + (∠POS + ∠SOT) = 180° + 180°
∠POQ + ∠QOR + (∠ROT + ∠SOT) + ∠POS = 360°
∠POQ + ∠QOR + ∠SOR + ∠POS = 360°
Hence proved.
Question 17. In the given figure, ray OS stand on a line POQ, Ray OR and ray OT are angle bisectors of ∠POS and∠SOQ respectively. If ∠POS = x, find ∠ROT.

Solution:
In the figure given below, we have
Ray OR as the bisector of ∠POS
Therefore,
∠POR = ∠ROS
or,
∠POS = 2∠ROS ………..(i)
Similarly, ray OT as the bisector of ∠SOQ
Therefore,
∠TOQ = ∠TOS
or,
∠QOS = 2∠TOS ……….(ii)
Also, Ray OS stand on a line POQ. Therefore, ∠POS and ∠QOS form a linear pair.
Thus,
∠POS + ∠QOS = 180°
From (i) and (ii)
2∠ROS + 2∠TOS = 180°
2(∠ROS + ∠TOS) = 180°
∠ROS + ∠TOS = 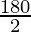
∠ROT = 90°
Question 18. In the given figure, lines PQ and RS intersect each other at point O. If ∠POR: ∠ROQ = 5:7, find all the angles.

Solution:
Let ∠POR and ∠ROQ be 5x and 7x respectively.
Since, Ray OR stand on line POQ. Thus, ∠POR and ∠ROQ form a linear pair.
Therefore, their sum must be equal to 180°.
Or,
∠POR + ∠ROQ = 180°
5x + 7x = 180°
12x = 180°
x = 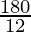
x = 15° …….(i)
Thus,
∠POR = 5x
= 5(15)
= 75
∠POR = 75°
Thus,
∠ROQ = 7x
= 7(15)
=105
∠ROQ = 105°
It is evident from the figure, that ∠QOS and ∠POR are vertically opposite angles.
And we know that vertically opposite angles are equal.
Therefore,
∠QOS = ∠POR
∠QOS = 75°
Similarly, ∠POS and ∠ROQ are vertically opposite angles.
And we know that vertically opposite angles are equal.
Therefore,
∠POS = ∠ROQ
∠POS = 105°
Question 19. In the given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that
∠ROS = 1212 (∠QOS − POS).

Solution:
The given figure shows:
We have POQ as a line. Ray OR is perpendicular to line PQ. Therefore,
∠ROQ = 90°
∠POR = 90°
From the figure above, we get
∠ROS + ∠POS = 90° ………(i)
∠POS and ∠QOS form a linear pair.
Therefore,
∠QOS + ∠POS = 180° ……(ii)
From (i) and (ii) equation we get:
∠QOS + ∠POS = 2 × 90 ∠QOS + ∠POS = 2 × 90
∠QOS + ∠POS = 2(∠ROS + ∠POS)
2∠ROS = ∠QOS – ∠POS
∠ROS = 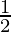 (∠QOS – ∠POS)
(∠QOS – ∠POS)
Hence, proved.
Share your thoughts in the comments
Please Login to comment...