Class 9 RD Sharma Solutions – Chapter 4 Algebraic Identities- Exercise 4.3 | Set 2
Last Updated :
22 Dec, 2022
Question 11. If 3x-2y=11 and xy = 12, find the value of 27x3-8y3
Solution:
Given, 3x-2y=11 and xy=12
we know that (a-b)3 = a3-b3-3ab(a-b)
(3x-2y)3 = 113
27x3-8y3-3(12)(11)=1331
27x3-8y3=1331+2376
27x3-8y3=3707
Hence, the value of 27x3-8y3 = 3707
Question 12. If (x4+1/x4)=119, Find the value of (x3-1/x3)
Solution:
Given, (x4+1/x4) =119 —— 1
we know that (x+y)2 = x2+y2+2xy
substitute the given value in eq-1
(x2+1/x2)2 = x4+1/x4+2(x2)(1/x2)
= x4+1/x4+2
= 119+2
= 121
(x2+1/x2)2 = ±11
Now, find (x-1/x)
we know that (x-y)2=x2+y2-2xy
(x-1/x)2 = x2+1/x2-2*x*1/x
= x2+1/x2 -2
= 11 -2
= 9
(x-1/x) = ±3
we need to find x3-1/x3
we know that , a3-b3=(a-b)(a2+b2-ab)
x3-(1/x)3=(x-1/x)(x2+(1/x)2-x*1/x)
Here, x2+1/x2 = 11 and x-1/x=3
x3-1/x3 = 3(11+1)
= 3(12)
= 36
Hence, the value of x3-1/x3=36
Question 13. Evaluate each of the following:
(a) (103)3
(b) (98)3
(c) (9.9)3
(d) (10.4)3
(e) (598)3
(f) (99)3
Solution:
Given:
(a) (103)3
we know that (a+b)3 = a3+b3+3ab(a+b)
(103)3 can be written as (100+3)3
Here, a=100 and b=3
(103)3 = (100+3)3
=1003+33+3(100)(3)(100+3)
=1000000+27+900(103)
=1092727
The value of (103)3=1092727
(b) (98)3
we know that (a-b)3 = a3-b3-3ab(a-b)
(98)3 = (100-2)3
= 1003-23-3(100)(2)(100-2)
= 1000000-8-600(98)
= 941192
The value of (98)3 = 941192
(c) (9.9)3
we know that (a-b)3 = a3-b3-3ab(a-b)
(10-0.1)3 = (10)3-(0.1)3-3(10)(0.1)(10-0.1)
= 1000 – 0.001-3(9.9)
= 970.299
The value of (9.9)3=970.299
(d) (10.4)3
we know that (a+b)3= a3+b3+3ab(a+b)
(10+0.4)3=(10)3+(0.4)3+3(10)(0.4)(10+0.4)
= 1000+0.064+12(10.4)
= 1124.864
The value of (10.4)3=1124.864
(e) (598)3
we know that (a-b)3 = a3-b3-3ab(a-b)
(600-2)3 = (600)3-23-3(600)(2)(600-2)
= 216000000 – 8 -(3600*598)
= 216000000 -8 – 2152800
= 213847192
The value of (598)3 = 213847192
(f) (99)3
we know that (a-b)3 = a3-b3-3ab(a-b)
(100-1)3 = (100)3 -13 -3(100)(1)(100-1)
= 1000000 – 1 -300*99
= 1000000 – 1 -29700
= 970299
The value of (99)3 = 970299
Question 14. Evaluate each of the following
(a) 1113 – 893
(b) 463 +343
(c) 1043+963
(d) 933 – 1073
Solution:
Given:
(a) 1113 – 893
The above equation can be written as (100+11)3 – (100-11)3
we know that , (a+b)3 -(a-b)3= 2[b3+3a2b]
Here, a=100 b=11
(100+11)3 – (100-11)3 = 2[113+3(100)2(11)]
= 2[1331 + 330000]
= 2[331331]
= 662662
The value of 1113-893 = 662662
(b) 463 + 343
The above equation can be written as (40+6)3 – (40-6)3
we know that , (a+b)3 +(a-b)3= 2[a3+3ab2]
Here, a = 40 and b=6
(40+6)3 – (40-6)3 = 2[(40)3+3(6)2(40)]
= 2[64000+3*36*40]
=2[68320]
= 136640
The value of 463 +343=136640
(c) 1043 +963
The above equation can be written as (100+4)3 + (100-4)3
we know that, (a+b)3 +(a-b)3= 2[a3+3ab2]
here, a = 100 , b= 4
(100+4)3 +(100-4)3 = 2[(100)3 +3(100)(4)2]
= 2[1000000 + 300*16]
= 2[1004800]
= 2009600
The value of 1043 + 963 = 2009600
(d) 933 – 1073
The above equation can be written as (100-7)3 – (100+7)3
we know that, (a-b)3 -(a+b)3= -2[b3+3a2b]
here, a = 100 , b= 7
(100-7)3 – (100+7)3 = -2[73+3*(100)2*7]
= -2[210343]
= -420686
The value of 933 – 1073 = -420686
Question 15. If x+1/x = 3, calculate x2+1/x2, x3+1/x3, x4+1/x4
Solution:
Given, x+1/x=3
we know that (x+y)2= x2+y2+2xy
(x+1/x)2= x2+(1/x)2+2x(1/x)
(3)2 = x2+(1/x)2 +2
x2+1/x2 =7
squaring on both the sides,
(x2+1/x2)2 = 49
x4+1/x4+2(x2)(1/x2) = 49
x4 +1/x4 = 49-2
x4+1/x4 = 47
again cubing on both the sides,
(x+1/x)3 = x3+1/x3+3*x*1/x(x+1/x)
33 = x3+1/x3+3(3)
x3+1/x3=27-9
x3+1/x3 = 18
The value x2+1/x2 =7, x3+1/x3 = 18, x4+1/x4 = 47
Question 16. If x4+1/x4=194, calculate x2+1/x2, x3+1/x3, x+1/x
Solution:
Given,
x4+1/x4=194 —– 1
add and subtract (2*x2*1/x2) on the left side in above given equation
x4+1/x4 +2*x2*1/x2 -2*x*1/x2 = 194
x4+1/x4+2*x2*1/x2 -2 =194
(x2)2+(1/x2)2+ 2*x2*1/x2 = 196
(x2+1/x2)2 = 196
(x2+1/x2) = 14 ——— 2
add and subtract (2*x*1/x) on the left side in above given equation
x2+1/x2+2*x*1/x-2*x*1/x =14
(x+1/x)2 = 14 +2
(x+1/x) = 4 ———— 3
Now cubing eq-3 on both sides.
(x+1/x)3 = 43
x3+1/x3+3*x*1/x(x+1/x) = 64
x3+1/x3 +3*4 = 64
x3+1/x3 = 64 -12
= 52
Hence, the values of (x2+1/x2) = 14, (x3+1/x3) = 52, (x+1/x) = 4
Question 17. Find the value of 27x3+8y3, if
(a) 3x+2y=14 and xy = 8
(b) 3x+2y = 20 and xy=14/9
Solution:
(a) Given, 3x+2y = 14 and xy = 8
cubing on both the sides
(3x+2y)3 = 143
we know that, (a+b)3=a3+b3+3ab(a+b)
27x3+8y3+3(3x)(2y)(3x+2y) = 2744
27x3+8y3+18xy(3x+2y) = 2744
27x3+8y3+18*8*14 = 2744
27x3+8y3 = 2744 – 2016
27x3 +8y3 = 728
Hence, the value of 27x3 +8y3 = 728
(b) Given, 3x+2y = 20 and xy=14/9
cubing on both the sides
we know that, (a+b)3=a3+b3+3ab(a+b)
27x3+8y3+3(3x)(2y)(3x+2y) = 8000
27x3+8y3+18xy(3x+2y) = 8000
27x3+8y3+18*14/9*20 = 8000
27x3+8y3 = 8000 – 560
= 7440
Hence, the value of 27x3+8y3 = 7440
Question 18. Find the value of 64x3-125z3, if 4x-5z=16 and xz=12
Solution:
Given, 64x3 – 125z3
Here, 4x -5z = 16 and xz = 12
cubing (4x-5z)3 = 163
we know that (a-b)3 =a3-b3-3ab(a-b)
(4x -5z)3 = (4x)3-(5z)3-3(4x)(5z)(4x-5z)
(16)3 = 64x3 -125z3-60(4x-5z)
4096 = 64x3-125z3-60(16)
64x3-125z3 = 4096 + 960
= 5056
Hence, the value of 64x3 – 125z3 = 5056
Question 19. If x-1/x =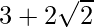 , find the value of x3-1/x3
, find the value of x3-1/x3
Solution:
Given, x-1/x =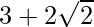
cubing both the sides,
we know that , (a-b)3 = a3-b3-3ab(a-b)
(x-1/x)3 = x3 -1/x3 -3*x*1/x(x-1/x)
(3+2\sqrt{2})^3 = x3-1/x3 -3(3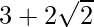 )
)
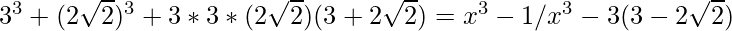
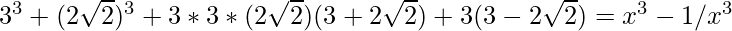
x3-1/x3 = 108+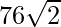
Hence, the value of x3-1/x3 = 108+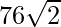
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...