Class 9 RD Sharma Solutions – Chapter 3 Rationalisation- Exercise 3.2 | Set 1
Last Updated :
06 Feb, 2023
Question 1. Rationalise the denominator of each of the following (i-vii):
(i)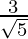
(ii)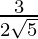
(iii)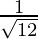
(iv)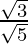
(v)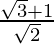
(vi)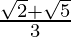
(vii)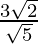
Solution:
(i) We know that rationalisation factor for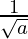 is
is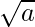 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression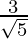 by
by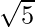 . to
. to
get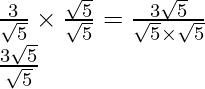
Hence, the given expression is simplified to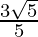 .
.
(ii) We know that rationalisation factor for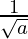 is
is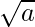 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression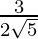 by
by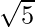 . to
. to
get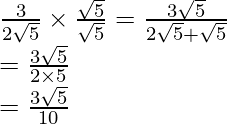
Hence, the given expression is simplified to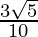
(iii) We know that rationalisation factor for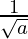 is
is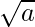 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression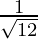 by
by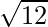 .
.
to get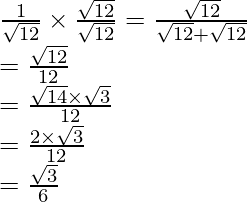
Hence the given expression is simplified to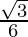
(iv) We know that rationalisation factor for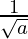 is
is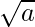 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression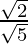 is
is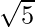 .
.
to get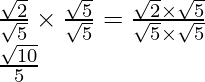
Hence, the given expression is simplified to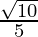
(v) We know that rationalisation factor for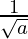 is
is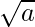 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression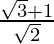 by
by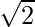 to get
to get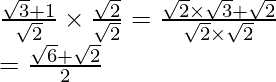
Hence, the given expression is simplified to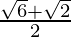
(vi) We know that rationalisation factor for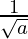 is
is 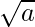 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression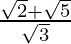 by
by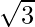 to get
to get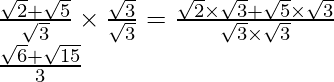
Hence, the given expression is simplified to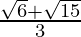 .
.
(vii) We know that rationalisation factor for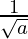 is
is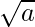 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression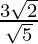 by
by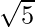 to get
to get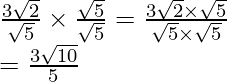
Hence, the given expression is simplified to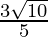
Question 2. Find the value to three places of decimals of each of the following. It is given that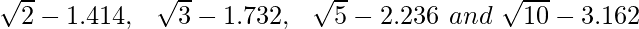
(i)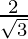
(ii)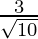
(iii)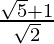
(iv)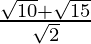
(v)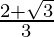
(vi)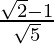
Solution:
(i) We know that rationalisation factor of the denominator is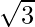 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression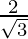 by
by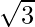 to get
to get
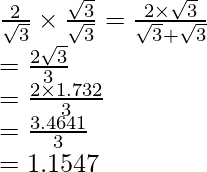
The value of expression 1.1547 can be round off to decimal places as 1.155.
Hence, the given expression is simplified to 1.155.
(ii) We know that rationalisation factor of the denominator is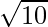 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression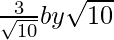
to get
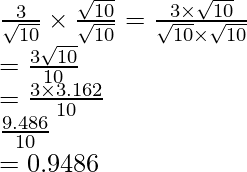
The value of expression 0.9486 can be round off to decimal places as 0.949.
Hence, the given expression is simplified to 0.949.
(iii) We know that rationalisation factor of the denominator is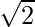 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression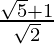 by
by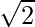
to get
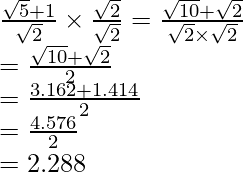
The value of expression 2.288 can be round off to decimal places as 2.288.
Hence, the given expression is simplified to 2.288.
(iv) We know that rationalisation factor of the denominator is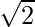 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression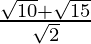
by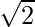 to get
to get
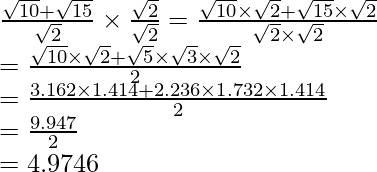
The value of expression 4.9746 can be round off to decimal places as 4.975.
Hence, the given expression is simplified to 4.975.
(v) We know that rationalisation factor of the denominator is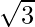 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression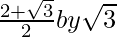 to get
to get
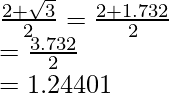
The value of expression 1.24401 can be round off to decimal places as 1.244.
Hence, the given expression is simplified to 1.244.
(vi) We know that rationalisation factor of the denominator is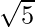 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression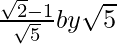
to get
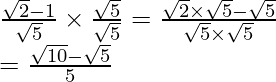
Putting the value of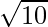 and
and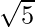 , we get
, we get
The value of expression 0.1852 can be round off to decimal places as 0.185.
Hence, the given expression is simplified to 0.185
Question 3. Express each one of the following with rational denominator:
(i)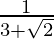
(ii)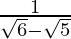
(iii)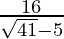
(iv)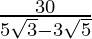
(v)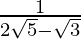
(vi)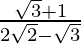
(vii)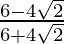
(viii)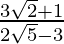
(ix)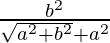
Solution:
(i) We know that rationalisation factor for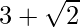 is
is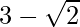 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression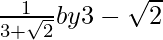 to get
to get
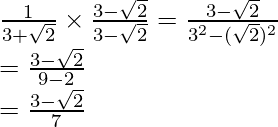
Hence, the given expression is simplified with rational denominator to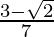
(ii) We know that rationalisation factor for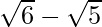 is
is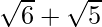 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression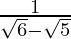 by
by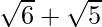
to get
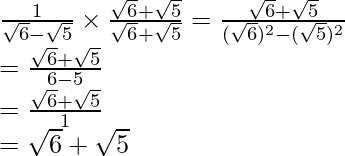
Hence, the given expression is simplified with rational denominator to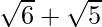
(iii) We know that rationalisation factor for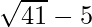 is
is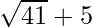 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression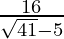 by
by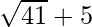
to get
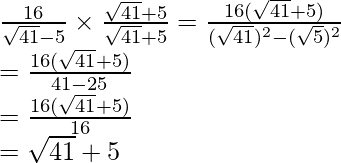
Hence, the given expression is simplified with rational denominator to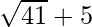
(iv) We know that rationalisation factor for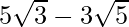 is
is 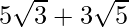 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression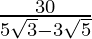 by
by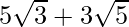
to get
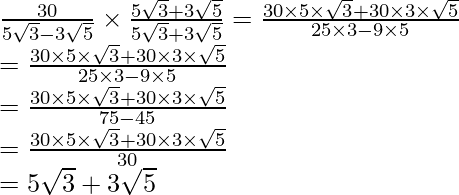
Hence, the given expression is simplified with rational denominator to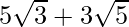
(v) We know that rationalisation factor for is . We will multiply numerator and denominator of the given expression by to get
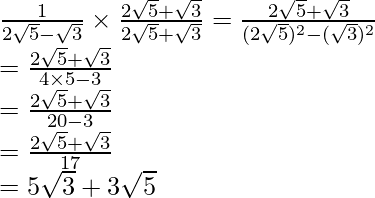
Hence, the given expression is simplified with rational denominator to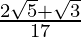
(vi) We know that rationalisation factor for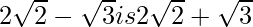 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression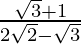 by
by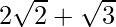 to get
to get
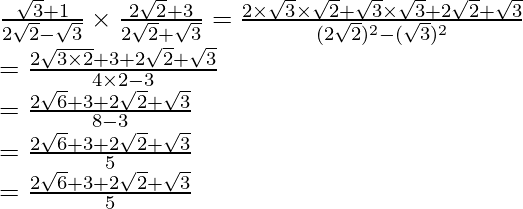
Hence, the given expression is simplified with rational denominator to=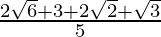
(vii) We know that rationalisation factor for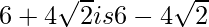 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression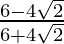 by
by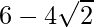 to get
to get
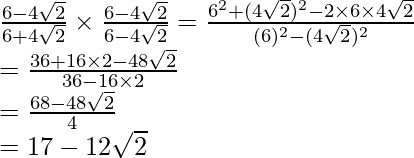
Hence, the given expression is simplified with rational denominator to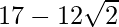
(viii) We know that rationalisation factor for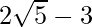 is
is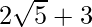 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression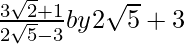 to get
to get
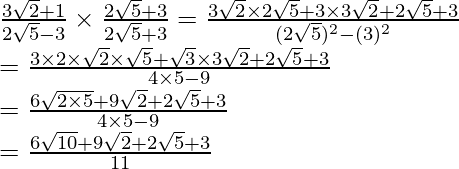
Hence, the given expression is simplified with rational denominator to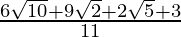
(ix) We know that rationalisation factor for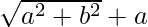 is
is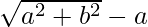 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression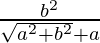 by
by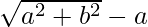 to get
to get
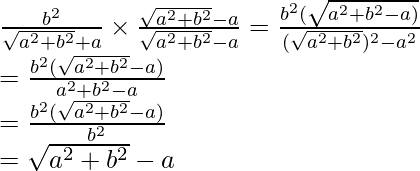
Hence, the given expression is simplified with rational denominator to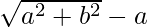
Question 4. Rationales the denominator and simplify:
(i)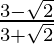
(ii)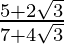
(iii)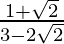
(iv)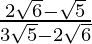
(v)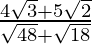
(vi)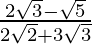
Solution:
(i) We know that rationalisation factor for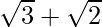 is
is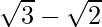 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression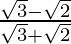 by
by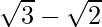 to get
to get
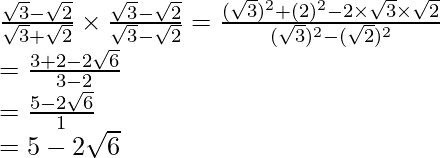
Hence, the given expression is simplified to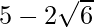 .
.
(ii) We know that rationalisation factor for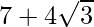 is
is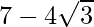 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression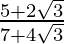 by
by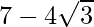 to get
to get
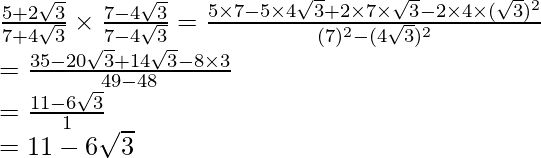
Hence, the given expression is simplified to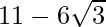 .
.
(iii) We know that rationalisation factor for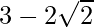 is
is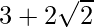 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression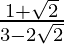 by
by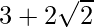 to get
to get
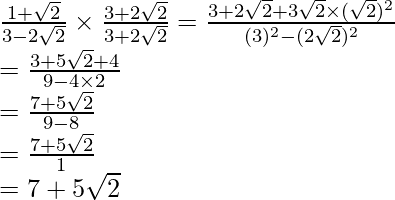
Hence, the given expression is simplified to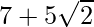 .
.
(iv) We know that rationalisation factor for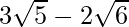 is
is 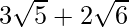 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression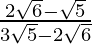 by
by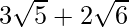 to get
to get
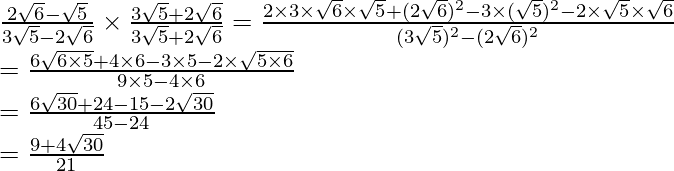
Hence, the given expression is simplified to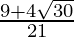 .
.
(v) We know that rationalisation factor for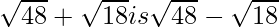 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression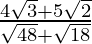 by
by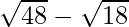 to get
to get
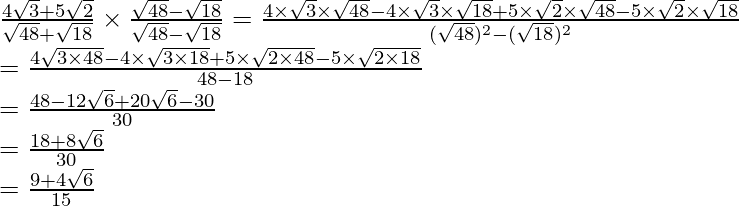
Hence, the given expression is simplified to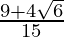 .
.
(vi) We know that rationalisation factor for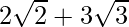 is
is 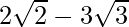 . We will multiply numerator and denominator of the given expression
. We will multiply numerator and denominator of the given expression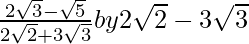 to get
to get
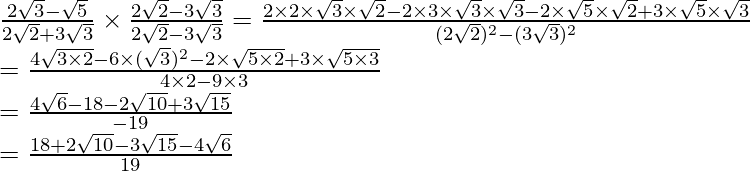
Hence, the given expression is simplified to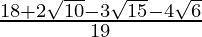 .
.
Question 5. Simplify:
(i)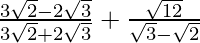
(ii)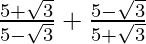
(iii)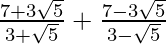
(iv)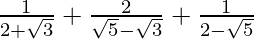
(v)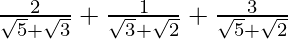
Solution:
(i) We know that rationalisation factor for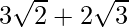 and
and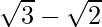 are
are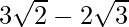 and
and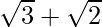 respectively.
respectively.
We will multiply numerator and denominator of the given expression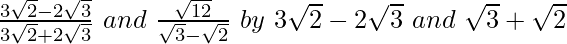 respectively, to get
respectively, to get
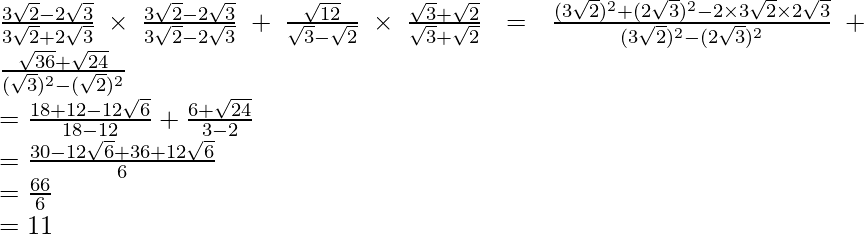
Hence, the given expression is simplified to 11.
(ii) We know that rationalisation factor for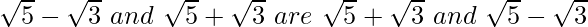 respectively.
respectively.
We will multiply numerator and denominator of the given expression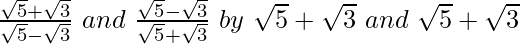 respectively, to get
respectively, to get
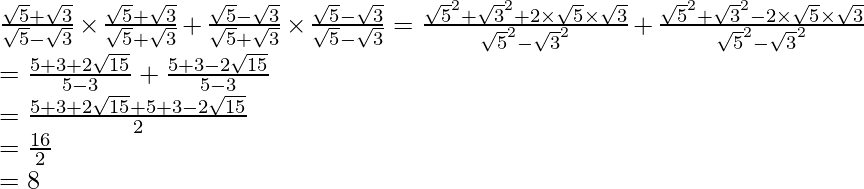
Hence, the given expression is simplified to 8.
(iii) We know that rationalisation factor for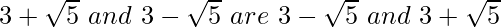 respectively.
respectively.
We will multiply numerator and denominator of the given expression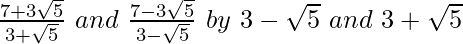 respectively, to get
respectively, to get
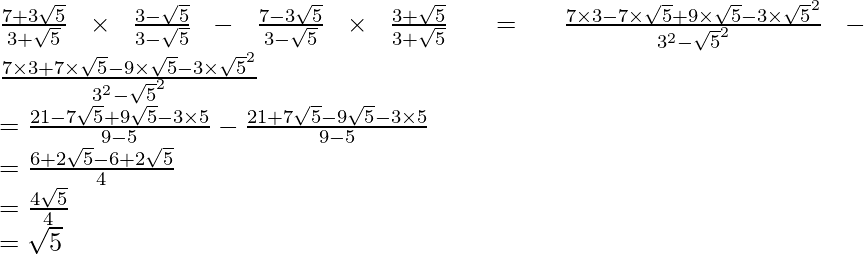
Hence, the given expression is simplified to 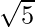 .
.
(iv) We know that rationalisation factor for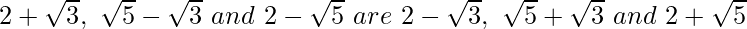 respectively.
respectively.
We will multiply numerator and denominator of the given expression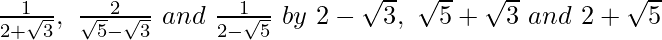 respectively, to get
respectively, to get
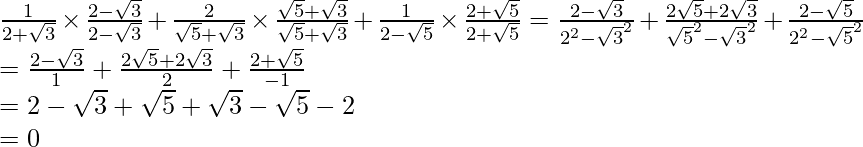
Hence, the given expression is simplified to 0 .
(v) We know that rationalisation factor for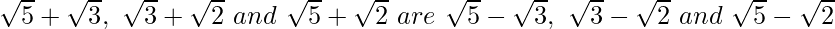 respectively.
respectively.
We will multiply numerator and denominator of the given expression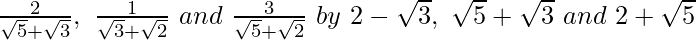 respectively, to get
respectively, to get
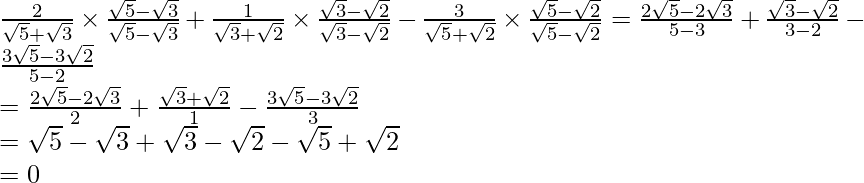
Hence, the given expression is simplified to 0.
Share your thoughts in the comments
Please Login to comment...