Class 9 RD Sharma Solutions – Chapter 14 Quadrilaterals – Exercise 14.2

Question 1. Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram.

Solution:

Given: Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°.

(3x – 2)°= (50 – x)° [Opposite sides of a parallelogram are equal]

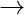3x + x = 50 + 2

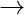4x = 52

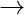x = 13

Angle x is 13°

(3x – 2) = (3*13 – 2) = 37°

(50 – x)° = (50 – 13)°= 37°

x + 37°= 180° [Adjacent angles of a parallelogram are supplementary]

x = 180°− 37°= 143°

Hence, required angles are : 37°, 143°, 37°, 143°.

Question 2. If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.

Solution:

Let the measure of the angle be x.

Therefore, the measure of the angle adjacent is 2x/3

Hence, x + 2x/3 = 180° [Consecutive angles of a parallelogram are supplementary]

2x + 3x = 540°

5x = 540°

x = 108°

Now,

⟹ x + 108°= 180° [Consecutive angles of a parallelogram are supplementary]

⟹ x + 108°= 180°

⟹ x = 180°- 108°= 72°

⟹ x = 72°

required angles are180°, 72°, 180°, 72°

Question 3. Find the measure of all the angles of a parallelogram, if one angle is 24°less than twice the smallest angle.

Solution:

x + 2x – 24°= 180° [Consecutive angles of a parallelogram are supplementary]

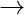3x – 24°= 180°

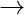3x = 108° + 24°

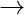3x = 204°

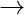x = 204/3 = 68°

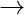x = 68°

Other angle of parallelogram=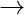2x – 24°= 2*68°- 24°= 112°

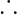required angles are 68°,112°,68°,112°

Question 4. The perimeter of a parallelogram is 22 cm. If the longer side measures 6.5 cm what is the measure of the shorter side?

Solution:

Given: perimeter of a parallelogram is 22 cm

Let us consider the shorter side be ‘y’.

perimeter = y + 6.5 + 6.5 + x [Sum of all sides]

22 = 2(y + 6.5)

11 = y + 6.5

y = 11 – 6.5 = 4.5 cm

Hence, the measure of the shorter side = 4.5 cm

Question 5. In a parallelogram ABCD, ∠D = 135°. Determine the measures of ∠A and ∠B.

Solution:

In a parallelogram ABCD

Given: ∠D=135°

So, ∠D + ∠C = 180° [Consecutive angles of a parallelogram are supplementary]

∠C = 180°− 135°

∠C = 45°

In a parallelogram opposite sides are equal.

∠A = ∠C = 45° [opposite sides of parallelogram are equal]

∠B = ∠D = 135°

hence, the measures of ∠A and ∠B are 45°,135°respectively.

Question 6. ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D.

Solution:

In a parallelogram ABCD

Given: ∠A = 70°

∠A + ∠B = 180° [Consecutive angles of a parallelogram are supplementary]

70°+ ∠B = 180° [given ∠A = 70°]

∠B = 180°− 70°

∠B = 110°

Now,

∠A = ∠C = 70° [opposite sides of parallelogram are equal]

∠B = ∠D = 110°

hence, the measures of ∠A and ∠B are 70°,110°respectively.

Question 7. In Figure, ABCD is a parallelogram in which ∠A = 60°. If the bisectors of ∠A, and ∠B meet at P, prove that AD = DP, PC = BC and DC = 2AD.

Solution:

Given: ∠A = 60°

To prove: AD = DP, PC = BC and DC = 2AD

AP bisects ∠A

so, ∠DAP = ∠PAB = 30°

Now,

∠A + ∠B = 180° [Consecutive angles of a parallelogram are supplementary]

∠B + 60°= 180°

∠B = 180°− 60°

∠B = 120°

BP bisects ∠B

so, ∠PBA = ∠PBC = 60°

∠PAB = ∠APD = 30°[Alternate interior angles]

Therefore, AD = DP [Sides opposite to equal angles are in equal length]

Similarly

∠PBA = ∠BPC = 60° [Alternate interior angles]

Therefore, PC = BC

DC = DP + PC

DC = AD + BC [ DP = AD and PC = BC ]

DC = 2AD [Since, AD = BC, The opposite sides of parallelogram are parallel and congruent]

hence proved.

Question 8. In figure, ABCD is a parallelogram in which ∠DAB = 75°and ∠DBC = 60°. Compute ∠CDB, and ∠ADB.

Solution:

Given: ∠DAB = 75°and ∠DBC = 60°

To find ∠CDB and ∠ADB

∠CBD = ∠ADB = 60° [Alternate interior angle. AD∥ BC and BD is the transversal]

InBDA

∠DAB + ∠ADB + ∠ABD = 180° [Angle sum property]

75°+ 60°+ ∠CDB = 180°

∠ABD = 180°− (135°)

∠ABD = 45°

∠ABD = ∠CDB = 45° [Alternate interior angle. AD∥ BC and BD is the transversal]

Hence, ∠CDB = 45°, ∠ADB = 60°

Question 9. In figure, ABCD is a parallelogram and E is the mid-point of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

Solution:

Given: ABCD is a parallelogram and E is the mid-point of side BC.

To prove: AF = 2AB.

Now,

In ΔBEF and ΔCED

∠BEF = ∠CED [Verified opposite angle]

BE = CE [Since, E is the mid-point of BC]

∠EBF = ∠ECD [Since, Alternate interior angles are equal]

ΔBEF ≅ ΔCED [ASA congruence]

BF = CD [Corresponding Parts of Congruent Triangle]

AF = AB + AF

AF = AB + CD [BF = CD by Corresponding Parts of Congruent Triangle ]

AF = AB + AB [CD=AB, The opposite sides of parallelogram are parallel and congruent]

AF = 2AB.

Hence proved.

Question 10. Which of the following statements are true (T) and which are false (F)?

(i) In a parallelogram, the diagonals are equal.

(ii) In a parallelogram, the diagonals bisect each other.

(iii) In a parallelogram, the diagonals intersect each other at right angles.

(iv) In any quadrilateral, if a pair of opposite sides is equal, it is a parallelogram.

(v) If all the angles of a quadrilateral are equal, it is a parallelogram.

(vi) If three sides of a quadrilateral are equal, it is a parallelogram.

(vii) If three angles of a quadrilateral are equal, it is a parallelogram.

(viii) If all the sides of a quadrilateral are equal, it is a parallelogram.

Solution:

(i) False

(ii) True

(iii) False

(iv) False

(v) True

(vi) False

(vii) False

(viii) True