Class 9 RD Sharma Solutions – Chapter 2 Exponents of Real Numbers- Exercise 2.1
Last Updated :
04 May, 2021
Question 1 (i). Simplify 3(a4b3)10 × 5(a2b2)3
Solution:
Given 3(a4b3)10 × 5(a2b2)3
= 3 × a40 × b30 × 5 × a6 × b6
= 3 × a46 × b36 × 5 [am × an = am+n]
= 15 × a46 × b36
= 15a46b36
Thus, 3(a4b3)10 × 5(a2b2)3 = 15a46b36
Question 1 (ii). Simplify (2x-2y3)3
Solution:
Given (2x-2y3)3
= 23 × x-6 × y9
= 8 × x-6 × y9 [am × an = am+n]
= 8x-6y9
Thus, (2x-2y3)3 = 8x-6y9
Question 1 (iii). Simplify 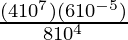
Solution:
Given 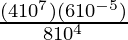
=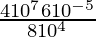
=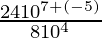 [am × an = am+n]
[am × an = am+n]
=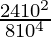
= 3/102
= 3/100
Thus, 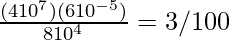
Question 1 (iv). Simplify 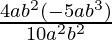
Solution:
Given 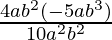
= 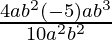
= 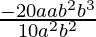
= 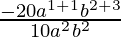 [am × an = am+n]
[am × an = am+n]
= -2×a2×b5×a-2×b-2
= -2×a2+(-2)×b5+(-2) [am × an = am+n]
= -2×a0×b3
= -2b3 [a0=1]
Thus, 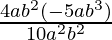 =-2b3
=-2b3
Question 1 (v). Simplify 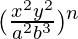
Solution:
Given 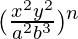
= 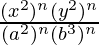
= 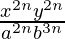 [am × an = am+n]
[am × an = am+n]
Thus, 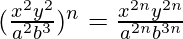
Question 1 (vi). Simplify 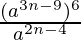
Solution:
Given 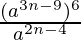
= 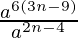 [(am)n = amn]
[(am)n = amn]
= 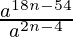
= a18n-54 × a-(2n-4) [am × an = am+n]
= a18n-54-2n+4
= a16n-50
Thus, 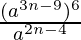 = a16n-50
= a16n-50
Question 2 (i) If a = 3 and b = -2,find the value of aa + bb
Solution:
Given a = 3 and b = -2
On substituting the value of a and b in aa + bb, we get
aa + bb = 33 + (-2)-2
= 27 + 1/4
= (108 + 1)/4
= 109/4
Thus, aa + bb = 109/4
Question 2 (ii). If a = 3 and b = -2,find the value of ab + ba
Solution:
Given a = 3 and b = -2
On substituting the value of a and b in ab + ba, we get
ab + ba = 3-2 + (-2)3
= 1/9 + (-8)
= (1 – 72)/9
= -71/9
Thus, ab + ba = -71/9
Question 2 (iii). If a = 3 and b = -2,find the value of (a + b)ab.
Solution:
Given a = 3 and b = -2
On substituting the value of a and b in (a + b)ab, we get
(a + b)ab = (3 + (-2))3×-2
= (1)-6
= 1
Thus, (a + b)ab = 1
Question 3 (i). Prove that 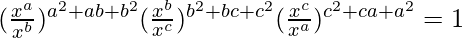
Solution:
Let us first solve left-hand side of the given equation
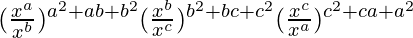
By using the formula (am)n = amn, we get
= 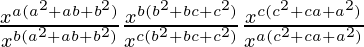
By using the formula am/an = am-n, we get
= 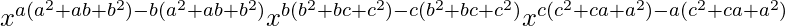
= 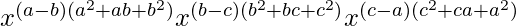
= 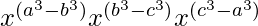
By using the formula am × an = am+n , we get
=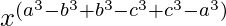
= x
= 1
= Right-hand side of the given equation
Thus, we proved that 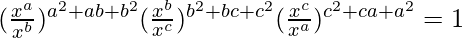
Question 3 (ii). Prove that 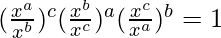
Solution:
Let us consider the left-hand side of the given equation
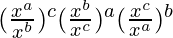
By using the formula, (am)n = amn, we get
= 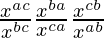
= 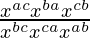
= 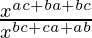 [am × an = am+n]
[am × an = am+n]
= 1
= Right-hand side of the given equation
Thus, we proved that 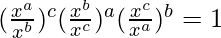
Question 3 (iii). Prove that 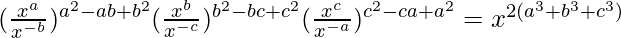
Solution:
Let us first solve left-hand side of the given equation
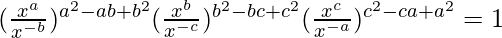
By using the formula (am)n = amn, we get
= 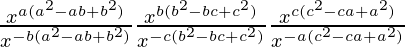
By using the formula am/an = am-n, we get
= 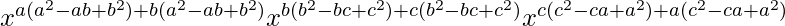
= 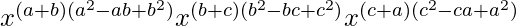
= 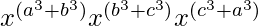
By using the formula am × an = am+n , we get
= 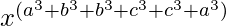
= 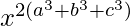
= Right-hand side of the given equation
Thus, we proved that 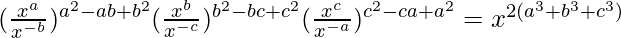
Question 4 (i). Prove that 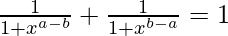
Solution:
Let us first consider the left-hand side of given equation
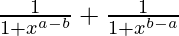
= 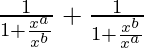
= 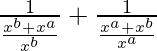
= 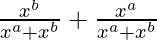
= 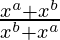
= 1
= Right-hand side of the given equation
Thus, we proved that 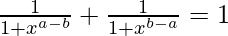
Question 4 (ii). Prove that 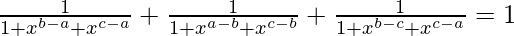
Solution:
Let us first consider the left-hand side of given equation
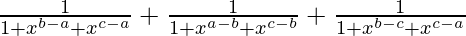
= 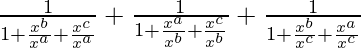
= 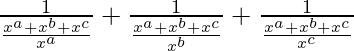
= 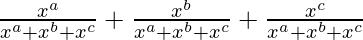
= 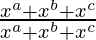
= 1
= Right-hand side of the given equation
Thus, we proved that 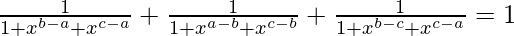
Question 5 (i). Prove that 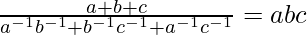
Solution:
Let us first consider the left-hand side of given equation
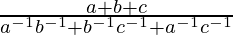
= 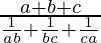
= 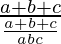
= abc
= Right hand side of the given equation
Thus, we proved that 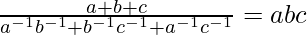
Question 5 (ii). Prove that 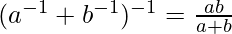
Solution:
Let us first consider the left hand side of given equation
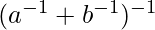
= 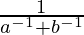
= 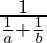
= 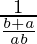
= 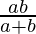
= Right hand side of the given equation
Thus, we proved that 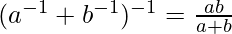
Question 6. If abc = 1, show that 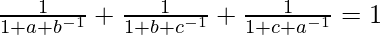
Solution:
Given abc = 1
⇒ c = 1/ab
Let us first consider the left-hand side of given equation
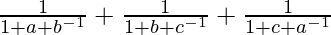
= 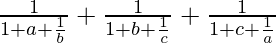
= 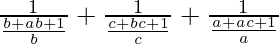
= 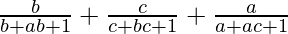
By substituting the value of c in above equation, we get
= 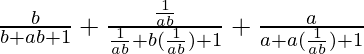
= 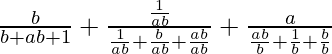
= 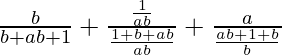
= 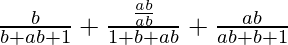
= 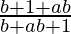
= 1
= Right hand side of the given equation
Thus, we have shown that if abc = 1, 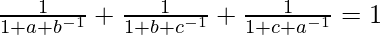
Question 7 (i). Simplify 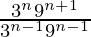
Solution:
Given 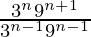
= 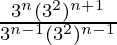
= 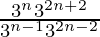
= 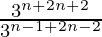 [am × an = am+n]
[am × an = am+n]
= 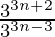
= 33n+2-(3n-3) [am/an = am-n]
= 35
= 243
Thus, 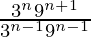 = 243
= 243
Question 7 (ii). Simplify 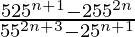
Solution:
Given 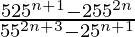
= 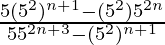
= 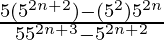
= 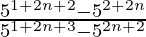 [am × an = am+n]
[am × an = am+n]
= 
= 4/24
= 1/6
Thus, 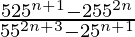 = 1/6
= 1/6
Question 7 (iii). Simplify 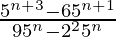
Solution:
Given, 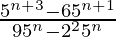
= 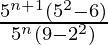
=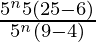
= (19 × 5)/5
= 19
Thus, 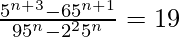
Question 7 (iv). Simplify 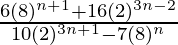
Solution:
Given 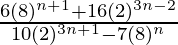
= 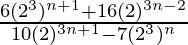
= 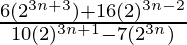
= 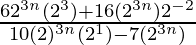
= 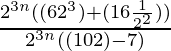
= 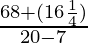
= (48 + 4)/13
= 52/13
= 4
Thus, 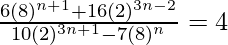
Question 8 (i). Solve the equation 72x+3 = 1 for x.
Solution:
Given equation 72x+3 = 1
We know that, for any a∈ Real numbers, a0 = 1
Let a = 7
⇒ 72x+3 = 70
Since the bases are equal, let us equate the exponents
⇒ 2x + 3 = 0
⇒ x = -3/2
Thus, the value of x is -3/2
Question 8 (ii). Solve the equation 2x+1 = 4x-3 for x.
Solution:
Given 2x+1 = 4x-3
We can write 4 = 22
⇒ 2x+1 = 22(x-3)
⇒ 2x+1 = 22x-6
Since the bases are equal, let us equate the exponents
⇒ x + 1 = 2x – 6
⇒ x = 7
Thus, the value of x is 7
Question 8 (iii). Solve the equation 25x+3 = 8x+3 for x.
Solution:
Given 25x+3 = 8x+3
We know that 8 = 23
⇒ 25x+3 = 23(x+3)
⇒ 25x+3 = 23x+9
Since the bases are equal, let us equate the exponents
⇒ 5x + 3 = 3x + 9
⇒ 5x – 3x = 9 – 3
⇒ 2x = 6
⇒ x = 3
Thus, the value of x is 3
Question 8 (iv). Solve the equation 42x = 1/32 for x.
Solution:
Given 42x = 1/32
⇒ 22(2x) = 1/32
⇒ 22(2x) × 32 = 1
⇒ 24x × 25 = 1
⇒ 24x+5 = 20
Since the bases are equal, let us equate the exponents
⇒ 4x + 5 = 0
⇒ x = -5/4
Thus, the value of x is -5/4
Question 8 (v). Solve the equation 4x – 1 × (0.5)3-2x = (1/8)x for x.
Solution:
Given 4x – 1 × (0.5)3-2x = (1/8)x
⇒ 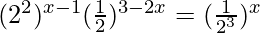
⇒ 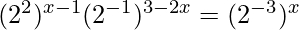
⇒ 22(x-1) × 2-(3-2x) = 2-3x
⇒ 22x-2-3+2x = 2-3x
⇒ 24x-5 = 2-3x
Since the bases are equal, let us equate the exponents
⇒ 4x – 5 = -3x
⇒ 7x = 5
⇒ x = 5/7
Thus, the value of x is 5/7
Question 8 (vi). Solve the equation 23x-7 = 256 for x.
Solution:
Given 23x-7 = 256
⇒ 23x-7 = 28
Since the bases are equal, let us equate the exponents
⇒ 3x – 7 = 8
⇒ x = 15/3
⇒ x = 5
Thus, the value of x is 5
Question 9 (i). Solve the equation 22x – 2x+3 + 24 = 0 for x.
Solution:
Given 22x – 2x+3 + 24 = 0
⇒ (2x)2 – 2 × 2x × 22 + (22)2 = 0
⇒ (2x – 22)2 = 0
⇒ 2x – 22 = 0
⇒ 2x = 22
Since the bases are equal, let us equate the exponents
⇒ x = 2
Thus, the value of x is 2
Question 9 (ii). Solve the equation 32x+4 + 1 = 2.3x+2 for x.
Solution:
Given 32x+4 + 1 = 2.3x+2
⇒ 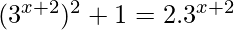
⇒ 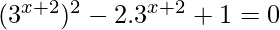
⇒ (3x+2 – 1)2 = 0
⇒ 3x+2 – 1 = 0
⇒ 3x+2 = 30
Since the bases are equal, let us equate the exponents
⇒ x + 2 = 0
⇒ x = -2
Thus, the value of x is -2
Question 10. If 49392 = a4b2c3, find the values of a, b, and c where a, b and c are different positive primes.
Solution:
Let us first find out prime factorization of 49392

Thus, 49392 = 24 × 32 × 73
Where 2, 3 and 7 are positive primes
49392 = 243273 = a4b2c3
Thus, on comparing, we get
a = 2,b = 3 and c = 7
Thus, the values of a, b and c are 2, 3, 7 respectively.
Question 11. If 1176 = 2a3b7c, find a, b and c.
Solution:
Given 1176 = 2a3b7c
Let us first find out prime factorization of 1176

Thus, 1176 = 23 × 31 × 72
1176 = 233172 = 2a3b7c
Thus, on comparing, we get
a = 3, b = 1, c = 2
Thus, the values of a, b and c are 3, 1, 2 respectively.
Question 12. Given 4725 = 3a5b7c, find
(i) the integral values of a, b and c
(ii) the value of 2-a3b7c
Solution:
Given 4725 = 3a5b7c
(i) Let us first find out prime factorization of 4725

Thus, 4725 = 33 × 52 × 71
4725 = 335271 = 3a5b7c
Thus, on comparing, we get
a = 3,b = 2,c = 1
Thus, the values of a, b and c are 3,2,1 respectively.
(ii) Here a = 3, b = 2, c = 1
On substituting these values in 2-a3b7c
2-a3b7c= 2-3×32×71
= 1/8 × 9 × 7 = 63/8
Thus, the value of 2-a3b7c is 63/8
Question 13. If a = xyp-1, b = xyq-1, c = xyr-1, prove that aq-rbr-pcp-q = 1.
Solution:
Given a = xyp-1, b = xyq-1, c = xyr-1
aq-rbr-pcp-q=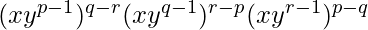
= 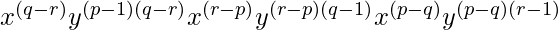
= xq-r+r-p+p-q y(p-1)(q-r)+(r-p)(q-1)+(p-q)(r-1)
= xq-r+r-p+p-q ypq-q-pr+r+rq-r-pq+p+pr-p-qr+q
= x0y0
= 1
Thus, we proved that aq-rbr-pcp-q = 1
Share your thoughts in the comments
Please Login to comment...