Question 25. In an A.P. the first term is 22, nth term is –11 and the sum of first n term is 66. Find n and the d, the common difference.
Solution:
Given A.P. has first term(a) = 22, nth term(an) = –11 and sum(Sn) = 123.
Now by using the formula of sum of n terms of an A.P.
Sn = n[a + an] / 2
=> 66 = n[22 + (−11)]/2
=> 66 = n[22 − 11]/2
=> 11n = 132
=> n = 12
By using the formula of nth term of an A.P.
an = a + (n – 1)d
=> −11 = 22 + (12 – 1)d
=> 11d = –33
=> d = –3
Hence, the number of terms of given A.P. is 12 and common difference is –3.
Question 26. The first and the last terms of an A.P. are 7 and 49 respectively. If sum of all its terms is 420, find the common difference.
Solution:
Given A.P. has first term(a) = 7, last term(an) = 49 and sum(Sn) = 420.
Now by using the formula of sum of n terms of an A.P.
Sn = n[a + an] / 2
So,
=> 420 = n[7 + 49]/2
=> 28n = 420
=> n = 15
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
=> 49 = 7 + (15 – 1)d
=> 14d = 42
=> d = 3
Hence, the common difference of the given A.P. is 3.
Question 27. The first and the last terms of an A.P are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference.
Solution:
Given A.P. has first term(a) = 5, last term(an) = 45 and sum(Sn) = 400.
Now by using the formula of sum of n terms of an A.P.
Sn = n[a + an] / 2
=> 400 = n[5 + 45]/2
=> 25n = 400
=> n = 16
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
=> 45 = 5 + (16 – 1)d
=> 15d = 40
=> d = 8/3
Hence, the common difference of the given A.P. is 8/3.
Question 28. The sum of first 9 terms of an A.P. is 162. The ratio of its 6th term to its 13th term is 1: 2. Find the first and 15th term of the A.P.
Solution:
We know sum of n terms of an A.P. is given by Sn = n[2a + (n − 1)d] / 2.
Therefore, Sum of first 9 terms of given A.P. = S9 = 9[2a + (9 − 1)d] / 2 = 162
=> 162 = 9(2a + (9 − 1)d) / 2
=> 2a + 8d = 36
=> a + 4d = 18 …..(1)
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
Given a6 : a13 = 1 : 2,
=> a13 = 2a6
=> a+12d = 2(a + 5d)
=> a+12d = 2a + 10d
=> a = 2d …..(2)
On putting (2) in (1), we get,
=> 2d + 4d = 18
=> 6d = 18
=> d = 3
On putting d = 3 in (2), we get,
a = 2(3) = 6, which is the first term.
Now 15th term, a15 = a + 14d = 6 + 14 × 3 = 6 + 42 = 48
Hence, the first and 15th term of the A.P. are 6 and 48 respectively.
Question 29. If the 10th term of an A.P. is 21 and the sum of its first 10 terms is 120, find its nth term.
Solution:
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
10th term of the given A.P., a10 = 21
=> a + 9d = 21 …..(1)
By using the formula of the sum of n terms of an A.P.
Sn = n[2a + (n − 1)d] / 2.
So,
S10 = 10[2a + (10 − 1)d] / 2
=> 120 = 5(2a + 9d)
=> 2a + 9d = 24 …. (2)
On subtracting (1) from (2), we get
=> 2a + 9d – a – 9d = 24 – 21
=> a = 3
On putting a = 3 in eq(1), we get,
=> 3 + 9d = 21
=> 9d = 18
=> d = 2
So, an = 3 + (n – 1)2
= 3 + 2n – 2
= 2n + 1
Hence, the nth term of the given A.P is 2n + 1.
Question 30. The sum of the first 7 terms of an A.P. is 63 and the sum of its next 7 terms is 161. Find the 28th term of this A.P.
Solution:
Sum of first 7 terms of an A.P., S7 = 63.
And sum of next 7 terms is 161.
So, the sum of first 14 terms, S14 = Sum of first 7 terms + Sum of next 7 terms
S14 = 63 + 161 = 224
By using the formula of the sum of n terms of an A.P.
Sn = n[2a + (n − 1)d] / 2.
So, S7 = 7(2a + (7 − 1)d) / 2
=> 7(2a + 6d) / 2 = 63
=> 2a + 6d = 18 . . . . (1)
Also, S14 = 14(2a + (14 − 1)d) / 2
=> 14(2a+13d)/2 = 224
=> 2a+13d = 32 . . . . (2)
Now, subtracting eq(1) from eq(2), we get
=> 13d – 6d = 32 – 18
=> 7d = 14
=> d = 2
On putting d = 2 in eq(1), we get,
=> 2a + 6(2) = 18
=> 2a = 18 – 12
=> a = 3
Thus, a28 = a + (28 – 1)d = 3 + 27 (2) = 3 + 54 = 57
Hence, the 28th term is 57.
Question 31. The sum of first seven terms of an A.P. is 182. If its 4th and 17th terms are in ratio 1: 5, find the A.P.
Solution:
By using the formula of the sum of n terms of an A.P.
Sn = n[2a + (n − 1)d] / 2.
So, S7 = 7(2a + (7 − 1)d) / 2
=> 7(2a + 6d) = 364
=> 14a + 42d = 364
=> a + 3d = 26 .… (1)
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
We are given, a4 : a17 = 1:5
=> a17 = 5a4
=> a+16d = 5[a + 3d]
=> a + 16d = 5a + 15d
=> 4a = d …. (2)
Using eq(2) in eq(1), we get,
=> a + 3(4a) = 26
=> 13a = 26
=> a = 2
On putting a = 2 in eq(2), we get,
=> d = 8
As the first term of the given A.P. is 2 and
the common difference is 8, So, the A.P. is 2, 10, 18, 26, …..
Question 32. The nth term of an A.P is given by (−4n + 15). Find the sum of first 20 terms of this A.P.
Solution:
We are given the nth term of the A.P., an = −4n + 15.
On putting n = 1 to find the first term of our A.P., a = −4(1) + 15 = 11
On putting n = 20 to find the 20th term of the A.P., a20 = −4(20) + 15 = −65
By using the formula of the sum of first n terms of an A.P.
Sn = n[a + an] / 2.
So, S20 = 20[11 + (−65)] / 2
= 10(−54) = −540
Hence, the sum of first 20 terms of this A.P. is −540.
Question 33. In an A.P. the sum of first ten terms is −150 and the sum of its next 10 term is −550. Find the A.P.
Solution:
Sum of first ten terms, S10 = −150.
Also given, Sum of its next 10 terms = −550
Sum of first 20 terms, S20 = Sum of first 10 terms + Sum of next 10 terms
=> S20 = −150 + (−550) = −700
By using the formula of the sum of n terms of an A.P.
Sn = n[2a + (n − 1)d] / 2.
So, S10 = 10(2a + (10 − 1)d) / 2
=> −150 = 5(2a + 9d)
=> 2a + 9d = –30 ….. (1)
And also, S20 = 20(2a + (20 − 1)d) / 2
=> −700 = 10(2a + 19d)
=> 2a + 19d = −70 ….. (2)
Now, subtracting eq(1) from (2), we get
=> 19d – 9d = –70 – (–30)
=> 10d = –40
=> d = –4
On putting d = –4 in (1), we get,
=> 2a + 9(–4) = –30
=> 2a = 6
=> a = 3
As we have a = 3 and d = –4, hence, the A.P is 3, –1, –5, –9,…..
Question 34. Sum of the first 14 terms of an A.P. is 1505 and its first term is 10. Find its 25th term.
Solution:
Given A.P. has first term(a) = 10 and sum of the first 14 terms, S14 = 1505.
By using the formula of the sum of n terms of an A.P.
Sn = n[2a + (n − 1)d] / 2.
=> S14 = 14(2(10) + (14 − 1)d) / 2 = 1505
=> 7(20 + 13d) = 1505
=> 20 + 13d = 215
=> 13d = 195
=> d =15
We know the 25th term is, a25 = 10 + (25 − 1)15
= 10 + 24(15)
= 370
Hence, the 25th term of the A.P is 370.
Question 35. In an A.P. , the first term is 2, the last term is 29 and the sum of the terms is 155. Find the common difference of the A.P.
Solution:
Given A.P. has first term(a) = 2, last term(an) = 29 and sum(Sn) = 155.
By using the formula of the sum of first n terms of an A.P.
Sn = n[a + an] / 2.
=> 155 = n(2 + 29) / 2
=> 31n = 310
=> n = 10
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
=> 29 = 2 + (10 – 1)d
=> 9d = 27
=> d = 3
Hence, the common difference of the A.P. is 3.
Question 36. The first and the last terms of an A.P. are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?
Solution:
Given A.P. has first term(a) = 17, common difference(d) = 9 and last term(an) = 350.
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
=> 350 = 17 + (n – 1) 9
=> 350 = 17 + 9n – 9
=> 9n = 342
=> n = 38
By using the formula of the sum of first n terms of an A.P.
Sn = n[a + an] / 2.
S38 = 38(17 + 350)/2
= 19(367) = 6973
Hence, the number of terms of the given A.P is 38 and sum is 6973.
Question 37. Find the number of terms of the A.P. –12, –9, –6, . . . , 21. If 1 is added to each term of this A.P., then find the sum of all terms of the A.P. thus obtained.
Solution:
If 1 is added to each term of the A.P. then the new A.P. is –11, –8, –5, . . . , 22.
First term, a = –11 and common difference, d = – 8 – (–11) = 3
And, we know that nth term = an = a + (n – 1)d
=> 22 = –11 + (n – 1)3
=> 3n = 36
=> n = 12
By using the formula of the sum of first n terms of an A.P.
Sn = n[a + an] / 2.
=> S12 = 12[–11 + 22]/2
= 6[11]
= 66
Hence, the sum after adding 1 to each of the terms in the A.P is 66.
Question 38. The sum of the first n terms of an A.P. is 3n2 + 6n. Find the nth term of this A.P.
Solution:
Given Sn = 3n2 + 6n
On putting n = 1, we get the first term(a), S1 = a = 3(1)2 + 6(1) = 9
On putting n = 2 gives S2 = a + a + d = 3(2)2 + 6(2) = 24
=> d = 24 – 2a
=> d = 24 – 18 = 6
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
= 9 + (n – 1)6
= 9 + 6n – 6
= 6n + 3
Hence, the nth term of the given A.P. is 6n + 3.
Question 39. The sum of the first n terms of an A.P. is 5n – n2. Find the nth term of this A.P.
Solution:
Given Sn = 5n – n2,
On putting n = 1, we get the first term(a), S1 = a = 5(1) – (1)2 = 4
On putting n = 2 gives S2 = a + a + d = 5(2) – (2)2 = 6
=> d = 6 – 2a
=> d = 6 – 8 = –2
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
= 4 + (n – 1)(–2)
= 4 – 2n + 2
= 6 – 2n
Hence, the nth term of the given A.P. is 6 – 2n.
Question 40. The sum of the first n terms of an A.P. is 4n2 + 2n. find the nth term of this A.P.
Solution:
Given Sn = 4n2 + 2n,
On putting n = 1, we get the first term(a), S1 = a = 4(1)2 + 2(1) = 6
On putting n = 2 gives S2 = a + a + d = 4(2)2 + 2(2) = 20
=> d = 20 – 2a
=> d = 20–12 = 8
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
= 6 + (n – 1)8
= 6 + 8n – 8
= 8n – 2
Hence, the nth term of the given A.P. is 8n – 2.
Question 41. The sum of first n terms of an A.P. is 3n2 + 4n. find the 25th term of this A.P.
Solution:
Given Sn = 3n2 + 4n,
On putting n = 1, we get the first term(a), S1 = a = 3(1)2 + 4(1) = 7
On putting n = 2 gives S2 = a + a + d = 3(2)2 + 4(2) = 20
=> d = 20 – 2a
=> d = 20–14 = 6
The 25th term of the A.P., a25 = a + (25 – 1)d
= 7 + (24)8
= 7 + 144
= 151
Hence, the 25th term of the A.P. is 151.
Question 42. The sum of first n terms of an A.P. is 5n2 + 3n. If its mth term is 168, find the value of m. Also, find the 20th term of this A.P.
Solution:
Given Sn = 5n2 + 3n,
On putting n = 1, we get the first term(a), S1 = a = 5(1)2 + 3(1) = 8
On putting n = 2 gives S2 = a + a + d = 5(2)2 + 3(2) = 26
=> d = 26 – 2a
=> d = 26 – 16 = 10
The mth term of the A.P., am = a + (m – 1)d = 168
=> 8 + (m – 1)10 = 168
=> (m – 1)10 = 160
=> m – 1 = 16
=> m = 17
20th term of the A.P., a20 = a + 19d
= 8 + 19(10)
= 8 + 190
= 198
Hence, the value of m is 17 and 20th term of the A.P. is 198.
Question 43. The sum of first q terms of an A.P. is 63q – 3q2. If its pth term is –60, find the value of p. Also, find the 11th term of this A.P.
Solution:
Given Sn = 63q – 3q2,
On putting n = 1, we get the first term(a), S1 = a = 63(1) – 3(1)2 = 60.
On putting n = 2 gives S2 = a + a + d = 63(2) – 3(2)2 = 114
=> d = 114 – 2a
=> d = 114 – 120 = –6
The pth term of the A.P., ap = a + (p – 1)d = –60
=> 60 + (p – 1)(–6) = –60
=> (p – 1)(–6) = –120
=> p – 1 = 20
=> p = 21
11th term of the A.P., a11 = a+10d
= 60 + 10(–6)
= 0
Hence, the value of p is 21 and 11th term of the A.P. is 0.
Question 44. The sum of first m terms of an A.P. is 4m2 – m. If its nth term is 107, find the value of n. Also, find the 21st term of this A.P.
Solution:
Given Sm = 4m2 – m,
On putting m = 1, we get the first term(a), S1 = a = 4(1)2 – 1 = 3.
On putting m = 2 gives S2 = a + a + d = 4(2)2 – 2 = 14
=> d = 14 – 2a
=> d = 14 – 6 = 8
The nth term of the A.P., an = a + (n – 1)d = 107
=> 3 + (n – 1)8 = 107
=> 8(n – 1) = 104
=> n – 1 = 13
=> n = 14
21st term of the A.P., a21 = a + 20d
= 3 + 20(8)
= 163
Hence, the value of n is 14 and 21st term of the A.P. is 163.
Question 45. If sum of the first n terms of an A.P. is 4n – n2, then what is the first term? What is the sum of first two terms? What is the second term? Similarly find the 3rd, 10th and nth terms.
Solution:
Given Sn = 4n – n2,
On putting n = 1, we get the first term(a), S1 = a = 4(1) – 12 = 3.
On putting n = 2 gives S2 = a + a + d = 4(2) – 22 = 4
=> d = 4 – 2a
=> d = 4 – 6 = –2
Second term(a2) = a + d = 3 + (–2) = 1
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
= 3 + (n – 1)(–2)
= 5 – 2n
Hence, third term(a3) = 5 – 2(3) = –1
And tenth term(a10) = 5 – 2(10) = –15
Hence, the first term is 3, sum of first two terms is 4, second term is 1
and 3rd, 10th and nth terms are –1, –15 and 5 – 2n respectively.
Question 46. If the sum of first n terms of an A.P. is 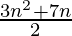 then find its nth term. Hence, write its 20th term.
then find its nth term. Hence, write its 20th term.
Solution:
Given Sn = (3n2 + 7n) / 2,
On putting n = 1, we get the first term(a), S1 = a = [3(1)2 + 7(1)]/2 = 10/2 = 5
On putting n = 2 gives S2 = a + a + d = [3(2)2 + 7(2)]/2 = 26/2 = 13
=> d = 13 – 2a
=> d = 13 – 10 = 3
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
= 5 + (n – 1)3
= 5 + 3n – 3
= 3n + 2
Now we find the 20th term:
a20 = 3(20) + 2
= 60 + 2
= 62
Hence, the nth term of the given A.P. is 3n + 2 and the 20th term is 62
Question 47. In an A.P. the sum of first n terms is 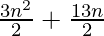 . Find its 25th term.
. Find its 25th term.
Solution:
Given Sn = 3n2/2 + 13n/2,
On putting n = 1, we get the first term(a), S1 = a = 3(1)2/2 + 13(1)/2 = (3 + 13) / 2 = 8
On putting n = 2 gives S2 = a + a + d = 3(2)2/2 + 13(2)/2 = 19
=> d = 19 – 2a
=> d = 19 – 16 = 3
The 25th term of the A.P., a25 = a + (25 – 1)d
= 8 + (24)3
= 6 + 72
= 80
Hence, the 25th term of the given A.P. is 80.
Question 48. Find the sum of all natural numbers between 1 and 100 which are divisible by 3.
Solution:
Natural numbers between 1 and 100 which are divisible by 3 are 3, 6, 9, 12, . . . 99.
These numbers form an A.P. with first term(a) = 3,
Common difference(d) = 6 – 3 = 3 and nth term(an) = 99.
By using the formula of nth term of an A.P.
an = a + (n – 1)d
So,
=> 99 = 3 + (n – 1)3
=> 3(n – 1) = 96
=> n – 1 = 32
=> n = 33
By using the formula of the sum of first n terms of an A.P.
Sn = n[a + an] / 2.
So,
S33 = 33[3 + 99]/2
= 33[51]
= 1683
Hence, the sum of all natural numbers between 1 and 100 which are divisible by 3 is 1683.
Share your thoughts in the comments
Please Login to comment...