Class 10 RD Sharma Solutions – Chapter 5 Trigonometric Ratios – Exercise 5.1 | Set 3

rahulsharma1771996

Question 22. If sinθ = a/b, find secθ + tanθ in terms of a and b.

Solution:

Given:
sinθ = a/b
From Pythagoras theorem,
AC²= BC²+ AB²
b²= a²+ AB²
AB²=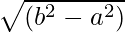 $\sqrt{(b^2-a^2)}$
Now,
= secθ + tanθ
= $\frac{b}{\sqrt(b^2-a^2)}+\frac{a}{\sqrt(b^2-a^2)}$
= $\frac{b+a}{\sqrt(b^2-a^2)}$
= $\frac{(\sqrt(b+a))^2}{\sqrt(b-a)\sqrt(b+a)}$
= $\frac{\sqrt(b+a)}{\sqrt(b-a)}$
= $\sqrt\frac{b+a}{b-a}$

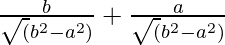
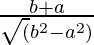
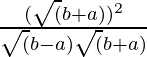
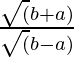
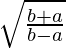
Question 23. If 8tanA = 15, find sin A − cos A.

Solution:

Given:
8tanA = 15
tanA = 15/8
From pythagoras theorem,
AC²= BC²+ AB²
AC²= 15²+ 8²
AC²= 225 + 64 = 289
AC = 17
Now,
= sin A − cos A
= 15/17 – 8/17
= (15 – 8)/17
= 7/17

Question 24. If tanθ = 20/21, show that 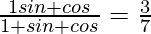$\frac{1−sinθ+cosθ}{1+sinθ+cosθ}=\frac{3}{7}$ .

Solution:

Given: tanθ = 20/21
From Pythagoras theorem,
AC²= BC²+ AB²
AC²= 20²+ 21²
AC²= 400 + 441 = 841
AC = 29
Now, taking LHS
= $\frac{1−sinθ+cosθ}{1+sinθ+cosθ}$
= $\frac{1−\frac{20}{29}+\frac{21}{29}}{1+\frac{20}{29}+\frac{21}{29}}$
= $\frac{29-20+21}{29+20+21}$
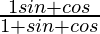
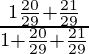
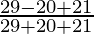
= 30/70
= 3/7

Question 25. If cosec A = 2, find the value of 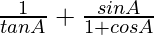$\frac{1}{tanA}+\frac{sinA}{1+cosA}$ .

Solution:

Given:
cosec A = 2
We know
sin A = 1/cosecA = 1/2
And, sin 30° = 1/2
A = 30°
tan30° = 1/√3 and cos30° = √3/2
Now,
= $\frac{1}{tanA}+\frac{sinA}{1+cosA}$
= $\frac{1}{\frac{1}{\sqrt3}}+\frac{\frac{1}{2}}{1+\frac{\sqrt3}{2}}$
= $\sqrt3+\frac{\frac{1}{2}}{\frac{2+\sqrt3}{2}}$
= $\sqrt3+\frac{1}{2+\sqrt3}$
= $\frac{2\sqrt3+3+1}{2+\sqrt3}$
= $\frac{2\sqrt3+4}{2+\sqrt3}$
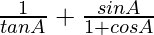
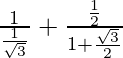
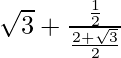
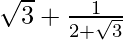
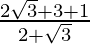
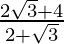
= 2

Question 26. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

Solution:

Let us consider a △ABC
From the figure,
Given,
cos A = cos B
AC/AB = BC/AB
Multiplying both side by AB
(AC/AB) × AB = (BC/AB) × AB
AC = BC
In △ABC, AC = BC So we can say that the triangle is an isosceles triangle,
and in an isosceles triangle we know that if two sides of a triangle are equal,
then the angle opposite to the sides are equal.
Therefore, ∠A =∠B

Question 27. In a Δ ABC, right angled at A, if tanC = √3, find the value of sin B cos C + cos B sin C.

Solution:

In right angled Δ ABC,
Given: tan C = √3
∴AB = √3 and AC = 1
From pythagoras theorem,
BC²= AB²+ AC²
BC²= (√3)²+ 1²
BC²= 3 + 1 = 4
BC = 2
Therefore,
sin B cos C + cos B sin C
= (1/2)(√3/2) + (√3/2)(√3/2)
= 1/4 + 3/4
= 4/4
= 1

Question 28. State whether the following are true or false. Justify your answer.

(i) The value of tan A is always less than 1.

Solution:

FALSE. The value of tan A is not always less than 1.
Consider the Pythagorean triplet, 13, 12, and 5
where, 13 is the hypotenuse
We know
tan A = Perpendicular/Base
Let Perpendicular = 12 and Base = 5
then, tanA = 12/5 = 2.4 which is greater than 1.

(ii) sec A = 12/5 for some value of angle A.

Solution:

TRUE
We have sec A = 12/5 for some value of ∠A
secθ = Hypotenuse/Base
In a right angled triangle, hypotenuse is the greatest side.
So secθ > 1 is valid
Here, secθ = 12/5

(iii) cos A is the abbreviation used for the cosecant of angle A.

Solution:

FALSE
cos A means cosine of ∠A
cos A = Base/Hypotenuse
However,
cosec A = Hypotenuse/Perpendicular

(iv) cot A is the product of cot and A.

Solution:

FALSE
cot A means Cotangent of ∠A
cot A = 1/tanA
Only “cot” doesn’t defines anything.
Hence, cot A is not the product of cot and A.

(v) sinθ = 4/3 for some angle θ.

Solution:

FALSE
sinθ = 4/3 for some value of ∠θ
We have,
sinθ = Perpendicular/Hypotenuse
In a right angled triangle, hypotenuse is the greatest side.
So sinθ is always less than 1.
Here, sinθ = 4/3 = 1.3 which is greater than 1

Question 29. If sinθ = 12/13, find the value of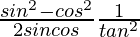 $\frac{sin^2θ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Solution:

Given:
sinθ = 12/13
Using Pythagoras theorem,
AC²= BC²+ AB²
13²= 12²+ AB²
AB²= 169 − 144 = 25
AB = 5
= $\frac{sin^2θ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$
= $\frac{(\frac{12}{13})^2-(\frac{5}{13})^2}{2(\frac{12}{13})(\frac{5}{13})}×\frac{1}{(\frac{12}{5})^2}$
= $\frac{\frac{144}{169}-\frac{25}{169}}{\frac{120}{169}}×\frac{25}{144}$
= $\frac{\frac{144-25}{169}}{\frac{120}{169}}×\frac{25}{144}$
= $\frac{119}{120}×\frac{25}{144}$
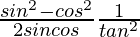
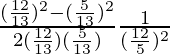
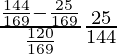
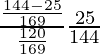
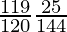
= 595/3456

Question 30. If cosθ = 5/13, find the value of 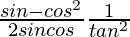$\frac{sinθ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Solution:

Given:
cosθ = 5/13
Using Pythagoras theorem,
AC²= BC²+ AB²
13²= BC²+ 52
BC²= 169 − 25 = 144
BC = 12
= $\frac{sinθ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$
= $\frac{(\frac{12}{13})-(\frac{5}{13})^2}{2(\frac{12}{13})(\frac{5}{13})}×\frac{1}{(\frac{12}{5})^2}$
= $\frac{\frac{144}{169}-\frac{25}{169}}{\frac{120}{169}}×\frac{25}{144}$
= $\frac{\frac{144-25}{169}}{\frac{120}{169}}×\frac{25}{144}$
= $\frac{119}{120}×\frac{25}{144}$
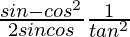
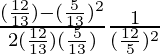
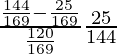
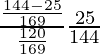
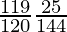
= 595/3456

Question 31. If secA = 5/4, verify that 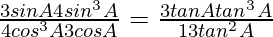$\frac{3sinA−4sin^3A }{4cos^3A−3cosA}=\frac{3tanA−tan^3A}{1−3tan^2A}$ .

Solution:

Given:
secA = 5/4
From pythagoras theorem,
AC²= BC²+ AB²
5²= BC²+ 4²
BC²= 25 − 16 = 9
BC = 3
Now
= $\frac{3sinA−4sin^3A }{4cos^3A−3cosA}=\frac{3tanA−tan^3A}{1−3tan^2A}$
= $\frac{3(\frac{3}{5})−4(\frac{3}{5})^3 }{4(\frac{4}{5})^3−3(\frac{4}{5})}=\frac{3(\frac{3}{4})−(\frac{3}{4})^3}{1−3(\frac{3}{4})^2}$
= $\frac{(\frac{9}{5})−(\frac{108}{125}) }{(\frac{256}{125})−(\frac{12}{5})}=\frac{(\frac{9}{4})−(\frac{27}{64})}{1−(\frac{27}{16})}$
= $\frac{(\frac{225-108}{125}) }{(\frac{256-300}{125})}=\frac{(\frac{144-27}{64})}{(\frac{16-27}{16})}$
= $\frac{(\frac{117}{125}) }{(\frac{-44}{125})}=\frac{(\frac{117}{64})}{(\frac{-11}{16})}$
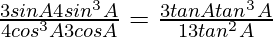
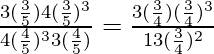
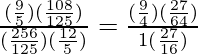
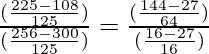
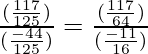
= 117/-44 = 117/(11(4))
= 117/-44 = 117/-44
Hence Proved

Question 32. If sinθ = 3/4, prove that 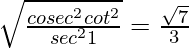$\sqrt\frac{cosec^2θ−cot^2θ}{sec^2θ−1}=\frac{\sqrt 7}{3}$ .

Solution:

Given: sinθ = 3/4
From Pythagoras theorem,
AC²= BC²+ AB²
4²= AB²+ 3²
AB²= 16 – 9 = 7
AB =√7
We have,
$\sqrt\frac{cosec^2θ−cot^2θ}{sec^2θ−1}=\frac{\sqrt 7}{3}$
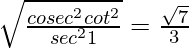
Now squaring both side
= $(\sqrt\frac{cosec^2θ−cot^2θ}{sec^2θ−1})^2=(\frac{\sqrt 7}{3})^2$
= $\frac{cosec^2θ−cot^2θ}{sec^2θ−1}$
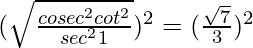
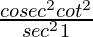
= 7/9
We know
1 + cot²θ = cosec²θ
1 + tan²θ = sec²θ
= 1/tan²θ = 7/9
= $\frac{1}{(\frac{3}{\sqrt7})^2}=\frac{7}{9}$
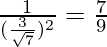
= 7/9 = 7/9
Hence Proved

Question 33. If secA = 17/8, verify that 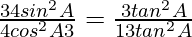$\frac{3−4sin^2A}{4cos^2A−3}=\frac{3−tan^2A}{1−3tan^2A}$ .

Solution:

Given: secA = 17/8
From Pythagoras theorem,
AC²= BC²+ AB²
17²= BC²+ 8²
BC²= 289 − 64 = 225
BC = 15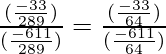 $\frac{(\frac{-33}{289})}{(\frac{-611}{289})}=\frac{(\frac{-33}{64})}{(\frac{-611}{64})}$
We have
$\frac{3−4sin^2A}{4cos^2A−3}=\frac{3−tan^2A}{1−3tan^2A}$
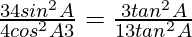
Putting the values of sinA, cosA and tanA in the above equation
= $\frac{3−4\frac{15}{17}^2}{4\frac{8}{17}^2−3}=\frac{3−\frac{15}{8}^2}{1−3\frac{15}{8}^2}$
= $\frac{3−(\frac{900}{289})}{(\frac{256}{289})−3}=\frac{3−(\frac{225}{64})}{1−(\frac{675}{64})}$
= $\frac{(\frac{867-900}{289})}{(\frac{256-867}{289})}=\frac{(\frac{192-225}{64})}{(\frac{64-675}{64})}$
= $\frac{(\frac{-33}{289})}{(\frac{-611}{289})}=\frac{(\frac{-33}{64})}{(\frac{-611}{64})}$
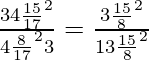
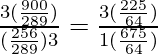
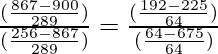
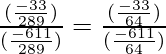
= 33/611 = 33/611
Hence Proved

Question 34. If cotθ = 3/4, prove that 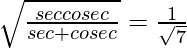$\sqrt\frac{secθ−cosecθ}{secθ+cosecθ}=\frac{1}{\sqrt 7}$ .

Solution:

Given: cotθ = 3/4
tanθ = 4/3
Using the pythagoras theorem
sinθ = 4/5, cosθ = 3/5
cosecθ = 5/4, secθ = 5/3
Now, taking LHS
= $\sqrt\frac{secθ−cosecθ}{secθ+cosecθ}$
= $\sqrt\frac{\frac{5}{3}−\frac{5}{4}}{\frac{5}{3}+\frac{5}{4}}$
= $\sqrt\frac{\frac{5}{12}}{\frac{35}{12}}$
= $\sqrt\frac{5}{35}$
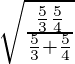
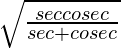
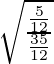
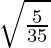
= 1/√7

Question 35. If 3cosθ − 4sinθ = 2cosθ + sinθ, then find tanθ.

Solution:

Given: 3cosθ − 4sinθ = 2cosθ + sinθ
Dividing both equation by cosθ we get,
$3\frac{cosθ}{cosθ}−4\frac{sinθ}{cosθ}=2\frac{cosθ}{cosθ}+\frac{sinθ}{cosθ}$
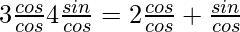
3 – 4tanθ = 2 + tanθ
3 – 2 = 4tanθ + tanθ
tanθ = 1/5

Question 36. If ∠A and ∠B are acute angles such that tan A = tan B, then show that ∠A = ∠B.

Solution:

Let us consider a △ABC
From the figure,
Given:
tan A = tan B
BC/AC = AC/BC
AC²= BC²
AC = BC
In △ABC, AC = BC So we can say that the triangle is an isosceles triangle, √3
and in an isosceles triangle we know that if two sides of a triangle are equal,
then the angle opposite to the sides are equal.
Therefore ∠A =∠B

My Personal Notes

Last Updated : 04 Aug, 2021

Related Articles

Class 10 RD Sharma Solutions – Chapter 5 Trigonometric Ratios – Exercise 5.1 | Set 3

Question 22. If sinθ = a/b, find secθ + tanθ in terms of a and b.

Question 23. If 8tanA = 15, find sin A − cos A.

Question 24. If tanθ = 20/21, show that $\frac{1−sinθ+cosθ}{1+sinθ+cosθ}=\frac{3}{7}$ .

Question 25. If cosec A = 2, find the value of $\frac{1}{tanA}+\frac{sinA}{1+cosA}$ .

Question 26. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

Question 27. In a Δ ABC, right angled at A, if tanC = √3, find the value of sin B cos C + cos B sin C.

Question 28. State whether the following are true or false. Justify your answer.

(i) The value of tan A is always less than 1.

(ii) sec A = 12/5 for some value of angle A.

(iii) cos A is the abbreviation used for the cosecant of angle A.

(iv) cot A is the product of cot and A.

(v) sinθ = 4/3 for some angle θ.

Question 29. If sinθ = 12/13, find the value of $\frac{sin^2θ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Question 30. If cosθ = 5/13, find the value of $\frac{sinθ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Question 31. If secA = 5/4, verify that $\frac{3sinA−4sin^3A }{4cos^3A−3cosA}=\frac{3tanA−tan^3A}{1−3tan^2A}$ .

Question 32. If sinθ = 3/4, prove that $\sqrt\frac{cosec^2θ−cot^2θ}{sec^2θ−1}=\frac{\sqrt 7}{3}$ .

Question 33. If secA = 17/8, verify that $\frac{3−4sin^2A}{4cos^2A−3}=\frac{3−tan^2A}{1−3tan^2A}$ .

Question 34. If cotθ = 3/4, prove that $\sqrt\frac{secθ−cosecθ}{secθ+cosecθ}=\frac{1}{\sqrt 7}$ .

Question 35. If 3cosθ − 4sinθ = 2cosθ + sinθ, then find tanθ.

Question 36. If ∠A and ∠B are acute angles such that tan A = tan B, then show that ∠A = ∠B.

CBSE Class 12 Computer Science

GATE CS & IT 2024

Data Structures & Algorithms in JavaScript - Self Paced

Related Articles

Class 10 RD Sharma Solutions – Chapter 5 Trigonometric Ratios – Exercise 5.1 | Set 3

Question 22. If sinθ = a/b, find secθ + tanθ in terms of a and b.

Question 23. If 8tanA = 15, find sin A − cos A.

Question 24. If tanθ = 20/21, show that .

Question 25. If cosec A = 2, find the value of .

Question 26. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

Question 27. In a Δ ABC, right angled at A, if tanC = √3, find the value of sin B cos C + cos B sin C.

Question 28. State whether the following are true or false. Justify your answer.

(i) The value of tan A is always less than 1.

(ii) sec A = 12/5 for some value of angle A.

(iii) cos A is the abbreviation used for the cosecant of angle A.

(iv) cot A is the product of cot and A.

(v) sinθ = 4/3 for some angle θ.

Question 29. If sinθ = 12/13, find the value of.

Question 30. If cosθ = 5/13, find the value of .

Question 31. If secA = 5/4, verify that .

Question 32. If sinθ = 3/4, prove that .

Question 33. If secA = 17/8, verify that .

Question 34. If cotθ = 3/4, prove that .

Question 35. If 3cosθ − 4sinθ = 2cosθ + sinθ, then find tanθ.

Question 36. If ∠A and ∠B are acute angles such that tan A = tan B, then show that ∠A = ∠B.

Please Login to comment...

CBSE Class 12 Computer Science

GATE CS & IT 2024

Data Structures & Algorithms in JavaScript - Self Paced

Question 24. If tanθ = 20/21, show that $\frac{1−sinθ+cosθ}{1+sinθ+cosθ}=\frac{3}{7}$ .

Question 25. If cosec A = 2, find the value of $\frac{1}{tanA}+\frac{sinA}{1+cosA}$ .

Question 29. If sinθ = 12/13, find the value of $\frac{sin^2θ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Question 30. If cosθ = 5/13, find the value of $\frac{sinθ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Question 31. If secA = 5/4, verify that $\frac{3sinA−4sin^3A }{4cos^3A−3cosA}=\frac{3tanA−tan^3A}{1−3tan^2A}$ .

Question 32. If sinθ = 3/4, prove that $\sqrt\frac{cosec^2θ−cot^2θ}{sec^2θ−1}=\frac{\sqrt 7}{3}$ .

Question 33. If secA = 17/8, verify that $\frac{3−4sin^2A}{4cos^2A−3}=\frac{3−tan^2A}{1−3tan^2A}$ .

Question 34. If cotθ = 3/4, prove that $\sqrt\frac{secθ−cosecθ}{secθ+cosecθ}=\frac{1}{\sqrt 7}$ .