Class 10 RD Sharma Solutions – Chapter 3 Pair of Linear Equations in Two Variables – Exercise 3.1
Last Updated :
18 Mar, 2021
Question 1. Akhila went to a fair in her village. She wanted to enjoy rides on the Giant Wheel and play Hoopla (a game in which you throw a rig on the items in the stall, and if the ring covers any object completely you get it). The number of times she played Hoopla is half the number of rides she had on the giant wheel. Each ride costs ₹3 and a game of hoopla costs ₹4. If she spent ₹20 in the fair, represent this situation algebraically and graphically.
Solution:
Let us assume the number of rides on the wheel to be x
And number of play of Hoopla to be y.
As per the given constraints,
x = 2y ⇒ x – 2y = 0 ….(i)
Cost of ride on wheel at the rate of Rs. 3 = 3x
Cost on Hoopla = 4y
Now, the total cost = Rs. 20
3x + 4y = 20 ….(ii)
Solving the equations (i) and (ii), we get,
Taking three points at-least of each line and connecting them to form a line. The point of intersection holds the solution, in this case.
From equation (i)
x = 2y
Similarly, in equation (ii)
3x + 4y = 20 ⇒ 3x = 20 – 4y
Computing the points for these lines,
Plotting these points and joining the point of intersection, we get the point (4, 2)
The unique solution is (4, 2).
Hence, we obtain, x = 4, y = 2

Question 2. Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” Is not this interesting? Represent this situation algebraically and graphically.
Solution:
Seven years ago :
Let us assume the age of Aftab’s daughter to be x years.
And, the age of Aftab to be y years.
Three years later,
Age of daughter = x + 10 years
Age of Aftab = y + 10 years
According to the given constraints,
y = 7x ⇒ 7x – y = 0 ……….(i)
y + 10 = 3 (x + 10)
=> y + 10 = 3x + 30
3x – y = 10 – 30 = -20
3x – y = -20 ….(ii)
The following equations are obtained :
7x – y = 0
3 x – y = -20
Solving these linear equations graphically :
7x – y = 0 ⇒ y = 7x
Plotting the points of the first line,
For the second equation, we get,
3x – y = -20
y = 3x + 20
Plotting the points of the second line,
Plotting these points and joining the point of intersection, we get the point (5, 35).

Question 3. The path of the train A is given by the equation 3x+4y-12 =0 and the path of another train B is given by the equation 6x+8y-48 =0. Represent this situation graphically.
Solution:
Given constraints are :
Path of A train is 3x + 4y – 12 = 0
and path of B train is 6x + 8y – 48 = 0
Computing the points for the line 3x + 4y- 12 = 0
Also, plotting the points for the second equation 6x+8y-48 =0.
Plotting these points graphically and joining the point of intersection, we get that the pair of lines are parallel.

Question 4. Gloria is walking along the path joining (-2, 3) and (2, -2), while Suresh is walking along the path joining (0, 5) and (4, 0). Represent this situation graphically.
Solution:
We plot the points (-2, 3) and (2, -2) and connect them to form a line.
Also, we plot the points (0, 5), (4, 0) and connect them to obtain another line.
Graphically, we obtain, that these two lines are parallel to each other.

Question 5. On comparing the ratios , and without drawing them, find out whether the lines representing following pairs of linear equations intersect at a point, are parallel or coincide :
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
(ii) 9x + 3y +12 = 0
18x + 6y + 24 = 0
(iii) 6x – 3y +10 = 0
2x – y + 9 = 0
Solution:
(i) We have the following pair of equations,
5x – 4y + 8 = 0
7x + 6y – 9 = 0
We have the following coefficients for these equations,
a1 = 5, b1 = -4, c1= 8
And, a2 = 7, b2= 6 and c2 = -9
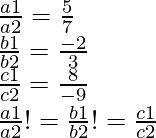
Therefore, these two lines intersect each other at a unique point.
(ii) We have the following pair of equations,
9x + 3y +12 = 0
18x + 6y + 24 = 0
We have the following coefficients for these equations,
a1 = 9, b1 = 3, c1= 12
And, a2 = 18, b2= 6 and c2 = 24
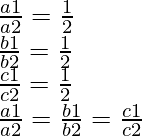
Therefore, these lines are coincident lines.
(iii) We have the following pair of equations,
6x – 3y +10 = 0
2x – y + 9 = 0
We have the following coefficients for these equations,
a1 = 6, b1 = -3, c1= 10
And, a2 = 2, b2= -1 and c2 = 9
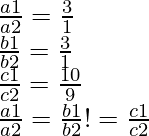
Therefore, these lines are parallel.
Question 6. Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Solution:
We have the equation 2x+3y-8, now the coefficients are a1 = 2 , b1= 3 and c1 = -8 respectively.
(i) For intersecting pair of lines, the ratio of coefficients of the second equation should not be equal to the corresponding coefficients of the first.
So, Let us take a2 = 3, b2 = 4 and c2 = 2
that is, the second equation is 3x+4y+2 = 0
(ii) For parallel lines, we have,
a1/a2 = b1/b2 ≠ c1/c2
Therefore, a2/b2 can be 2/3.
Let us take a2 = 4 and b2 = 6,
that is, the second equation is 4x+6y+5 = 0
(iii) For coincident lines, we have,
a1/a2 = b1/b2 = c1/c2
that is, the second equation is 4x+6y – 16 = 0
Question 7. The cost of 2kg of apples and 1 kg of grapes on a day was found to be Rs. 160. After a month, the cost of 4kg of apples and 2kg of grapes is Rs. 300. Represent the situation algebraically and geo-metrically.
Solution:
Let us assume the cost of 1kg of apples to be Rs. x
And, the cost of 1kg of grapes to be Rs. y
Now according to the given constraints, we obtain the following set of equations :
2x + y = 160
4x + 2y = 300
Now 2x + y = 160
y = 160 – 2x
Obtaining the points for this line :
The second equation, is 4x + 2y = 300
=> 2x + y = 150
=> y = 150 – 2x
Obtaining the points for this line :
Graphically, we obtain, that these two lines are parallel to each other.

Share your thoughts in the comments
Please Login to comment...