Question 1. Apply division algorithm to find the quotient q(x) and remainder r(x) on dividing f(x) by g(x) in each of the following:
(i) f(x) = x3 – 6x2 + 11x – 6, g(x) = x2 + x + 1
(ii) f(x) = 10x4 + 17x3 – 62x2 + 30x – 105, g(x) = 2x2 + 7x + 1
(iii) f(x) = 4x3 + 8x2 + 8x + 7, g(x) = 2x2 – x + 1
(iv) f(x) = 15x3 – 20x2 + 13x – 12, g(x) = x2 – 2x + 2
Solution:
(i) Here we have to divide f(x) = x3 – 6x2 + 11x – 6 by g(x) = x2 + x + 1
So, to get quotient q(x) and remainder r(x), we use division algorithm

Therefore,
Remainder r(x) = 17x – 1
Quotient q(x) = x – 7
(ii) Here we have to divide f(x) = 10x4 + 17x3 – 62x2 + 30x – 105 by g(x) = 2x2 + 7x + 1
So, to get quotient q(x) and remainder r(x), we use division algorithm

Therefore,
Remainder r(x) = 53x – 1
Quotient q(x) = 5x2 – 9x – 2
(iii) Here we have to divide f(x) = 4x3 + 8x2 + 8x + 7 by g(x) =2x2 – x + 1
So, to get quotient q(x) and remainder r(x), we use division algorithm

Therefore,
Remainder r(x) = 11x + 2
Quotient q(x) = 2x – 5
(iv) f(x) = 15x3 – 20x2 + 13x – 12, g(x) = x2 – 2x + 2
Here we have to divide f(x) = 15x3 – 20x2 + 13x – 12 by g(x) = x2 – 2x + 2
So, to get quotient q(x) and remainder r(x), we use division algorithm

Therefore,
Remainder r(x) = 3x + 32
Quotient q(x) = 15x + 10
Question 2. Check whether the first polynomial is a factor of the second polynomial by applying the division algorithm:
(i) g(t) = t2 – 3; f(t) = 2t4 + 3t3 – 2t2 – 9t – 12
(ii) g(x) = x2 – 3x + 1; f(x) = x5 – 4x3 + x2 + 3x + 1
(iii) g(x) = 2x2 – x + 3; f(x) = 6x5 − x4 + 4x3 – 5x2 – x – 15
Solution:
(i) Here, we have to check whether g(t) = t2 – 3 is a factor of f(t) = 2t4 + 3t3 – 2t2 – 9t – 12
So, by using division algorithm, we get

As the remainder left is 0.
Therefore,
g(t) = t2 – 3 is a factor of f(t) = 2t4 + 3t3 – 2t2 – 9t – 12
(ii) Here, we have to check whether g(x) = x2 – 3x + 1 is a factor off(x) = x5 – 4x3 + x2 + 3x + 1
So, by using division algorithm, we get

As the remainder left is 2.
Therefore,
g(x) = x2 – 3x + 1 is not a factor of f(x) = x5 – 4x3 + x2 + 3x + 1
(iii) Here, we have to check whether g(x) = 2x2 – x + 3 is a factor of f(x) = 6x5 − x4 + 4x3 – 5x2 – x – 15
So, by using division algorithm, we get

As the remainder left is 0.
Therefore,
g(x) = 2x2 – x + 3 is a factor of f(x) = 6x5 − x4 + 4x3 – 5x2 – x – 15
Question 3. Obtain all zeroes of the polynomial f(x) = f(x) = 2x4 + x3 – 14x2 – 19x – 6, if two of its zeroes are -2 and -1.
Solution:
Given: f(x) = 2x4 + x3 – 14x2 – 19x – 6
Here we have given the two zeroes of the polynomial that are -2 and -1,
Hence, its factors will be (x + 2) and (x + 1)
Further,
(x + 2)(x + 1) = x2 + x + 2x + 2 = x2 + 3x + 2
So, by using division algorithm, we get

f(x) = 2x4 + x3 – 14x2 – 19x – 6 = (2x2 – 5x – 3)(x2 + 3x + 2)
= (2x + 1)(x – 3)(x + 2)(x + 1)
Hence, the factors of f(x) = 2x4 + x3 – 14x2 – 19x – 6 are (2x + 1), (x – 3), (x + 2), (x + 1)
Therefore, the zeroes of the polynomial are -1/2, 3, -2, -1
Question 4. Obtain all zeroes of f(x) = x3 + 13x2 + 32x + 20, if one of its zeroes is -2.
Solution:
We have been given the zero of the polynomial f(x) = x3 + 13x2 + 32x + 20 is -2.
Hence, its factor is (x + 2).
So, by using division algorithm, we get

Thus,
f(x) = x3 + 13x2 + 32x + 20
= (x2 + 11x + 10)(x + 2)
= (x2 + 10x + x + 10)(x + 2)
= (x + 10)(x + 1)(x + 2)
Hence, the factors of f(x) = x3 + 13x2 + 32x + 20 are (x + 10), (x + 1), (x + 2)
Thus, the zeroes of the polynomial are -1, -10, -2.
Question 5. Obtain all zeroes of the polynomial f(x) = x4 – 3x3 – x2 + 9x – 6, if the two of its zeroes are -√3 and √3.
Solution:
Here, we are given two zeros of the polynomial f(x) = x4 – 3x3 – x2 + 9x – 6 that are -√3 and √3.
Thus, the factors are (x + √3)(x − √3) ⇒ x2 – 3.
So, by using division algorithm, we get

Hence,
f(x) = x4 – 3x2 – x2 + 9x – 6 = (x2 – 3)(x2 – 3x + 2)
(x + √3)(x – √3)(x2 – 2x – 2 + 2)
= (x + √3)(x – √3)(x – 1)(x – 2)
Thus, the factors of f(x) = x4 – 3x3 – x2 + 9x – 6 are (x + √3)(x – √3)(x – 1)(x – 2).
Therefore, the zeroes of the polynomial are -√3, √3, 1, 2.
Question 6. Obtain all zeroes of the polynomial f(x) = 2x4 – 2x3 – 7x2 + x – 1, if the two of its zeroes are -√3/2 and √3/2.
Solution:
Here, we are given two zeros of the polynomial f(x) = 2x4 – 2x3 – 7x2 + x – 1 that are -√3/2 and √3/2.
Thus, the factors are 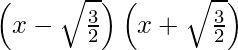 ⇒ x2 – 3/2.
⇒ x2 – 3/2.
So, by using division algorithm, we get

Hence,
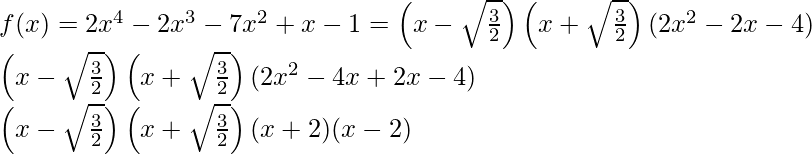
Factors of f(x) = 2x4 – 2x3 – 7x2 + x – 1 are 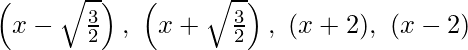 .
.
Thus, the zeroes of the polynomial are -1, 2, -√3/2 and √3/2.
Question 7. Find all the zeroes of the polynomial x4 + x3 – 34x2 – 4x + 120, if the two of its zeroes are 2 and – 2.
Solution:
Here, we are given two zeros of the polynomial x4 + x3 – 34x2 – 4x + 120 that are 2 and -2.
Thus, the factors are (x + 2)(x – 2)⇒ x2 – 4.
So, by using division algorithm, we get

Hence,
x4 + x3 – 34x2 – 4x + 120 = (x2 – 4)(x2 + x – 30)
= (x – 2)(x + 2)(x2 + 6x – 5x – 30)
= (x – 2)(x + 2)(x + 6)(x – 5)
So, the factors of x4 + x3 – 34x2 – 4x + 120 are (x – 2), (x + 2), (x + 6), (x – 5)
Thus, the zeroes of the polynomial = x = 2, – 2, – 6, 5
Question 8. Find all the zeroes of the polynomial 2x4 + 7x3 – 19x2 – 14x + 30, if the two of its zeroes are √2 and -√2.
Solution:
Here, we are given two zeros of the polynomial 2x4 + 7x3 – 19x2 – 14x + 302 that are √2 and -√2.
Thus, the factors are (x + √2)(x – √2) ⇒ x2 – 2.
So, by using division algorithm, we get

Hence,
2x4 + 7x3 – 19x2 – 14x + 30 = (x2 – 2)(2x2 + 7x – 15)
= (2x2 + 10x – 3x – 15)(x + √2)(x – √2)
= (2x – 3)(x + 5)(x + √2)(x – √2)
So, the factors of 2x4 + 7x3 – 19x2 – 14x + 30 are (2x – 3), (x + 5), (x + √2), (x – √2)
Thus, the zeroes of the polynomial is √2, -√2, -5, 3/2.
Question 9. Find all the zeroes of the polynomial f(x) = 2x3 + x2 – 6x – 3, if two of its zeroes are -√3 and √3.
Solution:
Here, we are given two zeros of the polynomial f(x) = 2x3 + x2 – 6x – 3 that are -√3 and √3.
Thus, the factors are (x + √3)(x – √3) ⇒ x2 – 3.
So, by using division algorithm, we get

Hence,
f(x) = 2x3 + x2 – 6x – 3
= (x2 – 3)(2x + 1)
= (x + √3)(x – √3)(2x + 1)
Factors of f(x) = 2x3 + x2 – 6x – 3 are (x + √3), (x – √3), 2x + 1
Thus, the zeroes for the given polynomial are √3, -√3, -1/2
Question 10. Find all the zeroes of the polynomial f(x) = x3 + 3x2 – 2x – 6, if the two of its zeroes are √2 and -√2.
Solution:
Here, we are given two zeros of the polynomial f(x) = x3 + 3x2 – 2x – 6 that are √2 and -√2.
Thus, the factors are (x + √2)(x – √2)⇒ x2 – 2.
So, by using division algorithm, we get

Hence,
f(x) = x3 + 3x2 – 2x – 6
= (x2 – 2)(x + 3)
= (x + √2)(x – √2)(x + 3)
Factors of f(x) = x3 + 3x2 – 2x – 6 are (x + √2), (x – √2), (x + 3)
Thus, the zeroes of the given polynomial is -√2, √2, and – 3.
Question 11. What must be added to the polynomial f(x) = x4 + 2x3 – 2x2 + x − 1 so that the resulting polynomial is exactly divisible by g(x) = x2 + 2x − 3.
Solution:
Here we have to add to the polynomial f(x) = x4 + 2x3 – 2x2 + x − 1 so that the
resulting polynomial is exactly divisible by g(x) = x2 + 2x − 3.
So, divide f(x) = x4 + 2x3 – 2x2 + x − 1 by g(x) = x2 + 2x − 3 to get the answer.

As the remainder left is (x – 2) to get the resulting polynomial exactly divisible by
g(x) = x2 + 2x − 3 we must add (x – 2) to f(x) = x4 + 2x3 – 2x2 + x − 1.
Question 12. What must be subtracted from the polynomial f(x) = x4 + 2x3 – 13x2 –12x + 21 so that the resulting polynomial is exactly divisible by g(x) = x2 – 4x + 3.
Solution:
Here we have to subtract to the polynomial f(x) = x4 + 2x3 – 13x2 – 12x + 21
so that the resulting polynomial is exactly divisible by g(x) = x2 – 4x + 3.
So, divide f(x) = x4 + 2x3 – 13x2 – 12x + 21 by g(x) = x2 – 4x + 3 to get the answer.

As the remainder left is (2x – 3) to get the resulting polynomial exactly divisible by
g(x) = x2 – 4x + 3 we must add (2x – 3) to f(x) = x4 + 2x3 – 13x2 – 12x + 21.
Question 13. Given that √2 is a zero of the cubic polynomial f(x) = 6x3 + √2x2– 10x – 4√2, find its other two zeroes.
Solution:
Here, we are given that √2 is the zero of the cubic polynomial
f(x) = 6x3 + √2x2– 10x – 4√2, thus, factor of the polynomial is (x – √2)
So, by using division algorithm, we get

Hence,
f(x) = 6x3 + √2x2 – 10x – 4√2
= (x – √2)(6x2 + 7√2x + 4)
= (x – √2)(6x2 + 4√2x + 3√2x + 4)
= (x – √2)(3x + 2√2)(2x + √2)
The factors of f(x) = 6x3 + √2x2– 10x – 4√2 are (x – √2), (3x + 2√2), (2x + √2)
Therefore, the zeros of the polynomial are -2√2/3, -√2/2, √2
Question 14. Given that x – √5 is a factor of the cubic polynomial x3 – 3√5x2 + 13x – 3√5, find all the zeroes of the polynomial.
Solution:
Here, we have x – √5 as factor of the cubic polynomial x3 – 3√5x2 + 13x – 3√5
To find all the zeros of the polynomial, we have to divide the polynomial x3 – 3√5x2 + 13x – 3√5 by the factor x – √5

Hence,
x3 – 3√5x2 + 13x – 3√5
= (x – √5)(x2 – 2√5 + 3)
= (x – √5)(x – (√5 + √2))(x – (√5 – √2))
So, the factors of the cubic polynomial x3 – 3√5x2 + 13x – 3√5 are (x – √5), (x – (√5 + √2)), (x – (√5 – √2))
Therefore, the zero of the polynomial are √5, (√5 – √2), (√5 + √2)
Share your thoughts in the comments
Please Login to comment...