Class 9 RD Sharma Solutions – Chapter 6 Factorisation of Polynomials- Exercise 6.3
Last Updated :
11 Feb, 2021
In each of the following using the remainder theorem, find the reminder when f(x) is divided by g(x)and verify by actual division:(1-8)
Question 1. f(x) = x3+4x2-3x+10, g(x) = x+4
Solution:
Given:f(x)=x3+4x2-3x+10, g(x)=x+4
from, the remainder theorem when f(x) is divided by g(x) =x-(-4) the remainder will be equal to f(-4).
Let, g(x)=0
⇒ x+4=0
⇒ x = -4
Substitute the value of x in f(x)
f(-4)=(-4)3+4(-4)2-3(-4)+10
= -64+(4*16)+12+10
= -64 +64 +12+10
= 22
Therefore, the remainder is 22.
Question 2. f(x)=4x4-3x3-2x2+x-7, g(x) =x-1
Solution:
Given:f(x)= 4x4-3x3-2x2+x-7, g(x)=x-1
from, the remainder theorem when f(x) is divided by g(x) = x-(1) the remainder will be equal to f(1)
Let, g(x)=0
⇒ x-1=0
⇒ x=1
Substitute the value of x in f(x)
f(1)= 4(1)4-3(1)3-2(1)2+1-7
= 4-3-2+1-7
= 5-12
= -7
Therefore, the reminder is 7.
Question 3. f(x)=2x4-6x3+2x2-x+2, g(x)=x+2
Solution:
Given: f(x)=2x4-6x3+2x2-x+2, g(x)=x+2
from, the remainder theorem when f(x) is divided by g(x) = x-(-2) the remainder will be equal to f(-2)
Let, g(x)=0
⇒ x+2=0
⇒ x=-2
Substitute the value of x in f(x)
f(-2)=2(-2)4-6(-2)3+2(-2)2-(-2)+2
= (2*16)-(6*(-8))+(2*4)+2+2
= 32+48+8+2+2
= 92
Therefore, the reminder is 92.
Question 4. f(x)=4x3-12x2+14x-3, g(x)=2x-1
Solution:
Given:f(x)=4x3-12x2+14x-3, g(x)=2x-1
from, the remainder theorem when f(x) is divided by g(x) = 2(x-1/2) the remainder will be equal to f(1\2)
Let, g(x)=0
⇒ 2x-1=0
⇒ x=-1/2
Substitute the value of x in f(x)
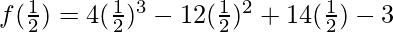
=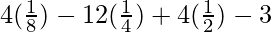
=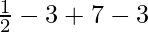
=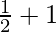
=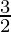
Therefore, the reminder is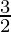
Question 5. f(x)=x3-6x2+2x-4, g(x)=1-2x
Solution:
Given:f(x)=x3-6x2+2x-4, g(x)=1-2x
from, the remainder theorem when f(x) is divided by g(x) = -2(x-1/2) the remainder will be equal to f(1\2)
Let, g(x)=0
⇒ 1-2x=0
⇒ x=1/2
substitute the value of x in f(x)
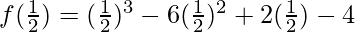
=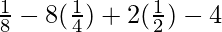
=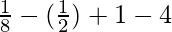
=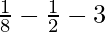
Taking L.C.M
=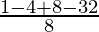
=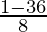
=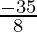
Therefore, the remainder is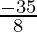
Question 6. f(x)=x4-3x2+4, g(x)=x-2
Solution:
Given:f(x)=x4-3x2+4, g(x)=x-2
from, the remainder theorem when f(x) is divided by g(x) = x-(2) the remainder will be equal to f(2)
Let, g(x)=0
⇒ x-2=0
⇒ x=2
Substitute the value of x in f(x)
f(2)=24-3(2)2+4
= 16-3(4) + 4
= 16 – 12 + 4
= 20 – 12
= 8
Therefore, the remainder is 8
Question 7. f(x)=9x3-3x2+x-5, g(x)=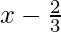
Solution:
Given:f(x)=9x3-3x2+x-5, g(x)=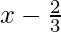
from, the remainder theorem when f(x) is divided by g(x) = x-(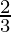 ) the remainder will be equal to f(
) the remainder will be equal to f(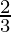 )
)
Let, g(x)=0
⇒ x-2/3=0
⇒ x=2/3
substitute the value of x in f(x)
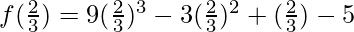
=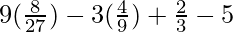
=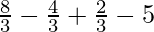
=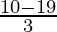
= -3
Therefore, the remainder is -3
Question 8. f(x) =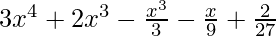 , g(x) =
, g(x) =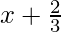
Solution:
Given: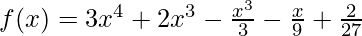 ,
,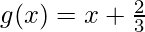
from, the remainder theorem when f(x) is divided by g(x) = x-(-\frac23) the remainder will be equal to f(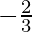 )
)
substitute the value of x in f(x)
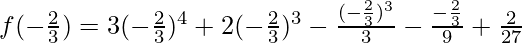
=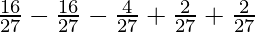
=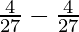
= 0
Therefore, the remainder is 0
Question 9. If the polynomial2x3+ax2+3x-5 andx3+x2-4x+a leave the same reminder when divided by x-2, Find the value of a .
Solution:
Given:f(x)=2x3+ax2+3x-5,p(x)=x3+x2-4x+a
The remainder are f(2) and p(2) when f(x) and p(x) are divided by x-2
We know that,
f(2) = p(2) (given in problem)
we need to calculate f(2) and p(2)
for, f(2)
substitute (x=2) in f(x)
f(2)=2(2)3+a(2)2+3(2)-5
= 16+4a+1
= 4a+17 ———- 1
for, p(2)
Substitute (x=2) in p(x)
p(2)=23+22-4(2)+a
= 8+4-8+a
= 4+a ———– 2
Since, f(2) = p(2)
Equate eq1 and eq2
⇒ 4a+17 = 4+a
⇒ 3a = -13
⇒ a = -13/3
The value of a = -13/3
Question 10. If the polynomialsax3+3x2-3 and2x3-5x+a when divided by (x-4) leave the reminders as R1 and R2 respectively. Find the values of a in each of the following cases, if
1. R1 = R2
2. R1+R2=0
3. 2R1-R2=0
Solution:
The polynomials are f(x)=ax3+3x2-3,p(x)=2x3-5x+a
let,
R1 is the reminder when f(x) is divided by x-4
⇒ R1=f(4)
⇒ R1=a(4)3 + 3(4)2 -3
= 64a + 48 – 3
= 64a + 45 —————– 1
Now, let
R2 is the reminder when p(x) is divided by x-4
⇒ R2=p(4)
⇒ R2=2(4)3-5(4)+a
= 128-20+a
= 108 +a ——————— 2
1. Given, R1 = R2
⇒ 64a + 45 = 108 +a
⇒ 63a=63
⇒ a =1
2. Given, R1+R2 =0
⇒ 64a + 45 + 108 +a = 0
⇒ 65a + 153 = 0
⇒ a = -153/65
3. Given, 2R1-R2 =0
⇒2( 64a + 45)- (108 +a) =0
⇒ 128a + 90 – 108 -a =0
⇒ 127a – 18 =0
⇒ a =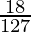
Question 11. If the polynomialsax3+3x2-13 and2x3-5x+a when divided by (x-2) leave the same reminder, find the value of a.
Solution:
Given:f(x)=ax3+3x2-13,p(x)=2x3-5x+a
Equate x-2 to zero
⇒ x=2
Substitute the value of x in f(x) and p(x)
f(2)=a(2)3+3(2)2-13
= 8a+12-13
= 8a-1 ————– 1
p(2)=2(2)3-5(2)+a
= 16-10+a
= 6 + a ————- 2
f(2) = p(2)
⇒ 8a-1 = 6+a
⇒ 7a = 7
⇒ a =1
The value of a is 1
Question 12. Find the reminder whenf(x)=(x)3+3(x)2+3(x)+1 is divided by,
1. x+1
2. x – 1/2
3. x
4. x+π
5. 5+2x
Solution:
Given:f(x)=x3+3x2+3x+1
by reminder theorem
1. x+1 = 0
x=-1
Substitute the value of x in f(x)
f(-1)=(-1)3+3(-1)2+3(-1)+1
= -1+3-3+1
=0
2. x-1/2 =0
x = 1/2
Substitute the value of x in f(x)
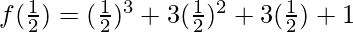
=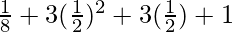
=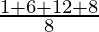
=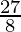
3. x = 0
Substitute the value of x in f(x)
f(0)=(0)3+3(0)2+3(0)+1
= 0 + 0+0+1
= 1
4. x+π =0
x = -π
Substitute the value of x in f(x)
f(-π)=(-π)3+3(-π)2+3(-π)+1
=-π3+3π2-3π +1
5. 5+2x =0
x = -5/2
Substitute the value of x in f(x)
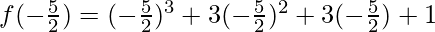
=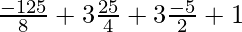
Taking L.C.M
=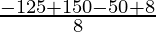
=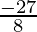
Share your thoughts in the comments
Please Login to comment...