Class 10 RD Sharma Solutions – Chapter 15 Areas Related to Circles – Exercise 15.1 | Set 2

Question 11. The radii of two circles are 19 cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of the circumference of two circles. 

Solution:

Radius of circle 1 = r₁ = 19 cm

Radius of circle 2 = r₂ = 9 cm

So, C₁ = 2πr_1, C₂ = 2πr₂

C = C₁ + C₂

2πr = 2πr₁ + 2πr₂

r = r₁ + r₂ 

r = 19 + 9

r = 28 cm

Therefore, the radius of the circle = 28 cm

Therefore, area of required circle = πr²

                                                     = (22/7) × 28 × 28 

                                                     = 2464 cm²

Question 12. The area of a circular playground is 22176 m². Find the cost of fencing this ground at the rate of ₹50 per meter.

Solution:

Area of the circular playground = 22176 m²

Area = πr²

πr² = 22176

r² = 22176(7/22) 

    = 7056

r = 84 m

Circumference of the ground = 2πr 

                                               = 2(22/7)84 

                                               = 528 m

Cost of fencing 528 m = ₹50 x 528 

                                   = ₹26400

Therefore, the cost of fencing the ground = ₹26400.

Question 13. The side of a square is 10 cm. Find the area of the circumscribed and inscribed circles. 

Solution:

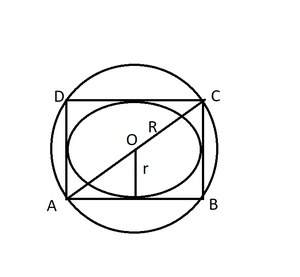
Diagonal of the square = AC = √2 x side

                                     = 10√2 cm

Radius of circumscribed circle = Diagonal/2

R = 5√2cm

R = 7.07cm

Area= πR²

        = (22/7) × 7.07 × 7.07 

        = 157.09 cm² 

Therefore, the Area of the Circumscribed circle = 157.09 cm² 

For inscribed circle diameter of circle = side of square = AB

Radius = side of square/2

           = 10/2 

     r     = 5 m

Area = πr²

        = (22/7) × 5 × 5 

        = 78.5 cm² 

Therefore, the area of the circumscribed circle = 157.09 cm² and the area of the inscribed circle = 78.5 cm².

Question 14. If a square is inscribed in a circle, find the ratio of areas of the circle and the square. 

Solution:

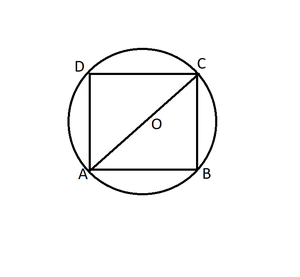
Let side of square AB be x cm which is inscribed in a circle.

Radius of circle (r) = 1/2 (diagonal of square)

                              = 1/2(a√2)

                              r = a/√2

Area of the square = a²

Area of the circle = πr²

                           = π(a²/2)

Ratio of areas = Area of circle:Area of square

                        = π(a²/2) : a²

                                 ⁼ π : 2

Therefore, the ratio of areas of the circle and the square = π : 2

Question 15. The area of circle inscribed in an equilateral triangle is 154 cm². Find the perimeter of the triangle.

Solution:

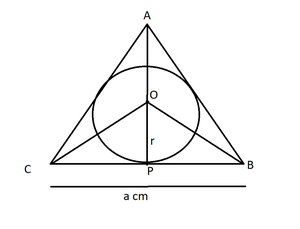
Area of a Circle = πr²

(22/7) × r² = 154

r² = (154 x 7)/22 

   = 7 × 7 

   = 49

r = 7 cm

OP is perpendicular bisector of BC (as BP is tangent and it is a equilateral triangle)

BP = ½ x BC

Consider the side of the equilateral triangle be a cm.

In right-angled triangle OPB

OB² = OP² + BP² (By Pythagoras theorem)

OB² = r² + (a/2)²    (BP is half of a)

OB² = 49 + a²/4

OB = √(49 + a²/2)    ….. (1)

AP = (√3/2)a (height of an equilateral triangle) 

OA = (√3/2)a – r

Similarly 

OB = (√3/2)a – r    …. (2)

From (1) and (2)

Squaring both sides

49 + a²/4 = (3/4)a² + r² – √3ar

r = 7

49 + a²/4 = (3/4)a² + 49 – 7√3a

a²/4- (3/4)a² = -7√3a

Taking 4 as LCM

(a² – 3a²) / 4 = -7√3a

-2a²/4 = -7√3a

a = 14√3 cm

Perimeter of equilateral triangle = 3a

                                                    = 42√3

Therefore, the perimeter of the triangle = 42(1.73) 

                                                             = 72.7 cm

My Personal Notes arrow_drop_up

Save