Question 1. Determine the ratio, in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, -2) and B(3, 7).
Given: 2x + y – 4 = 0 line divides the line segment joining the points A(2, -2) and B(3, 7)
Find: Ratio in which the given line divides the line segment joining the points A and B
So, the co-ordinates of C is ![Rendered by QuickLaTeX.com [\frac{m_1x_2+m_2x_1}{m1+m2},\frac{m_1y_2+m_2y_1}{m1+m2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-01f10e88352946abf8a646c00d77c636_l3.png)
Now, let us considered the ratio is k:1
= ![Rendered by QuickLaTeX.com [\frac{k(3)+1(2)}{k+1},\frac{k(7)+(-2)}{k+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f863f42601709760099e69fb0b78185_l3.png)
= 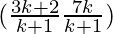
But c lies on 2x+y-4=0
So,
2![Rendered by QuickLaTeX.com [\frac{3k+2}{k+1}+[\frac{7k}{k+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-222199ae2f56244c09b682bb5b408bd6_l3.png) – 4 = 0
– 4 = 0
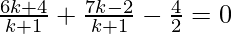
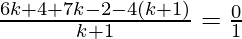
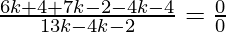
9k = 2
k/1 = 2/9
Hence, the ratio is 2:9
Question 2. Find a relation between x and y, if the points (x, y), (1, 2), and (7, 0) are collinear.
Find: Here, we have to find a relation between x and y, if the points (x, y), (1, 2), and (7, 0) are collinear.
If the given points are collinear then the area of the triangle is 0(created using these points).
So,
Area of triangle = 1/2[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 0
=> x(2 – 0) + 1(0 – y) + 7(y – 2) = 0
=> x(2)+ 1(-y) + 7y – 14 = 0
=> 2x – y + 7y – 14 = 0
=> 2x + 6y – 14 = 0
On dividing by 2 on both sides, we get
x + 3y – 7 = 0
Hence, the required relation is x + 3y – 7 = 0
Question 3. Find the center of a circle passing through the points (6, -6), (3, -7), and (3, 3).
Let us considered point A(6, -6), B(3, -7), and C(3, 3) and P(x, y) is the center of the circle.
So, AP = BP = CP(radii are equal)
Now first we take
AP = BP
√((x2 – x1)2 + (y2 – y1)2) = √((x2 – x1)2 + (y2 – y1)2)
(x – 6)2 + (y + 6)2 = (x – 3)2 + (y + 7)2
x2 + 36 – 12x + y2 + 36 + 12y = x2 + 9 – 6x + y2 + 49 + 14y
36 – 12x + 36 + 12y = 9 – 6x + 49 + 14y
-12x + bx + 12y – 14y + 72 – 58 = 0
-6x – 2y + 14 = 0
6x + 2y – 14 = 0
On divided by 2 on both side, we get
3x + y – 7 = 0 -(1)
Now, we take
BP = CP
√((x2 – x1)2 + (y2 – y1)2) = √((x2 – x1)2 + (y2 – y1)2)
(x – 3)2 + (y + 7)2 = (x – 3)2 + (y – 3)2
y2 + 72 + 2(y)(7) = y2 + 32 – 2(y)(3)
49 + 14y = 9 – 6y
14y + 6y = 9 – 49
20y = -40
y = -40/20
y = -2
Now, on putting value of y = -2 in eq(1), we get
3x – 2 – 7 = 0
3x – 9 = 0
3x = 9
X = 9/3 = 3
Hence, the center P(x, y) = (3, -2)
Question 4. The two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.
Let us considered ABDC is a square, and its two opposite vertices are A(-1, 2) and C(3, 2).
Let point O intersect line AC and BD.
Now, first we will find the coordinate of point O(x, y)
As we know that O is the mid point of line AC,
x = (3 – 1)/2 = 1
y = (2 + 2)/2 = 2
So, the coordinate of point O is (1, 2)
Now we will find the side of the Square
AC = √((3 + 1)2 + (2 – 2)2)
AC = √16 = 4
So in triangle ACD, using hypotenuse theorem, we get
a = 2√2
So, each side of the square is 2√2
For the coordinate of D:
Let us assume that the coordinate of D is (x1, y1).
As we know that the sides of the squares are equal
so, AD = CD
√((x2 – x1)2 + (y2 – y1)2) = √((x2 – x1)2 + (y2 – y1)2)
√(x1 + 1)2 + (y1 – 2)2 = √(x1 – 3)2 + (y1 – 2)2
(x1 + 1)2 + (y1 – 2)2 = (x1 – 3)2 + (y1 – 2)2
(x1 + 1)2 = (x1 – 3)2
x12 + 1 + 2x1 = x12 + 9 – 6x1
1 + 2x1 = 9 – 6x1
2x1 + 6x1 = 9 – 1
8x1 = 8
x1 = 1
Now, CD2 = ((x2 – x1)2 + (y2 – y1)2)
8 = (x1 – 3)2 + (y1 – 2)2
8 = x12 + 9 – 6x1 + y12 + 4 – 4y1
y1 – 2 =2
y1 = 4
So the coordinate of D is (1, 4)
For the coordinate of B:
Let B(x2, y2) and as we know BOD is a line segment so,
1 = x2 + 1/2
x2 = 1
2 = y2 + 4/2
y2 = 0
So the coordinate of B = (1, 0)
Question 5. The class X students school in krishnagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.
(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of ∆PQR, if C is the origin?
Also, calculate the areas of the triangles in these cases. What do you observe?
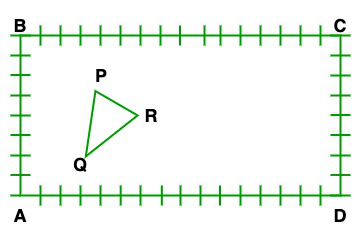
(i) Now taking A as an origin the coordinates of the vertices of the triangle are
P = (4, 6)
Q = (3, 2)
R = (6, 5)
(ii) Now taking C as an origin the coordinates of the vertices of the triangle are
P = (12, 2)
Q = (13, 6)
R = (10, 3)
Finding the area of triangle, when A as a origin the coordinates of the vertices
of the triangle are P(4, 6), Q(3, 2), and R(6, 5)
Area1 = 1/2[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= [4(2 – 5) + 3(5 – 6) + 6(6 – 2)]/2
= [-12 – 3 + 24]/2
= [-15 + 24]/2
= 9/2 sq. unit
Finding the area of triangle, when C as a origin the coordinates of the vertices
of the triangle are P(12, 2), Q(13, 6), and R(10, 3)
Area2 = [12(6 – 3) + 13(3 – 2) + 10(2 – 6)]/2
= [12(3) + 13(1) + 10(-4)]/2
= [36 + 13 – 40]/2
= [49 – 40]/2
= 9/2 Sq.unit
So, here we observed that the Area1 = Area2
Question 6. The vertices of a ∆ABC are A (4, 6), B (1, 5), and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that AD/AB = AE/AC = 1/4. Calculate the area of the ∆ ADE and compare it with the area of ∆ ABC.
Solution:
Given: AD/AB = AE/AC = 1/4
To find: Area of ∆ADE
Since D and E divides AB and AC is the same ratio 1:4 then DE||BC -(Using theorem 6.2)
Now, In ∆ADE and ∆ABC
∠A = ∠A -(Common angle)
∠D = ∠B -(Corresponding angles)
∴∆ADE~∆ABC -(AA similarity)
ar.(ADE)/ar.(ABC) = (AD/AB)2 = 1/16
Area of ∆ABC = 1/2[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= [4(5 – 2) + 1(2 – 6) + 7(6 – 5)]/2
= [4(3) + 1(-4) + 7(1)]/2
= [12 – 4 + 7]/2
= [19 – 4]/2
= 15/2 sq.unit
ar.(ADE)/ar.(ABC) = -(1/10)
ar.(ADE) = (1/16) × ar.(ABC)
ar.(ADE) = (1/16) × (15/2) = 15/32 sq.unit
So, we get
ar.(ADE):ar.(ABC) = 1:16
Question 7.Let A(4, 2), B(6, 5) and C(1, 4) be the vertices of ∆ABC.
(i) The median from A meters BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on the AD, such that AP: PD = 2: 1.
(iii) Find the coordinates of points Q and R on medians BE and CF respectively, such that BQ: QE = 2: 1 and CR: RF = 2: 1.
(iv) What do you observe?
[Note: The points which are common to all the three medians is called centroid and this point divides each median in the ratio 2: 1]
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ∆ABC, find the coordinates of the centroid of the triangles.
Solution:
Given: The vertices of ∆ABC are A(4, 2), B(6, 5) and C(1, 4)
(i) Co-ordinates of D = Midpoint of BC
= ![Rendered by QuickLaTeX.com [\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-19fe05bffdd514d34ce1ab732da61c39_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{6+1}{2},\frac{5+4}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b69998ce80c01d629d9108ca8a9c9bd1_l3.png)
= [7/2, 9/2]
= (3.5, 4.5)
(ii) Co-ordinates of P =![Rendered by QuickLaTeX.com [\frac{m_1x_1+m_2x_2}{2},\frac{m_1y_1+m_2y_2}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ece26b75dea3dd86d70eea5f9cb3a443_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{(3.5)2+1(4)}{2+1},\frac{(4.5)2+1(2)}{2+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a7aefe7a138813fedd019755c2035ed9_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{7+4}{3},\frac{9+2}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b05f24d3fe6b34a022b618650f1e2c2_l3.png)
= [11/3, 11/3]
(iii) Co-ordinates E = Midpoint of AC
= ![Rendered by QuickLaTeX.com [\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-19fe05bffdd514d34ce1ab732da61c39_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{4+1}{2},\frac{2+4}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-375c7993f49ba1f26883b949b22e9962_l3.png)
= (2.5, 3)
(iv) We observe that the points P, Q and R coincide, i.e the medians of AD, BE, and
concurrent at the point [11/3, 11/3]. This point is known as the centroid of the triangle.
(v) As AD is median, thus D is midpoint of BC
So the co-ordinates of D:
= ![Rendered by QuickLaTeX.com [\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-19fe05bffdd514d34ce1ab732da61c39_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{x_2+x_3}{2},\frac{y_2+y_3}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85c0f1fc09646452e52d178bdeb60b6a_l3.png)
Co-ordinates of G:
= [\frac{x_2m_1+m_2x_1 }{m_1+m_2},\frac{y_2m_1+y_1m_12}{m_1+m_2}]
Question 8. ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1), P, Q, R and S are the mid-points of AB, BC, CD, and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Solution:
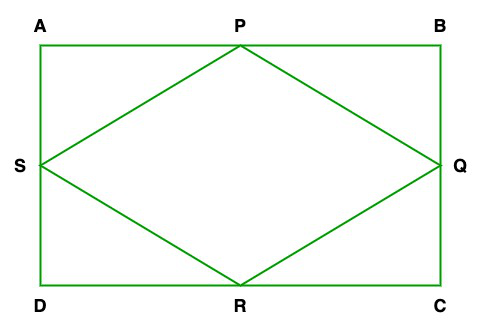
Given: Points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1) and P, Q, R and S are the mid-points of AB, BC, CD, and DA
So,
 = (-2/2, -1, 3/2)
= (-2/2, -1, 3/2)
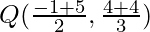 = (4/2, 8/2) = (2, 4)
= (4/2, 8/2) = (2, 4)
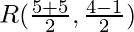 = (10/2, 8/2) = (5, 3/2)
= (10/2, 8/2) = (5, 3/2)
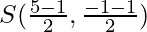 = (4/2, -2/2) = (2, 1)
= (4/2, -2/2) = (2, 1)
So, the length of 

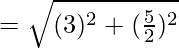
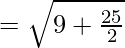
= √(61/4)
The length of 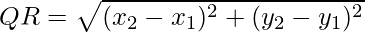
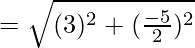

= √(61/4)
The length of 


= √(61/4)
The length of 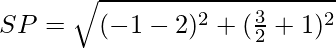
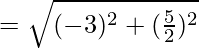

= √(61/4)
The length of the diagonal 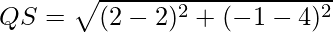
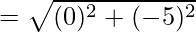
= √25 = 5
The length of the diagonal 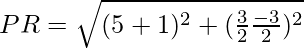
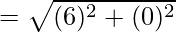
= √36 = 6
Hence, all fours sides are equal(i.e., PQ = QR = RS = SP) but the diagonals are
not equal to each other(i.e. QS ≠ PR).
Therefore, given quadrilateral PQRS is a rhombus.
Share your thoughts in the comments
Please Login to comment...