NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry is developed by the GFG team to assist students in resolving questions related to Coordinate Geometry they may have as they go through problems from the NCERT textbook. To gain a comprehensive understanding of the principles and their real-world applications, it’s essential to read the entire chapter and actively engage in all the associated activities. To assist with this, you will require NCERT Answers for Class 9 Mathematics Chapter 3. All of the problems in this chapter’s exercise from the NCERT textbook are covered in the NCERT Solutions for Class 9 Maths.

Chapter 3 Maths Class 9 serves as a foundational building block for your future studies, as it paves the way for more advanced concepts in higher classes. Dive into the intricacies of Class 9 Maths Chapter 3, and leverage the Coordinate Geometry Class 9 NCERT Solutions to tackle any questions or doubts that may arise along the way.

CBSE Class 9 NCERT Solutions for Maths Chapter 3 Coordinate Geometry covers the following topics:

• Introduction to Coordinate Geometry
• Cartesian Plane
• Plotting Points in the Cartesian Plane
• Slope of a Line
• Distance Formula
• Coordinate Geometry Applications

Class 9 Maths NCERT Solutions Chapter 3 Exercises
NCERT Maths Solutions Class 9 Exercise 3.1 – 2 Questions (1 Short Answer, 1 Long Answer)
NCERT Maths Solutions Class 9 Exercise 3.2 – 2 Questions (2 Short Answers)
NCERT Maths Solutions Class 9 Exercise 3.3 – 2 Questions (1 Short Answer, 1 Long Answer)

NCERT Solutions for Maths Class 9 Chapter 3 Coordinate Geometry: Exercise 3.1

Question 1: How will you describe the position of a table lamp on your study table to another person?

Solution: 

• From the figure above consider the position of the lamp as it is a point on a plane of x and y axis.
• Take two line one perpendicular and one horizontal, consider the perpendicular line as Y-axis and horizontal line as X-axis.
• Take the corner of the table as the origin.
• Measure the distance of lamp from Y-axis and X-axis respectively.
• Write the distance in terms of coordinates (15,25).
• Hence we can find the position of lamp on the table.

Question 2: (Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction.
All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North – South direction and another in the East – West direction. Each cross street is referred to in the following manner : If the 2nd street running in the North – South direction and 5th in the East – West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:
(i) how many cross – streets can be referred to as (4, 3).
(ii) how many cross – streets can be referred to as (3, 4). 

Solution:

• Draw two perpendicular lines that will be referred as the two main roads, mark them as N-S and E-W.
• Take the scale as 1 cm = 200 m as given.
• Mark the intersection of the main road as point C.
• Draw 5-5 parallel line to both the main roads.

(i) We can clearly see that there is only one cross street that can be marked as (3,4).
(ii) We can clearly see that there is only one cross street that can be marked as (4,3).

Coordinate Geometry: Exercise 3.2

Question 1: Write the answer to each of the following questions:

(i) What is the name of the horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
(ii) What is the name of each part of the plane formed by these two lines?
(iii) Write the name of the point where these two lines intersect.

Solution:

(i) Name of the horizontal and vertical lines are:

• The horizontal line drawn on the Cartesian plane is known as x-axis.
• The vertical line drawn on the Cartesian plane is known as y-axis.

(ii) The name of each part of the plane formed by the two lines x-axis and y-axis is called as a quadrant (1/4^th part).                                                               

(iii) Name of the point where there two lines intersect is called the origin(O).

Question 2: See the given figure, and write the following:
(i) The coordinates of B.
(ii) The coordinates of C.
(iii) The point identified by the coordinates (–3, –5).
(iv) The point identified by the coordinates (2, – 4).
(v) The abscissa of the point D.
(vi) The ordinate of the point H.
(vii) The coordinates of the point L.
(viii) The coordinates of the point M.

Solution:

(i) The coordinates of point B is the distance of point B from x-axis and y-axis that is −5 and 2 respectively.
Therefore, the coordinates of point B are (−5, 2).

(ii)  The coordinates of point C is the distance of point C from x-axis and y-axis that is  5 and −5 respectively.
Therefore, the coordinates of point C are (5, −5).

(iii) The point whose x-coordinate and y-coordinate are −3 and −5 respectively is point E.

(iv) The point whose x-coordinate and y-coordinate are 2 and −4 respectively is point G.

(v) The x-coordinate of point D is 6. Therefore, the abscissa of point D is 6.

(vi) The y-coordinate of point H is −3. Therefore, the ordinate of point H is −3.

(vii) The coordinates of point L is the distance of point L from x-axis and y-axis that is 0 and 5 respectively.
Therefore, the coordinates of point L are (0, 5).

(viii) The coordinates of point M is the distance of point M from x-axis and y-axis that is −3 and 0 respectively. Therefore, the coordinates of point M is (−3, 0).

Coordinate Geometry: Exercise 3.3

Question 1: In which quadrant or on which axis do each of the points (– 2,  4), (3,  – 1), (– 1,  0), (1,  2) and (– 3,  – 5) lie? Verify your answer by locating them on the Cartesian plane.

Solution: 

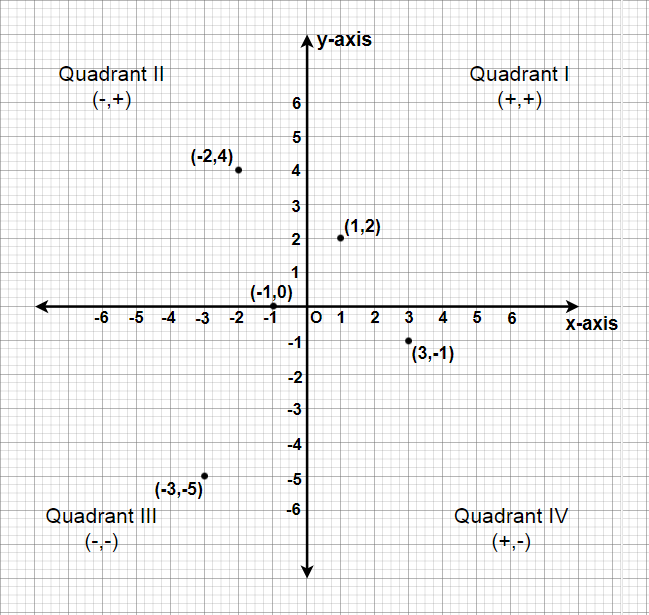
(i) The point (-2, 4) lies in II^nd Quadrant in the Cartesian plane as x coordinate is negative and the y coordinate is positive.

(ii) The point (3, -1) lies in IV^th Quadrant in the Cartesian plane as x coordinate is positive and the y coordinate is negative.

(iii) The point (-1, 0) lies on the negative x-axis and the value of x coordinate is negative.

(iv) The point (1, 2) lies in I^st Quadrant in the Cartesian as both x and y are positive.

(v) The point (-3,-5) lies in the III^rd Quadrant in the Cartesian plane as both x and y are negative.

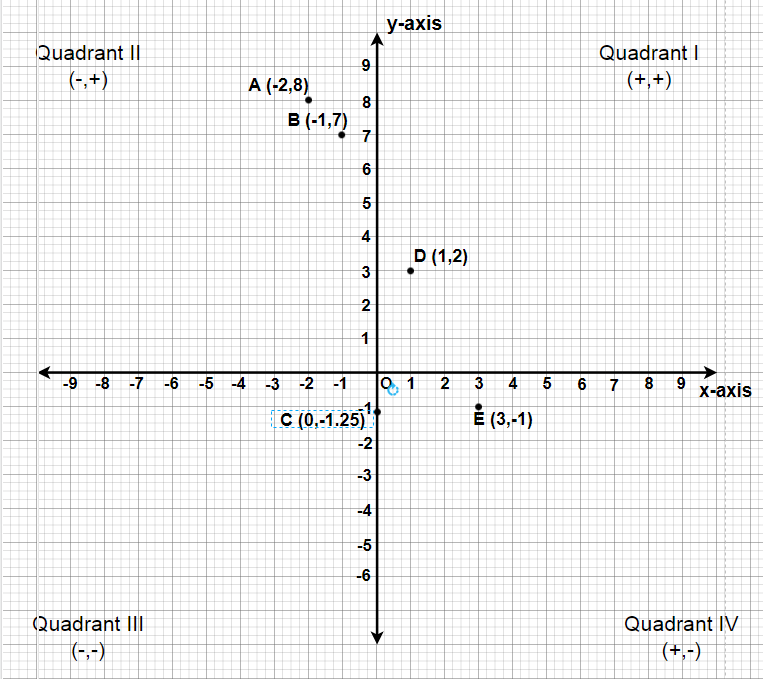
Question 2: Plot the points (x, y) given in the following table on the plane, choosing suitable units of distance on the axes.

Solution:

We have to plot these points A(-2, 8), B(-1, 7), C(0, -1.25), D(1, 3) and E(3, -1).
Steps we have to use to plot these points,

• Let 1 unit represents 1 cm.
• To plot (-2, 8), we take (-2) units on x-axis and (+8) units on y-axis. Now we can plot A (-2, 8), it will lie in quadrant-II.
• To plot (-1, 7), we take (-1) units on x-axis and (+7) units on y-axis. Now we can plot B(-1, 7), it will lie in quadrant-II.
• To plot (0, -1.25), we will proceed (-1.25) units under the x-axis on the y-axis and mark the plot as C(0, -1.25), it will lie on the negative side of y-axis.
• To plot (1, 3), we take (+1) unit on x-axis and (+3) units on y-axis. Now we can plot D(1, 3), it will lie in quadrant-I.
• To plot (3, -1), we take (+3) units on x-axis and (-1) unit on y-axis. Now we can plot the point E(3, -1), it will lie in quadrant-IV.

NCERT Class 9 Chapter 3 Coordinate Geometry Solutions Summary

Class 9 Chapter 3 Maths introduces you to Cartesian coordinates a 2D world with ‘X’ and ‘Y’ axes for precise point location. To assess your understanding, work through the exercises, and use the NCERT Solutions for Class 9 Maths Chapter 3. These expert-crafted NCERT Solutions Class 9 Maths Chapter 3 Coordinate Geometry clarify concepts and lay a strong foundation for advanced learning. Teachers have addressed common challenges faced by students, ensuring swift comprehension. These Class 9 Maths Chapter 3 Solutions help you efficiently solve exercises and offer support from top mathematics educators, guiding you to approach coordinate geometry problems effectively.

Important Topics under NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry

Chapter 3 of the Class 9 Maths syllabus is all about Coordinate Geometry, a crucial link between geometry and algebra. This chapter plays a significant role in building the foundation for more advanced mathematical concepts. Here’s a list of key topics covered in NCERT Class 9 Maths Chapter 3 Coordinate Geometry. A solid grasp of these topics is essential for excelling in exams, as questions related to coordinate geometry are commonly encountered:

• Circle
• Ellipse
• Parabola
• Hyperbola
• Straight Lines

Important Points to Remember:

NCERT Solutions are created for each chapter including coordinate geometry.
These solutions provide in-depth solution to the problems encountered by students in their NCERT textbook.

All the provided solutions are comprehensive and step-by-step, so that students can learn solution with ease.

FAQs on NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry

1. Why is it important to learn Coordinate Geometry?

An introduction to coordinate geometry, or the study of points and lines on a plane using coordinates, is provided in this chapter. To succeed in later maths courses like trigonometry and calculus, it is critical for pupils to comprehend these ideas. Many various kinds of issues can be resolved using coordinate geometry, including determining the separation between two cities, the size of a rectangle, or the pitch of a roof.

2. What topics are covered in NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry?

NCERT Solutions for Class 9 Maths Chapter 3 – Coordinate Geometry covers topics such as

• Introduction to Coordinate Geometry
• Cartesian Plane
• Plotting Points in the Cartesian Plane
• Slope of a Line
• Distance Formula
• Coordinate Geometry Applications

3. How can NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry help me?

NCERT Solutions for Class 9 Maths Chapter 3 – Coordinate Geometry can help you solve the NCERT exercise without any limitations. If you are stuck on a problem you can find its solution in these solutions and free yourself from the frustration of being stuck on some question.

4. How many exercises are there in Class 9 Maths Chapter 3 Coordinate Geometry?

There are 4 exercises in the Class 9 Maths Chapter 3 – Coordinate Geometry which covers all the important topics and sub-topics.

5. Where can I find NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry?

You can find these NCERT Solutions in this article created by our team of experts at GeeksforGeeks.

6. Why Should I Follow CBSE Class 9 Maths Chapter 3 Solutions?

School sessions may not always provide sufficient time for addressing students’ individual doubts and questions. Moreover, it can be challenging for school teachers to attend to the needs of every student simultaneously. By incorporating the NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry into your study routine, you can enjoy the following advantages.

7. What impact can the Class 9 Maths Chapter 3 Solution have?

When studying Class 9, Chapter 3 in Mathematics, easy access to NCERT Solutions for Class 9 Maths Chapter 3 is essential. The most convenient method is to download the Chapter 3 introduction and solutions from this platform, which can be utilized offline and serve as a valuable reference while studying. This solution ensures optimal convenience during your Class 9 Maths NCERT Chapter 3 studies.

8. How can you prepare and complete Coordinate Geometry?

Stay attentive in all your classes, carefully absorb your teacher’s explanations, grasp the concepts, and tackle the exercises. For any lingering questions or uncertainties, turn to NCERT Solutions for Class 9 Maths Chapter 3 to find clear answers.