Class 10 NCERT Solutions- Chapter 6 Triangles – Exercise 6.6

Question 1. In Fig., PS is the bisector of ∠QPR of ΔPQR. Prove that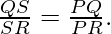

Solution:

Given: PS is angle bisector of ∠QPR.

To prove: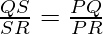 

Construction: Draw RT∥ST to cut OP provided at T.

Proof: since PS∥TR and PR cuts them, hence we have,

∠1 = ∠3           ——[alternate interior angle]  1

∠1 = ∠4           ——[corresponding angle]        2

But ∠1 = ∠2     [given]

From 1 and 2

∴∠3=∠4  

In ∆PTR,

PT = PR    [sides opposite to equal angle are equal]  3

Now In ∆QRT, we have

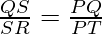                    ———-[by B.P.T]

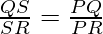   ———[from 3]

Question 2. In Fig., D is a point on hypotenuse AC of ΔABC, such that BD ⊥ AC, DM ⊥ BC and

DN ⊥ AB. Prove that:

(i) DM² = DN.MC

(ii) DN² = DM.AN

Solution:

Given: BD ⊥ AC, DM ⊥ BC and DN ⊥ AB

To prove:  

(i) DM² = DN.MC

(ii) DN² = DM.AN

Proof: we have AB⊥BC and DM⊥BC

So, AB || DM

Similarly, we have CB⊥AB and DN ⊥ AB

Therefore, CB || DN

Hence, BMD DN is a triangle

∴BM=DN or DM=ND  

In ∆BMD,

∠1+ ∠2+ ∠DMB=180           ———–[angle sum property of triangle]

∠1+ ∠2+90=180

∠1+ ∠2=180-90

∠1+ ∠2=90            ——————-1

Similarly, in ∆DMC,

∠3+ ∠4=90°      _______2

∴ from 1 and 2

∠1+ ∠2=∠2+ ∠3

∠1=∠3

From 2 and 3

∠3+ ∠4=∠2+ ∠3

∠4=∠2

Now in ∆BMD and ∆DMC,

∠1=∠3

∠2=∠4

∴∆BMD~∆DMC           ——-(AA similarity criteria)

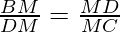
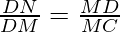
DM²=DN*MC

II) proceeding as in (i), we can prove that ∆BND~∆DNA

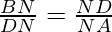
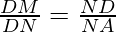      [BN=NA]

DN² = MN*MC

Question 3. In Fig., ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC² = AB² + BC² + 2 BC.BD.

Given: In ∆ABC, ∠ABC > 90° and AD⊥CB provided.

To prove: (AC)²= AB²+BC²+ 2 BC.BD

Proof: In ∆ADB by Pythagoras theorem,

AC²=AD²+AB²

(AC)²= (AD)²+(DB)²        ———1

In ∆ADC by Pythagoras theorem,

(AC)²= (AD)²+(DC)²        ———2

AC²= AD²+DB²         ———1

AC²= AD²+(DB)²+2*DB*BC  

AC²= AD²+(DB)²+BC²+2*DB*BC  

 Question 4. In Figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC² = AB² + BC² – 2BC.BD.

Solution:

Given: In ∆ABC, ∠ABC < 90° and AD ⊥ BC.

To prove: AC² = AB² + BC² – 2*BC.BD

Proof: In triangle ADB, by  Pythagoras theorem

AB²=AD² +BD²       ———1

In triangle ADC, by  Pythagoras theorem

AC²=AD²+DC²       ———2

AC²=AD²+ BC² +BD²

AC²=AD²+ BC² +BD² – 2*BC*BD

AC²=AB²+ BD²+BC² – 2*BC*BD

AC² = AB² + BC² – 2BC.BD

Question 5. In Fig., AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

(i) AC² = AD² + BC.DM + (BC/2)²

(ii) AB² = AD² – BC.DM + (BC/2)²

(iii) AC² + AB² = 2 AD² + 1/2 BC²

Given: In ∆ABC, AD is a median, AM ⊥ BC.  

Prove that:

(i) AC² = AD² + BC.DM + (BC/2)²

(ii) AB² = AD² – BC.DM + (BC/2)²

(iii) AC² + AB² = 2 AD² + 1/2 BC²

Proof: i) In obtuse ∆ADC,∠D>90°

AC² = AD² + DC²+2DC.DM

AC² = AD² +(BC/2)²+2(BC/2).DM

AC² = AD² +(BC/2)2+BC.DM

Or   AC² = AD² +BC.DM+(BC/2)²

II)In acute triangle ABD,

∠D>90°  

AB² = AD² + BD²+2BD.DM

AB² = AD² +(BC/2)²-2(BC/2).DM

AB² = AD² +(BC/2)²-BC.DM

Or  

AB² = AD² -BC.DM +(BC/2)²

iii) Adding i and ii

AC² +AB² =AD²+BC.DM+(BC/2)² +AD² -BC.DM +(BC/2)²

             = 2 AD²+BC/4² +BC/4²

             = 2AD²+1/2.BC/4²

             = 2AD²+ BC²

Question 6. Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.

Solution:

Given: ||gm ABCD and diagonals BD and AC

To prove: AB²+BC²+CD²+AD²=AC²+BD²

Proof: Diagonals of ||gm bisects each other at midpoint  

Solution: In ∆ABC, BO is median

∴AB²+BC²=2BO²+1/2AC²              ———1

In ∆ADC, DO is median

∴AD²+DC² = 2DO²+1/2AC²              ———2

Adding 1 and 2

AB²+BC²+AD²+DC²=2BO²+1/2AC²+2DO²+1/2AC²

             =2.(1/2.BD)² +1/2AC²+2(1/2BD)²+1/2AC²

             =2.BD/4² +1/4AC²+2.BD/4²+1/2AC²

             =BD²/2+1/2AC² +BD²/2+1/2AC²

             =BD²+AC²

Question 7. In Fig., two chords AB and CD intersect each other at the point P. Prove that :

(i) Δ APC ~ Δ DPB  

(ii) AP.PB = CP.DP

Solution:

Given: chords AB and CD intersect each other at the point P.

To prove: (i) Δ APC ~ Δ DPB           (ii) AP.PB = CP.DP

Proof: In ∆ABC and ∆DPB,

∠1=∠2            ——-[vertically opposite angle]

∠A=∠D           ——-[angle in the same segment of circle are equal]

i) ∴∆APC~∆DPB    (AA similarity criteria)

ii)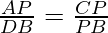 

AP*PB=CP*DP

Question 8. In Fig., two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that

(i) Δ PAC ~ Δ PDB

(ii) PA.PB = PC.PD

Solution:

i) In ∆PAC and ∆PDB,

∠P=∠P           ———[common]

∠1+∠2=180° ——–[linear pair angle]

∠2=180°+∠1

∠2+∠3=180° ——[sum of opposite angle of a cyclic quadrilateral is 180°]

∠3=180°-180°+∠1

∠3=∠1                   ————2

∠1=∠3 ———–[form 2]

∴∆APC~∆PDB        ———[AA similarity criteria]

ii)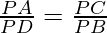

PA*PD = PC*PB

Question 9. In Fig., D is a point on side BC of ΔABC such that 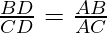. Prove that AD is the bisector of ∠BAC.

Solution:

Construction: Produce BA to E such that AE=AC join CE.

Proof: In ∆AEC, 

Since AE=AC

∴∠1=∠2             ——[Angle opposite to equal sides of ∆are=]

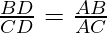
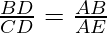        ———–(BY CONSTRUCTION)

By converse of BPT

AD||EC

And AC is a transversal then

∠3=∠1       ——-[corresponding angles]

∠4=∠2       ——-[alternate interior angles]

But ∠1=∠2      ——–[by construction]

∴AD bisects ∠BAC internally

Question 10. Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Fig.)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

Solution:

In ∆ABC,

AC is string

By Pythagoras theorem,

AC²=AB²+BC²

AC²=AB²+BC²

AC²=(1.8)²+(2.4)²

(AC)²=3.24+5.76

AC=√9

AC=3m

∴Length of string she have out=3m  

=5cm/sec*12sec

=60cm

=60/100 =0.6m  

AP=AC-0.6

=3-06

=2.4 m

Now in ∆ABP by Pythagoras theorem,

(AP)²=(AB)²+(PB)²

(2.4)²=(1.8)²+(PB)²

5.76=3.24 + (PB)²

5.76=3.24 + (PB)²

2.52=(PB)²

√2.52= PB

1.59=PB  

PD=PB+BD

PD=1.59+1.2

PD=2.79m  ———(approx)

Hence, the horizontal distance of the fly from nazima of the 12 sec in 2.79m.