Class 10 NCERT Solutions- Chapter 6 Triangles – Exercise 6.5 | Set 2

This exercise has been deleted as per new NCERT Syllabus

Chapter 6 Triangles – Exercise 6.5 | Set 1 

Question 11. An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after 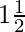hours?

Solution:

Distance covered by place left towards north = 1000 * 1.5

Distance covered by place left towards west = 1200 * 1.5 = 1800km

In right ∆ABC by Pythagoras theorem

(AC)² = (AB)² + (BC)²

(AC)² = (1500)² + (1800)²

= 250000 + 3240000

= 5490000

= √(3 * 3 * 61 * 10 * 10 * 10 * 10)

= 3 * 10 * 10√61

AC = 300√61

Distance between the two poles 300√61km

Question 12. Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.

Solution:

AB is pole of height = 11m

DC is another pole of height = 6m

BC = 12m

In fig.  DE = BC = 12m

AE = AB – EB

= 11 – 6

= 5m

In right ∆AED, by Pythagoras theorem

(AD)² = (AC)² + (DE)²

(AD)² = (5)² + (12)²

(AD)² = 25 + 144

AD = √169

AD = √(13 * 13)

AD = 13

Hence, the distance between the tops of the two poles is 13m.

Question 13. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE².

Solution:

To prove: (AE)² + (BD)² = (AB)² + (DE)²

Construction: Join AE, BD and DE

Proof:  

In ∆ACE, by Pythagoras theorem

(AE)² = (AC)² + (EC)²          -(1)

In ∆DCB, by Pythagoras theorem

(BD)² = (DC)² + (BC)²          -(2)

In ∆ACB, by Pythagoras theorem

(AB)² = (AC)² + (CB)²          -(3)

In ∆DCE, by Pythagoras theorem

(ED)² = (DC)² + (CE)²

Adding eq (1) and (2)

(AE)² + (BD)² = (AC)² + (EC)² + (DC)² + (DC)²

= (AC² + BC²) + (EC² + DC²)

= AB² + DE²          -(from 3 and 4)

Question 14. The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD (see Fig.). Prove that 2AB² = 2AC² + BC².

Solution:

Given: DB = 3CD

To prove: 2AB² = 2AC² + BC²

Proof: DB = 3CD

BC = CD + DB

BC = CD + 3CD

BC = 4CD

BC/4 = CD           -(1)

DB = 3(BC/4)           -(2)

In right ∆ADB, by Pythagoras theorem

AB² = AD² + DB²           -(3)

In right ∆ADC, by Pythagoras theorem

AC² = AD² + CD²           -(4)

Subtract eq(3) from (4)

AB² – AC² = AD² + DB² – (AD² + CD²)

= AD² + DB² + AD² – CD²

= DB² – CD²

= (3/4BC)² – (BC/4)²

= 9/6BC² – BC/16

= 8BC²/16

= AB² – AC² = BC²/2

2AB² – 2AC² = BC²

2AB² = 2AC² + BC²

Question 15.  In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3BC. Prove that 9AD² = 7AB².

Solution:

Prove that 9AD² = 7AB²

Construction: Join AD and draw AE perpendicular BC

Let each side, AB = AC = BC = a

BD = 1/3BC = 1/3a

BC = 1/2BC = 1/2a

DE = BE – BD

= 1/2a – 1/3a

= 3a – 2a/6

= DE = a/6

In right ∆AED, by Pythagoras theorem

AD² = AE² + DE²

AD² = (√3a/2)² + (a/6)²

= 3a²/4+ a²/36

= 27a²/36 + a²/36

AD² = 28a²/36

AD² = 7a²/9

9AD² = 7a²

9AD² = 7AB²

Question 16. In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.

Solution:

To prove: 3AB² = 4AD²

Proof: Let each side of one equilateral ∆ = a

BD = 1/2a          -[perpendicular bisects the side in on  an equilateral ∆]

In right ∆ADB, by Pythagoras theorem

(AB)²=(AD)² + (BD)²

(a)² = (AD)² + (1/2a)²

a² = AD² + (a/2)²

a² – a²/4 = AD²

3a²/4 = AD²

3a² = 4AD²

3AB² = 4AD²

Question 17. Tick the correct answer and justify: In ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm. The angle B is:

(A) 120°          (B) 60°

(C) 90°            (D) 45°

Solution:

(AC)² = (12)² = 144

(AB)² = (6√3)² = 6 * 6√3 = 36 * 3 = 108

(BC)² = (6)² = 36

(AB)² + (BC)² = 108 + 36 = 144

∴ It is right ∆ thus ∠B = 90°