Class 10 NCERT Solutions- Chapter 6 Triangles – Exercise 6.5 | Set 1

Question 1. Sides of triangles are given below. Determine which of them are right triangles? In the case of a right triangle, write the length of its hypotenuse.

(i) 7 cm, 24 cm, 25 cm

(ii) 3 cm, 8 cm, 6 cm

(iii) 50 cm, 80 cm, 100 cm

(iv) 13 cm, 12 cm, 5 cm

Solution:

(i) Given: 7cm, 24cm, 25cm

(25)²= 25 * 25 = 625

∴They are sides of a right ∆ and hypotenuse = 625  

(ii) Given: 3cm, 8cm, 6cm

(8)² = 8 * 8 = 64  

They are not side of right triangle.

(iii) Given: 50cm, 80cm, 100cm

(100)² = 100 * 100 = 10000

(50)² + (80)² = 2500 + 6400

Therefore, this is not right triangle.

(iv) Given: 13cm, 12cm, 5cm

(13)² = 13 * 13 = 169

(12)² + (5)² = 169

Therefore, this is the sides of right triangle and hypotenuse = 169

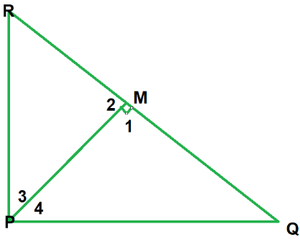
Question 2. PQR is a triangle right-angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM × MR.

Solution:

Given: A right ∆PQR right-angled at P and PM⊥QR

To show: PM² = QM * MR

PM * PM = QM * MR

In ∆PMQ and ∆PMR

∠1 =∠2           -(each 90°)

∠1 +∠2 +∠3 = 180°

90° + ∠4 + ∠5 = 180°

∠4 +∠5 = 180° – 90°

∠3 + ∠4 = 180° – 90°

∠4 +∠5 = ∠3 +∠4

∴∠5 =∠3  

∴∆PMQ ~ ∆RMP  

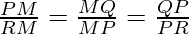
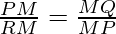
MP² = MQ.PM

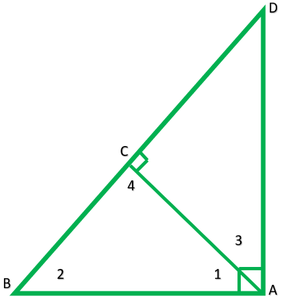
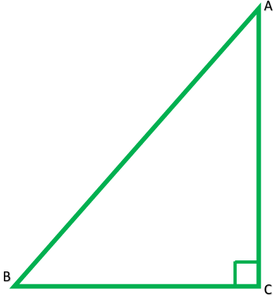
Question 3. In Fig., ABD is a triangle right angled at A and AC ⊥ BD. Show that

(i) AB² = BC × BD

(ii) AC² = BC × DC

(iii) AD² = BD × CD

Solution:

Given: A right ∆ABD, right angled at A and AC⊥ BD

To show:

(i)AB² = BC × BD

(ii) AC² = BC × DC

(iii) AD² = BD × CD

(i) AB² = BC × BD

AB * AB = BC.BD

In ∆ ABC and ∆ABD

∠B =∠B          -(common)

∠BCA = ∠A          -(each 90°)

∴ ∆ABC~∆DBA  

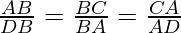
AB² = BC * DC

(ii) AC² = BC * DC

AC * AC = BC * DC

In ∆ABC and ∆ACD

∠ACB = ∠ACD          -(each 90°)

In ∆ ACB

∠1 + ∠2 + ∠3 = 180°

∠1 + ∠2 + 90° = 180°

∠1 + ∠2 = 90°           -(1)

∠1 + ∠3 = 90°          -(2)

∠1 + ∠2 =∠1 + ∠3

∴ ∠2 = ∠3  

∴ ∆ABC~∆DAC  

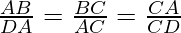
AC² = BC * CD

(iii) AD² = BD × CD

In ∆ABD and ∆ACD

∠A =∠ACD          -(each 90)

∠D =∠D          -(common)

∴ ∆ABD~∆CAD          -(AA similarity)  

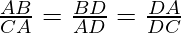
AD² = BD * CD

Question 4. ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².

Solution:

Given: ∆ABC right angled at B

To prove: AB² = 2AC²

According to Pythagoras theorem,

(AB)² = (AC)² + (BC)²

(AB)² = (AC)² + (AC)²           -(BC = AC)

AB² = 2AC²

Question 5. ABC is an isosceles triangle with AC = BC. If AB² = 2AC², prove that ABC is a right triangle.

Solution:

Given: ∆ABC is an isosceles triangle in which  

AC = BC

AB² = 2AC²

To prove: ABCD is right ∆  

AB² = 2AC²

AB² = AC² + AC²

∴ By the, converse of Pythagoras theorem ∆ACB is a right ∆ at C.  

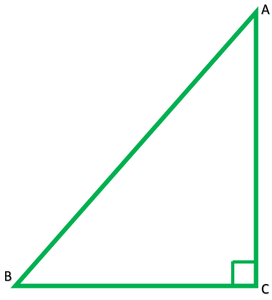
Question 6. ABC is an equilateral triangle of side 2a. Find each of its altitudes.

Solution:

Let ABC is an equilateral triangle of each 2a units

Construction: Draw AD ⊥ BC

In right ∆ ADB

(AB)² = (AD)² + (BD)²

(2a)² = (AD)² + (a)²

(4a)² = (AD)² + a²

4a² – a² = (AD)²

3a² = (AB)²

√3 a² = AD               ∴ Each of its altitude= √3 a unit

√3 a = AD  

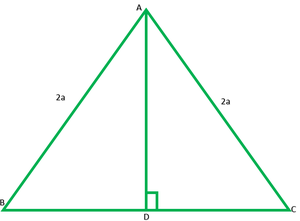
Question 7. Prove that the sum of the squares of the sides of the rhombus is equal to the sum of the squares of its diagonals.

Solution:

Given: ABCD is a rhombus

To prove: AB² + BC² + CD² + DA²

Proof: ABCD is rhombus and let diagonals AC and BD bisect each other at O.

∴ ∠AOB =∠BOC =∠COD =∠DOA = 90°  

In ∆AOB  

AB² = AC² + BO²

AB² = (1/2AC²) + (1/2BD²)

AB² = 1/4(AC² + BD²)

4AB² = AC² + BD²          -(1)

Similarly, in ∆BOC  

4BC² = AC² + BD²          -(2)

4CD² = AC² + BD²          -(3)

4AD² = AC² + BD²          -(4)

Adding 1, 2, 3, and 4

4AB² + 4BC² + 4CD² + 4DA² = 4(AC² + BD²)

4(AB² + BC² + CD² + DA²) = 4(AC² + BD²)

∴ AB² + BC² + CD² + DA² = AC² + BD² 

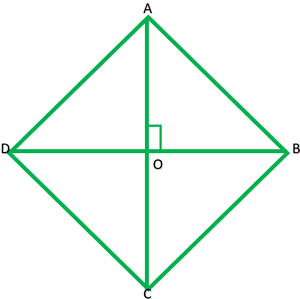
Question 8. In Fig. 6.54, O is a point in the interior of a triangle diagonals.

(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²

(ii) AF² + BD² + CE² = AE² + CD² + BF²

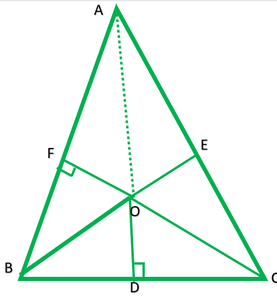
Solution: 

(i) In right ∆AFO, by Pythagoras theorem  

OA² = AP² + OF²          -(1)

In right ∆ODB, by Pythagoras theorem

OB² = BD² + OD²          -(2)

In right ∆OEC, by Pythagoras theorem

OC² = CE² + OE²          -(3)   

Adding 1, 2, and 3

OA² + OB² + OC² = AF² + BD² + CF² + OD² + OE²

OA² + OB² + OC² – OE² – OD² – OE² = AF² + BD² + CE²

(ii) AF² + BD² + CE² = AE² + CD² + BF²

OB² = BD² + OD²          -(1)

OC² = DC² + OD²          -(2)

Subtracting (1) from (2) we get,

OB² – OC² = BD² + OD² – (DC² + OD²)

= BD² + OD² – DC² – OD²

= BD² – DC²          -(3)

Similarly,  

OC² – AD² = CE² – EA²          -(4)

AO² = BO² = AF² – FB²          -(5)

Adding 3, 4, and 5, we get,

OB² – OC² + OC² – AO² + AO² – BO² = BD² – DC² + CE² – EA² + AF² – FB²

0 + DC² + EA² + FB² = BD² + CD² + AF²

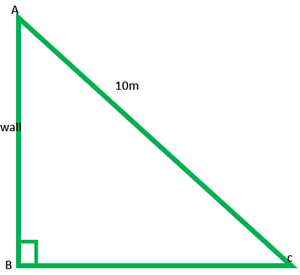
Question 9. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.

Solution:

AB is wall  = 8m

AC is ladder = 10m

BC = ?

In right ∆ABC, by Pythagoras theorem

(AC)² = (AB)² + (BC)²

(10)² = (8)² + (BC)²

100 = 64 + (BC)²

100 – 64 = (BC)²

36 = (BC)²

√36 = BC  

√(6 * 6) = BC

6 = BC  

Hence, the foot of the ladder is at a distance of 6 m from the base of the wall.

Question 10. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?

Solution:

In fig.  

AB is pole = 18m

AC is wire = 24m

BC = ?

In right ∆ABC, by Pythagoras theorem

(AC)² = (AB)² + (BC)²

(24)² = (18)² + (BC)²

576 = 324 + (BC)²

576 – 324 = (BC)²

252 = (BC)²

√252 = BC  

√(2 * 2 * 3 * 3 * 7) = BC 

2 * 3√7 = BC

6√7 = BC

∴ Hence, the stake may be placed at distance of 6√7 from the base of the pole.

Chapter 6 Triangles – Exercise 6.5 | Set 2