Calculation of Arithmetic Mean in Special Cases

A single value used to symbolise a whole set of data is called the Measure of Central Tendency. In comparison to other values, it is a typical value to which the majority of observations are closer. The arithmetic mean is one approach to measure central tendency in statistics. This measure of central tendency involves the condensation of a huge amount of data to a single value. 

For instance, the average weight of the 10 students in the class is 50 kg. However, one student weighs 28 kg, another student weighs 56 kg, and so on. This means that 50 kg is the one value that represents the average weight of the class and the value is closer to the majority of observations, which is called mean.

In real life, the importance of displaying a single value for a huge amount of data makes it simple to examine and analyse a set of data and deduce necessary information from it. The arithmetic mean is calculated by dividing the total value of all observations by the total number of observations. It is commonly referred to as Mean or Average by people in general and is commonly represented by the letter X̄.

Calculation of Arithmetic Mean in Special Cases

The calculation of the Mean varies under certain special cases such as:

1. Cumulative Series (Less than or More than):

Cumulative frequency distribution refers to data that is expressed as Less Than or More Than for all items in the series. Such cumulative frequency distribution needs to be changed into a simple frequency distribution so as to determine the arithmetic mean.

Example: 

Calculate the average marks using the following distribution of 60 students’ mathematics marks.

Solution:

To calculate the mean, first of all, change the given distribution into simple frequency distribution and find out the frequencies from the given cumulative frequencies. Then determine the mean of the series using any of the methods of calculating the mean in continuous series.

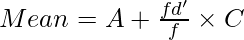
Mean = 51.3

2. Mid-Value Series:

The same method will be used to get the arithmetic mean as in the case of discrete series when mid-values are provided in the question of a continuous series (rather than class intervals).

Example:

Find out the mean of the following data:

Solution:

In the given example, the mid values are given. So the mean can be calculated using these mid values and there is no need to convert it into class intervals.

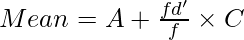
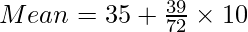
Mean = 40.41

3. Inclusive Series:

When presenting data as an inclusive series, there is no need to change the classes since the mid-value will stay consistent regardless of any adjustments made. There is no need to convert inclusive class intervals into exclusive classes. 

However, it is necessary to convert the inclusive series into the exclusive series if one needs to determine the median and mode.

Example: 

Find out the mean of the following data:

Solution:

In this given case, inclusive class intervals are not converted into exclusive class intervals to calculate the mean.

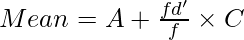
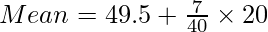
Mean = 53

4. Open-end Series:

Open-end class intervals are those without a lower limit for the first class interval and an upper limit for the last class interval. 

In this case, the mean cannot be determined without assuming the missing class limits. The pattern of class intervals in other classes affects the missing values. There may be some difficulty in determining the limits of the open-ended classes if the specified class intervals are not equal. In such cases, limits have to be assumed on some rational basis.

Example: 

Calculate the mean of the following data.

Solution:

In the above example, class intervals are uniform; i.e., there is a gap of 50 in each class interval. So, it can be assumed that open-end class intervals are also equivalent to 50. Thus, the lower limit of the first class interval is 0 (0-50) and the upper limit of the last class interval is 250 (200-250). The mean can now be calculated.

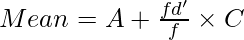
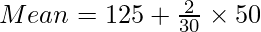
Mean = 128.33

5. Unequal Class-Intervals:

Sometimes the class intervals in the distribution may not be evenly distributed. After computing the mid-points of each interval, the mean can be calculated using any of the methods of calculating the mean. It implies that class intervals are not made equal.

Example: 

Calculate the mean of the following data.

Solution:

The mean can be calculated directly without making any change in the above class intervals.

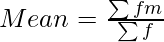
Mean = 47