Mean Deviation: Coefficient of Mean Deviation, Merits, and Demerits
Last Updated :
06 Nov, 2023
Range, Interquartile range, and Quartile deviation all have the same defect; i.e., they are determined by considering only two values of a series: either the extreme values (as in range) or the values of the quartiles (as in quartile deviation). This approach of analysing dispersion by determining the location of limits is also known as the Limits Approach because it does not consider all the items in the series. Therefore, it is always preferable to have a measure of dispersion that accounts for all of a series’ observations and is calculated in relation to a central value. If the variations of items are derived from an average, then such a measure of dispersion could throw light on the creation of the series and the dispersal of items around a central value. One such measure of dispersion is Mean Deviation.
What is Mean Deviation?
The arithmetic average of the deviations of various items from a measure of central tendency (mean, median, or mode) is known as the Mean Deviation of a series. Other names for Mean Deviation are the First Moment of Dispersion and Average Deviation.
Mean deviation is calculated by using all of the items in the series. It can theoretically be calculated by taking deviations from any of the three averages. However, in reality, either the mean or the median is used to determine the mean deviation. Mode is usually not considered because its value is uncertain and provides incorrect results. Since the sum of deviations from the median is less than the sum of deviations from the mean, the former is considered better than the latter.
Note: The sign (+ or -) of deviations is ignored while calculating deviations from the selected average, assuming all deviations are positive.
Coefficient of Mean Deviation
Mean Deviation is an absolute measure of dispersion. In order to convert it into a relative measure, it is divided by the average from which it has been calculated. It is known as the Coefficient of Mean Deviation.
Coefficient of Mean Deviation from Mean (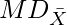 ) =
) = 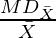
Coefficient of Mean Deviation from Median ( ) =
) = 
The mean deviation can be calculated using the mean, median and mode. The formula for calculating are:
To calculate the mean, first add up all of the observations and then, divide the total by the number of observations. The following are formulas for mean deviation about the mean in different statistical series:
In case of Individual Series:
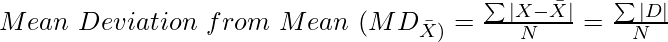
Where,
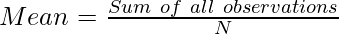
In case of Discrete Series:
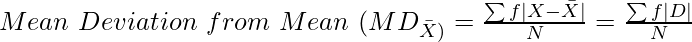
Where,

In case of Continuous Series:
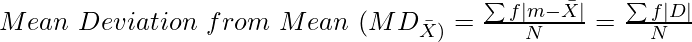
Where,
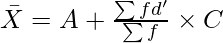
X̄ = Arithmetic Mean; A = Assumed Mean; d = m – A; i.e., deviations of mid-points from assumed mean; d’= Step Deviations (deviations divided by common factor); Σfd’ = Sum of product of step deviations (d’) with their respective frequencies (f); C = Common Factor; Σf =Total number of items.
The value that divides the data into its upper and lower half is called the median. The number in the middle of an arranged set of values, either ascending or descending, is called the median. The following are formulas for mean deviation about the median:
In case of Individual Series:
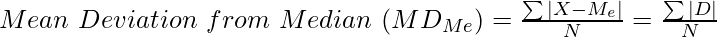
Where,
In case n is odd; ![Rendered by QuickLaTeX.com Me=Size~of~[\frac{N+1}{2}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ddb5ca9d887a26fcb5d5c2bca24bab1c_l3.png)
In case n is even; ![Rendered by QuickLaTeX.com Me=Size~of~[\frac{N}{2}]^{th}~item+[\frac{N+1}{2}]^{th}~item/2](https://quicklatex.com/cache3/db/ql_5aebf0f4bc15de37f580a529e16000db_l3.png)
In case of Discrete Series:
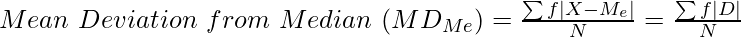
Where,
In case n is odd; ![Rendered by QuickLaTeX.com Me=Size~of~[\frac{N+1}{2}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ddb5ca9d887a26fcb5d5c2bca24bab1c_l3.png)
In case n is even; ![Rendered by QuickLaTeX.com Me=Size~of~[\frac{N}{2}]^{th}~item+[\frac{N+1}{2}]^{th}~item/2](https://quicklatex.com/cache3/db/ql_5aebf0f4bc15de37f580a529e16000db_l3.png)
In case of Continuous Series:
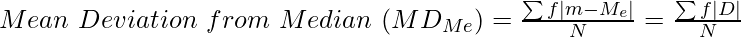
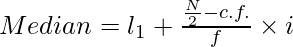
Where,
l1 = lower limit of the median class, c.f. = cumulative frequency of the class preceding the median class, f = simple frequency of the median class, i = class size of the median group or class.
(III) Mean Deviation from the Mode
The observation that occurs at the maximum time or with the highest frequency in the given set of data is called the mode, or modal value. A set of numbers or data that has only one mode is referred to as unimodal, two modes are referred to as bimodal, and three modes are referred to as trimodal. On the other hand, a multimodal set of numbers is any set that has four or more modes. The following formulas can be used to get the mean deviation about the mode:
In case of Individual Series:

Where, mode is the value that appears the most frequently in the data set.
In case of Discrete Series:

Where, mode is the value that appears the most frequently in the data set.
In Case of Continuous series


Where,
Mo = Mode, l1 = Lower limit of modal class, f1 = Frequency of modal class, f0 = Frequency of class preceding the modal class, f2 = Frequency of the class succeeding the modal class, i = Class interval of the modal class
Merits of Mean Deviation
1. Simplicity: The calculation is simple and easy to understand.
2. Based on all observations: Since mean deviation is based on every item in the series, it provides a more thorough estimate of dispersion than quartile deviation and range.
3. Less impact from extreme values: It is less impacted by extreme observations when compared to standard deviation.
4. Rigidly specified: The mean deviation has an exact and distinct value, and it is rigidly defined.
Demerits of Mean Deviation
1. Unable to be treated algebraically: The mean deviation ignores both positive and negative deviation signs. Therefore, this approach cannot be applied to further algebraic treatment.
2. Not well defined: Since deviations can be derived from any central tendency measure and the mean deviation obtained from various averages (mean, median, and mode) will change, the dispersion needs to be better defined.
3. Unsuitable for open-end classes: It is impossible to calculate the mean deviation for a distribution using an open-end class.
4. Less reliable: Since mode frequently has no stable value, calculating the mean deviation from mode is unreliable.
5. Difficult computations: The mean deviation calculation gets challenging if the mean, mode, and median are in fractions.
Share your thoughts in the comments
Please Login to comment...