Calculation of Mean in Continuous Series | Formula of Mean
Last Updated :
07 Aug, 2023
What is Mean?
Mean is the sum of a set of numbers divided by the total number of values. It is also referred to as the average. For instance, if there are four items in a series, i.e. 2, 5, 8, 3, and 9. The simple arithmetic mean is (2 + 5 + 8 + 3 + 9) / 5 = 5.4.
What is Continuous Series?
In continuous series (grouped frequency distribution), the value of a variable is grouped into several class intervals (such as 0-5,5-10,10-15) along with the corresponding frequencies. The method used to determine the arithmetic average in a continuous series is the same as that used in discrete series. The midpoints of several class intervals replace the class interval in a continuous series. When it is done, a continuous series and a discrete series are the same.
Example of Continuous Series
If 15 students of a class score marks between 50-60, 10 students score marks between 60-70, and 20 students score marks between 70-80, then this information will be shown as:
Mean in Continuous Series
The arithmetic mean in continuous series can be calculated by using:
- Direct Method;
- Shortcut Method; and
- Step Deviation Method
Example 1:
Calculate the mean of the following data using Direct Method and Short-Cut Method:
Solution:
Direct Method:
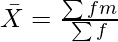
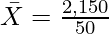
Mean  = 43
= 43
Short-Cut Method:
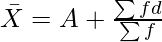
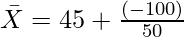
Mean  = 43
= 43
Example 2:
Find the missing frequency of the following series if the average marks is 30.5:
Solution:
Let us assume that the missing frequency is f.
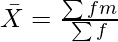
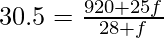
854 + 30.5f = 920 + 25f
5.5f = 66
f = 12
Missing Frequency (f) = 12
Example 3:
Calculate average profit earned by 50 companies from the following data using Step Deviation Method:
Solution:
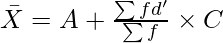
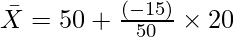
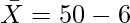
Average Profit  = ₹44 Crores
= ₹44 Crores
Share your thoughts in the comments
Please Login to comment...