Weighted Arithmetic Mean
Last Updated :
06 Apr, 2023
Simple Arithmetic Mean gives equal importance to all the variables in a series. However, in some situations, a greater emphasis is given to one item and less to others, i.e., ranking of the variables is done according to their significance in that situation. For example, during inflation, the price of everything in an economy tends to rise, but households pay more importance to the rise in the price of necessary food items rather than the rise in the price of clothes. In other words, more significance is given to the price of food and less to the price of clothes. This is when Weighted Arithmetic Mean comes into the picture.
When every item in a series is assigned some weight according to its significance, the average of such series is called Weighted Arithmetic Mean.
Here, weight stands for the relative importance of the different variables. In simple words, the Weighted Arithmetic Mean is the mean of weighted items and is also known as the Weighted Average Mean.
Calculation of Weighted Arithmetic Mean
Weighted Arithmetic Mean is calculated as the weighted sum of the items divided by the sum of the weights.
Steps to calculate Weighted Arithmetic Mean:
- Step-1: All the items (X) in a series are weighted according to their significance. Weights are denoted as ‘W’.
- Step-2::Add up all the values of weights ‘W’ to get the sum total of weights, i.e.,
∑W= W1+W2+W3+…………+Wn
- Step-3:Items (X) are multiplied by the corresponding weights (W) to get ‘XW’.
- Step-4:Add up all the values of ‘XW’ to get the sum total of the product ‘XW’, i.e.,
∑XW= X1W1+X2W2+X3W3+…………..+XnWn
- Step-5: To get the weighted mean, divide the weighted sum of the items ‘∑XW’ by the sum of weights ‘∑W’.
Formula for calculating Weighted Arithmetic Mean is
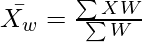
Example:
Calculate a weighted mean of the following data:
| Items (X) | 5 | 10 | 25 | 20 | 25 | 30 |
| Weight (W) | 8 | 4 | 5 | 10 | 7 | 6 |
Solution:
| Items (X) | Weight (W) | XW |
| 5 | 8 | 40 |
| 10 | 4 | 40 |
| 25 | 5 | 125 |
| 20 | 10 | 200 |
| 25 | 7 | 175 |
| 30 | 6 | 180 |
| | ∑W=40 | ∑XW=760 |
Weighted Mean =
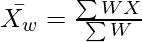
= 760/40
= 19
Explanation:
- Multiply each item with its corresponding weight to get XW, i.e.,
[ 5×8=40, 10×4=40, 25×5=125, 20×10=200, 25×7=175, 30×6=180 ]
- Add up all the values of weight to get the sum of weights, i.e.,
∑W= 8 + 4 + 5 + 10 + 7 + 6 = 40
- Add up all the values of the product of weight and items(XW) to get the sum of the product, i.e.,
∑XW= 40 + 40 + 125 + 200 + 175 + 180 = 760
- Divide ∑XW by ∑W to get the weighted arithmetic mean, i.e., 19.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...