Arithmetic Mean: Meaning, Example, Types, Merits, and Demerits

A single value used to symbolise a whole set of data is called the Measure of Central Tendency. In comparison to other values, it is a typical value to which the majority of observations are closer. The arithmetic mean is one approach to measure central tendency in statistics. This measure of central tendency involves the condensation of a huge amount of data to a single value. For instance, the average weight of the 20 students in the class is 50 kg. However, one student weighs 48 kg, another student weighs 53 kg, and so on. This means that 50 kg is the one value that represents the average weight of the class and the value is closer to the majority of observations, which is called mean. In real life, the importance of displaying a single value for a huge amount of data makes it simple to examine and analyse a set of data and deduce necessary information from it.

Meaning of Arithmetic Mean

The arithmetic mean is calculated by dividing the total value of all observations by the total number of observations. It is commonly referred to as Mean or Average by people in general and is commonly represented by the letter X̄.

Types of Arithmetic Mean

There are two methods for calculating the arithmetic mean:

1. Simple Arithmetic Mean, and

2. Weighted Arithmetic Mean.

1. Simple Arithmetic Mean

The sum of a set of numbers divided by the total number of values in the set leads to a simple arithmetic mean. It is also referred to as the average. For instance, if there are four items in a series, i.e. 6, 7, 8, and 9. The simple arithmetic mean is (6 + 7 + 8 + 9) / 4 = 7.5.

2. Weighted Arithmetic Mean

The term weighted mean refers to the average when different items in the series are assigned different weights based on their corresponding importance.

While calculating the simple arithmetic mean, it is assumed that each item in the series has equal importance. There are; however, certain cases in which the values of the series observations are not equally important. A simple arithmetic mean will not accurately represent the provided data if all the items are not equally important. Thus, assigning weights to the different items becomes necessary. Different items are assigned different weights based on their relative value. In other words, items that are more significant are given greater weights.

Properties of Arithmetic Mean

Some of the properties of Arithmetic Mean are as follows:

1. The sum of deviations of the observations from their arithmetic mean is always zero : Arithmetic Mean is a point of balance. It means that the sum of positive deviations from mean and the sum of negative deviations from mean are equal. Because of this, the sum of deviations of the observations from their arithmetic mean is always zero. 

Example:

2. The sum of the square of the deviations of the items from their arithmetic mean is minimum : The sum of the square of the deviations of the items from their arithmetic mean is less than the sum of the square of deviations from any other value.

Example:

3. If each observation of a series is increased or decreased by a constant, then the arithmetic mean of the new series will also get increased or decreased by that constant respectively: For instance, the arithmetic mean of the series 4, 6, 2, 8, 10 is 6. If 2 is added to each item of the series, then the mean of the new series 6, 8, 4, 10, 12 will also get increased by 2; i.e., the new arithmetic mean will be 8.

4. If each observation of a series is multiplied or divided by a constant, then the arithmetic mean of the new series will also get multiplied or divided by that constant respectively: For instance, the arithmetic mean of the series 4, 6, 2, 8, 10 is 6. If 2 is divided by each of the items of the series, the mean of the new series 2, 3, 1, 4, 5 will also get divided by 2; i.e., the new arithmetic mean will be 3.

5. Mean of the Combined Series: If the arithmetic mean of two or more related series is given, then it is possible to calculate the combined arithmetic mean of the series as a whole. 

6. If any two values out of arithmetic mean, number of items, or a total of the values are known, then it is possible to calculate the third value: The missing items, missing frequency, or correct mean can be determined with the help of the following formulas:

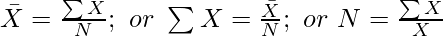
Merits of Arithmetic Mean

Arithmetic mean is the most commonly employed measure of central tendency in practice because of the following merits:

1. Simple to Understand and Easy to Calculate: The calculation of the arithmetic mean necessitates a basic knowledge of addition, multiplication, and division of numbers. Therefore, even a layman with elementary knowledge can calculate the arithmetic mean. Besides, with the arithmetic mean, it becomes very easy to figure out the value per item or cost per unit, etc. 

2. Certainty: An algebraic formula defines the arithmetic mean. Thus, everyone who calculates the average gets the same answer, which ultimately eliminates the chance for deliberate prejudice or personal bias.

3. Based on all Items: The arithmetic mean is calculated by considering all the values. Consequently, it is regarded as being more representative of the distribution.

4. Least affected by Fluctuations in Sample: The arithmetic mean is the least impacted by sampling fluctuations when compared with all other averages. The arithmetic mean provides a suitable basis for comparison in case the number of items in a series is large because abnormalities (errors) in one direction are offset by abnormalities in the other. As a result, the arithmetic mean is considered to be a stable measure.

5. Convenient Method of Comparison: Arithmetic Average provides a simple way to compare two or more distributions. For this reason, it is a convenient method for comparison.

6. Algebraic Treatment: Arithmetic mean can be algebraically treated further. It is commonly employed in the computation of several other statistical measures such as mean deviation, standard deviation, etc., as it can be treated mathematically.

7. No Arrangement Required: The calculation of the arithmetic mean does not require the grouping or arranging of the items. For example, in the case of median, the values must be first placed in ascending or descending order, only then the calculation can be done.

Demerits of Arithmetic Mean

Arithmetic mean matches the majority of the properties for a perfect average, but it has some demerits and needs to be used carefully. Some demerits of arithmetic mean are:

1. Affected by Extreme Values: Extreme values have an undue influence on the arithmetic average because it is calculated from all the values in the series, whether they are very small or very large.

2. Assumption in the case of Open-end Classes: It is impossible in the case of open-end classes to calculate the arithmetic mean without making an assumption about the magnitude of the class.

3. Absurd Results: Arithmetic mean can sometimes provide results that appear absurd. For instance, if the average number of students (in the school) in a particular class and a particular section comes out to be 15.6, then obviously the result (average) is absurd as children cannot be divided into fractions.

4. Not Possible in the case of Qualitative Characteristics: Arithmetic mean cannot be computed for qualitative data, such as data on IQ, beauty, honesty, etc. The only appropriate average, in this case, is the median.

5. More Stress on Items of Higher Value: The arithmetic mean places more emphasis on higher items in a series than it does on lower items. This means that it has an upward bias. If three out of four items have small values and one is quite big, the average will be significantly increased by the big value. However, the opposite is untrue. If a series of four items consists of three items with large values and one item with a small value, the arithmetic average will not be significantly decreased.

6. Complete Data Required: Without all the items in a series, it is impossible to calculate the arithmetic mean. For instance, if the values of 99 out of 100 items are known, then the arithmetic average cannot be determined. However, the median and mode averages do not require complete data.

7. Calculation by Observation is not Possible: Arithmetic mean cannot be estimated by simply observing a series, just like in the case of median or mode.

8. No Graph Use: Graphs cannot be used to calculate the arithmetic mean.

9. Non-existent Value as Mean: An arithmetic average might sometimes be a fictional figure that does not exist in the series. 10, 12, 19, and 27 have an arithmetic average of 17. But there is no item in the series that has a value of 17.