Types of Angles: An angle is a geometric figure formed by two rays meeting at a common endpoint. It is measured in degrees or radians. It deals with the relationship of points, lines, angles, and shapes in space. Understanding different types of angles is crucial for solving theoretical problems in geometry.

Types of Angles
As we know an angle is a geometrical shape formed by joining two rays at their endpoints and is generally measured in degrees. There are different types of angles in geometry which are mentioned in the article below. We have mentioned various types of angles with diagrams, definitions, and examples below.
What are Angles?
Angles are a mathematical concept used to measure the number of turns between two lines or line segments that meet at a common point. They are typically measured in degrees or radians, and are often represented by the symbol “θ”. In Euclidean geometry, an angle is defined as a figure that is formed by two rays (by their intersection).
The rays are known as the sides of the angle and the common point shared by the two rays is known as the vertex of the angle. Angle tells about the rotation and the amount of rotation of a certain parameter. Therefore, in physics, angular displacement and the terms used in the rotation part are concerned with angles.
How many Types of Angles are there?
There are various types of angles based on different classifications. The most basic classification is measurement. There are 6 types of angles based on measurement – Acute Angle, Right Angle, Obtuse Angle, Straight Angle, Reflex Angle, and Complete Angle. Other than that, There are positive angles and negative angles.
Read More
Here are the types of angles based on different classifications:
Types of Angles Based on Measurement
Measurement of angles is useful to differentiate types of angles. Based on their measurement, there are six different types of Angles commonly used in Mathematics:
- Acute Angle – Less than 90° at the Vertex
- Right Angle – between 90° and 180°.
- Obtuse Angle – Exactly 90° at the Vertex
- Straight Angle – Exactly 180°
- Reflex Angle – between 180°- 360°
- Complete Angle – 360°
Below is an explanation of each of the different types of angles with their figures:
Acute Angle
When the two rays make any inclination between zero to ninety degrees it is called an Acute angle i.e. 0° < Angle < 90°. The corners of an acute angle triangle, the tip of a pencil, or the point of a star are some examples of acute angles. Here, the angle given below is acute.

Acute Angle Diagram
Read More
Right Angle
When the two rays make any inclination of exactly nighty degrees it is called a Right angle i.e. Angle = 90°. You can find it in many everyday objects, like the corners of a book or the edge of a door frame. Here, the angle given below is a right angle.

Right Angle Diagram
Also Read
Obtuse Angle
When the two rays make any inclination of exactly nighty degrees it is called an Obtuse angle i.e. 90° < Angle < 180°. The largest angle of the obtuse angle tangle is a key example of the obtuse angles. Here, the angle given below is a right angle.

Obtuse Angle Diagram
Read More
Straight Angle
When the two rays make any inclination of exactly 180 degrees it is called a Straight angle i.e. Angle = 180°. A straight angle is used to straight edge which is used to align something parallel to the horizontal. Here, the angle given below is a straight angle.

Straight Angle Diagram
Also Read
Reflex Angle
When the two rays make any inclination of greater than 180 degrees but less than 270 degrees. It is called a reflexive angle i.e. 180° < Angle < 270°. The exterior angle of any basic regular polygon is a reflex angle. Here, the angle given below is a reflexive angle.
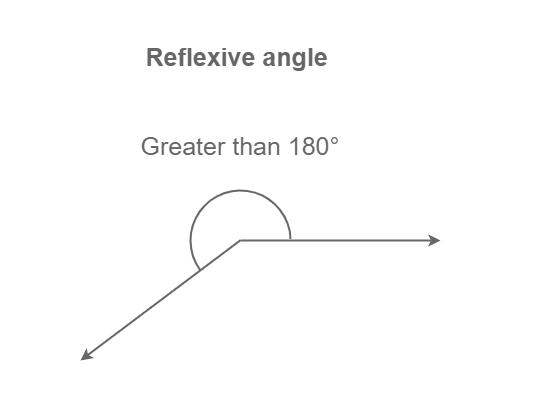
Reflex Angle Diagram
Also Read
Complete Angle
When the two rays make any inclination of 360° i.e. they overlap each other. It is called a complete angle i.e. Angle = 360°. Here, the angle given below is a complete angle.

Complete Angle Diagram
Also Read
Types of Angles based on Rotation
On the basis of measurement of rotation, Angle can be two types:
- Positive Angles
- Negative Angles
Positive Angles
Angles that are measured in a counterclockwise direction from the base are called Positive angles. Generally, positive angles are used to represent angles in geometry. From the origin, if an angle is drawn in the First Quadrant, it forms a positive angle.
Negative Angles
Angles that are measured in a clockwise direction from the base are called Negative angles. From the origin, if an angle is drawn in the Third Quadrant, it forms a negative angle.

Positive and Negative Angle
Types of Pair of Angles
Based on the sum of pairs, two angles pairs can be classified as
- Adjacent Angles
- Linear Pair
- Vertically Opposite Angles
- Complementary Angles
- Supplementary Angles
Adjacent Angles
Two angles are called adjacent angles if they share only one common arm. In other words, adjacent angles are those two angles that have a common vertex and a common side but no common interior points. The sum of adjacent angles is equal to the measure of the larger angle formed by the two adjacent angles.

Adjacent Angles Diagram
Read
Linear Pair
A linear pair refers to a pair of adjacent angles whose non-common sides are opposite rays. In other words, two angles are said to form a linear pair if their sum is equal to 180°. For example, angles 70° and 110° form a linear pair because they are adjacent angles (share a common vertex and side) and their non-common sides form a straight line.

Linear Pair of angles
Must Read
Vertically Opposite Angles
Vertically opposite angles are a pair of angles formed when two lines intersect. These angles have the same measure, and their opposite rays form a straight line. Vertically opposite angles are always congruent, and the measure of one angle can be used to find the measure of the other angle.

Read More
Complementary Angles
If the sum of two angles is equal to 90°, they are termed complementary angles. Two angles are complementary if they sum up to 90°. For example, 40° and 50° are complementary angles as 40° + 50° = 90°. Here, one angle complements the other angle.
Supplementary Angles
If the sum of two angles is equal to 180°, they are termed supplementary angles. Two angles are supplementary if they sum up to 90°. For example, 140° and 40° are supplementary angles as 140° + 40° = 180°. Here, one angle supplements the other angle.
Parts of an Angle
The two main parts related to an angle are – the arms and the vertex.

Parts of an Angle
Arms of the Angle: The two rays which join at a common point to form the angle are called the arms of the angle. Observe the figure above which shows that OA and OB are the arms of the angle AOB.
Vertex of the Angle: Vertex is a common endpoint that is shared by the two rays. Observe the figure in which the vertex O is marked as the joining point of the two arms.
People Also View
Solved Examples on Types of Angles
Example 1: An Angle A measures 135° in measure. Which type of category does Angle A fall into?
Answer:
Angle A lies between 90° to 180° in measure. Angle A is, therefore, an Obtuse Angle.
Example 2: An Angle S measures 35° in measure. Which type of category does Angle S fall into?
Answer:
Angle S lies between 0° to 90° in measure. Angle S is therefore an Acute Angle.
Example 3: An Angle X measures 235 degrees in measure. Which type of category does Angle X fall into?
Answer:
Angle X lies between 180° to 360° in measure. Angle X is therefore a Reflex Angle.
Example 4: An Angle Z measures 335° in measure. Which type of category does Angle Z fall into?
Answer:
Angle Z lies between 180° to 360° in measure. Angle Z is therefore a Reflex Angle.
Example 5: Find the complement of 40° and the supplement of 25°.
Solution:
Those angles that sum up to 90°are called as Complementary angles .
The complement of 40° is 50° because (90° – 40° = 50°).
Those angles that sum up to 180°are called as Supplementary angles.
The supplement of 25° is 155° because (180° – 25° = 155°).
Practice Problems on Types of Angles
1. Identify the type of angle that measures exactly 90 degrees.
Options: A) Acute B) Right C) Obtuse D) Reflex
2. Which type of angle measures more than 180 degrees but less than 360 degrees?
Options: A) Acute B) Right C) Reflex D) Straight
3. If an angle measures 35 degrees, what type of angle is it?
Options: A) Acute B) Right C) Obtuse D) Reflex
4. Which angle is formed by the hands of a clock at 6:00?
Options: A) Acute B) Right C) Obtuse D) Straight
5. A skateboard ramp forms an angle of 175 degrees where it meets the ground. What type of angle is this?
Options: A) Acute B) Right C) Obtuse D) Reflex
Types of Angles – FAQs
What is an Angle?
Figure formed by two rays and a point in geometry is called an angle, where rays are called arms of angle and the point is called vertex of angle.
What are the Types of Angles Based on Rotation?
On the basis of rotation, types of angles are classified into:
- Positive Angles
- Negative Angles
What are the Six Different Types of Angles Used in Geometry?
The six different angles used in geometry are:
- Acute Angle
- Obtuse Angle
- Right Angle
- Straight Angle
- Reflex Angle
- Complete Angle
What are the Types of Triangles on the Basis of Angles?
On the basis of angles, Triangles are classified as:
- Acute Angled Triangle
- Obtuse Angled Triangle
- Right Angled Triangle
What is an Acute Angle?
An acute angle is an angle that measures between 0 and 90 degrees.
What is a Right Angle?
A right angle is an angle that measures exactly 90 degrees.
What is an Obtuse Angle?
An obtuse angle is an angle that measures between 90 and 180 degrees.
What is a Reflex Angle?
A reflex angle is an angle that measures between 180 and 360 degrees.
What is Straight Angle?
A straight angle is an angle that measures exactly 180 degrees.
What are Complementary and Supplementary angles?
If two angles add up to 90°, they are termed complementary angles. For example, 40°, and 50° are complementary angles because their sum is 90°. If two angles add up to 180°, they are termed supplementary angles. For example, 95° and 85° are supplementary because their sum is 180°.
Share your thoughts in the comments
Please Login to comment...