Sort an array when two halves are sorted
Last Updated :
23 Jun, 2023
Given an integer array of which both first half and second half are sorted. Task is to merge two sorted halves of array into single sorted array.
Examples:
Input : A[] = { 2, 3, 8, -1, 7, 10 }
Output : -1, 2, 3, 7, 8, 10
Input : A[] = {-4, 6, 9, -1, 3 }
Output : -4, -1, 3, 6, 9
Method 1: A Simple Solution is to sort the array using built in functions (generally an implementation of quick sort).
Below is the implementation of above method:
C++
#include <bits/stdc++.h>
using namespace std;
void mergeTwoHalf(int A[], int n)
{
sort(A, A + n);
}
int main()
{
int A[] = { 2, 3, 8, -1, 7, 10 };
int n = sizeof(A) / sizeof(A[0]);
mergeTwoHalf(A, n);
for (int i = 0; i < n; i++)
cout << A[i] << " ";
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static void mergeTwoHalf(int[] A, int n)
{
Arrays.sort(A);
}
static public void main(String[] args)
{
int[] A = { 2, 3, 8, -1, 7, 10 };
int n = A.length;
mergeTwoHalf(A, n);
for (int i = 0; i < n; i++)
System.out.print(A[i] + " ");
}
}
|
Python3
def mergeTwoHalf(A, n):
A.sort()
if __name__ == '__main__':
A = [2, 3, 8, -1, 7, 10]
n = len(A)
mergeTwoHalf(A, n)
for i in range(n):
print(A[i], end=" ")
|
C#
using System;
class GFG {
static void mergeTwoHalf(int[] A, int n)
{
Array.Sort(A);
}
static public void Main()
{
int[] A = { 2, 3, 8, -1, 7, 10 };
int n = A.Length;
mergeTwoHalf(A, n);
for (int i = 0; i < n; i++)
Console.Write(A[i] + " ");
}
}
|
PHP
<?php
function mergeTwoHalf(&$A, $n)
{
sort($A, 0);
}
$A = array(2, 3, 8, -1, 7, 10);
$n = sizeof($A);
mergeTwoHalf($A, $n);
for ($i = 0; $i < $n; $i++)
echo $A[$i] . " ";
?>
|
Javascript
<script>
function mergeTwoHalf(A, n)
{
A.sort((a,b) => a-b);
}
var A = [ 2, 3, 8, -1, 7, 10 ];
var n = A.length;
mergeTwoHalf(A, n);
for (var i = 0; i < n; i++)
document.write( A[i] + " ");
</script>
|
Time Complexity: 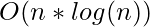 best & average case,
best & average case, 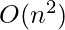 worst case (for quicksort)
worst case (for quicksort)
Space Complexity: 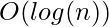 to
to 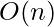 depending on the case & implementation (for quicksort)
depending on the case & implementation (for quicksort)
For more details, check out the GFG article on Quicksort.
Method 2: A more efficient solution is to use an auxiliary array which is very similar to the Merge Function of Merge sort.
Below is the implementation of above approach :
C++
#include <bits/stdc++.h>
using namespace std;
void mergeTwoHalf(int A[], int n)
{
int half_i = 0;
int temp[n];
for (int i = 0; i < n - 1; i++) {
if (A[i] > A[i + 1]) {
half_i = i + 1;
break;
}
}
if (half_i == 0)
return;
int i = 0, j = half_i, k = 0;
while (i < half_i && j < n) {
if (A[i] < A[j])
temp[k++] = A[i++];
else
temp[k++] = A[j++];
}
while (i < half_i)
temp[k++] = A[i++];
while (j < n)
temp[k++] = A[j++];
for (int i = 0; i < n; i++)
A[i] = temp[i];
}
int main()
{
int A[] = { 2, 3, 8, -1, 7, 10 };
int n = sizeof(A) / sizeof(A[0]);
mergeTwoHalf(A, n);
for (int i = 0; i < n; i++)
cout << A[i] << " ";
return 0;
}
|
Java
import java.io.*;
class GFG {
static void mergeTwoHalf(int[] A, int n)
{
int half_i = 0;
int i;
int[] temp = new int[n];
for (i = 0; i < n - 1; i++) {
if (A[i] > A[i + 1]) {
half_i = i + 1;
break;
}
}
if (half_i == 0)
return;
i = 0;
int j = half_i;
int k = 0;
while (i < half_i && j < n) {
if (A[i] < A[j])
temp[k++] = A[i++];
else
temp[k++] = A[j++];
}
while (i < half_i)
temp[k++] = A[i++];
while (j < n)
temp[k++] = A[j++];
for (i = 0; i < n; i++)
A[i] = temp[i];
}
static public void main(String[] args)
{
int[] A = { 2, 3, 8, -1, 7, 10 };
int n = A.length;
mergeTwoHalf(A, n);
for (int i = 0; i < n; i++)
System.out.print(A[i] + " ");
}
}
|
Python3
def mergeTwoHalf(A, n):
half_i = 0
temp = [0 for i in range(n)]
for i in range(n - 1):
if (A[i] > A[i + 1]):
half_i = i + 1
break
if (half_i == 0):
return
i = 0
j = half_i
k = 0
while (i < half_i and j < n):
if (A[i] < A[j]):
temp[k] = A[i]
k += 1
i += 1
else:
temp[k] = A[j]
k += 1
j += 1
while i < half_i:
temp[k] = A[i]
k += 1
i += 1
while (j < n):
temp[k] = A[j]
k += 1
j += 1
for i in range(n):
A[i] = temp[i]
A = [ 2, 3, 8, -1, 7, 10 ]
n = len(A)
mergeTwoHalf(A, n)
print(*A, sep = ' ')
|
C#
using System
class GFG {
static void mergeTwoHalf(int[] A, int n)
{
int half_i = 0
int i
int[] temp
= new int[n]
for (i = 0 i < n - 1 i++)
{
if (A[i] > A[i + 1]) {
half_i = i + 1 break
}
}
if (half_i == 0)
return
i = 0 int j = half_i int k
= 0 while (i < half_i & &j < n)
{
if (A[i] < A[j])
temp[k++] = A[i++] else temp[k++]
= A[j++]
}
while (i < half_i)
temp[k++] = A[i++]
while (j < n) temp[k++]
= A[j++]
for (i = 0 i < n i++) A[i]
= temp[i]
}
static public void Main()
{
int[] A
= { 2,
3,
8,
-1,
7,
10 } int n
= A.Length mergeTwoHalf(A, n)
for (int i = 0 i < n i++)
Console.Write(A[i] + " ")
}
}
|
Javascript
<script>
function mergeTwoHalf(A, n)
{
let half_i = 0;
let temp = new Array(n);
temp.fill(0);
for (let i = 0; i < n - 1; i++) {
if (A[i] > A[i + 1]) {
half_i = i + 1;
break;
}
}
if (half_i == 0)
return;
let i = 0, j = half_i, k = 0;
while (i < half_i && j < n) {
if (A[i] < A[j])
temp[k++] = A[i++];
else
temp[k++] = A[j++];
}
while (i < half_i)
temp[k++] = A[i++];
while (j < n)
temp[k++] = A[j++];
for (let i = 0; i < n; i++)
A[i] = temp[i];
}
let A = [ 2, 3, 8, -1, 7, 10 ];
let n = A.length;
mergeTwoHalf(A, n);
for (let i = 0; i < n; i++)
document.write(A[i] + " ");
</script>
|
Time Complexity: 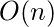
Space Complexity: 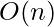
Reference: https://www.careercup.com/question?id=8412257
Share your thoughts in the comments
Please Login to comment...