Quartile Deviation in Continuous Series | Formula, Calculation and Examples

Last Updated : 13 Oct, 2023

What is Quartile Deviation?

Quartile Deviation (absolute measure) divides the distribution into multiple quarters. Quartile Deviation is calculated as the average of the difference of the upper quartile (Q₃) and the lower quartile (Q₁).

$Quartile~Deviation=\frac{Q_3-Q_1}{2}$

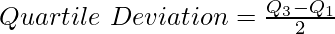
Where,

Q₃ = Upper Quartile (Size of $3[\frac{N+1}{4}]^{th}$ item)

Q₁ = Lower Quartile (Size of $[\frac{N+1}{4}]^{th}$ item)

What is Interquartile Range?
Interquartile Range refers to the difference between two quartiles.

Interquartile Range = Q₃– Q₁

What is Coefficient of Quartile Deviation?

For comparative studies of the variability of two or more series with different units, the Coefficient of Quartile Deviation (relative measure) is used.

$Coefficient~of~Quartile~Deviation=\frac{Q_3-Q_1}{Q_3+Q_1}$

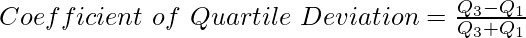
Where,

Q₃ = Upper Quartile (Size of $3[\frac{N+1}{4}]^{th}$ item)

Q₁ = Lower Quartile (Size of $[\frac{N+1}{4}]^{th}$ item)

Examples of Quartile Deviation in Continuous Series

Example 1:

Calculate the interquartile range, quartile deviation, and coefficient of quartile deviation from the following figures:

Solution:

$Q_1=Size~of~[\frac{N}{4}]^{th}~item=Size~of~[\frac{200}{4}]^{th}~item=Size~of~50^{th}~item$

Q₁ lies in the group 10-15.

l₁ = 10, c.f. = 24, f = 30, i = 5

$Q_1=l_1+\frac{\frac{N}{4}-c.f.}{f}\times i$

$Q_1=10+\frac{\frac{200}{4}-24}{30}\times 5$

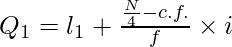
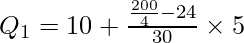
Q₁ = 14.33

$Q_3=Size~of~[\frac{3N}{4}]^{th}~item=Size~of~(\frac{3\times200}{4})^{th}~item=Size~of~150^{th}~item$

Q₃ lies in the group 20-25.

l₁ = 20, c.f. = 100, f = 60, i = 5

$Q_3=l_1+\frac{\frac{3N}{4}-c.f.}{f}\times i$

$Q_3=20+\frac{\frac{3\times200}{4}-100}{60}\times 5$

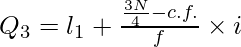
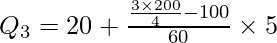
Q₃ = 24.16

Interquartile Range = Q₃ – Q₁ = 24.16 – 14.33 = 9.83

Quartile Deviation = 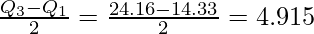$\frac{Q_3-Q_1}{2}=\frac{24.16-14.33}{2}=4.915$

Coefficient of Quartile Deviation = 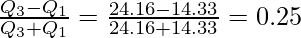$\frac{Q_3-Q_1}{Q_3+Q_1}=\frac{24.16-14.33}{24.16+14.33}=0.25$

Example 2:

Calculate the interquartile range, quartile deviation, and coefficient of quartile deviation from the following figures:

Solution:

$Q_1=Size~of~[\frac{N}{4}]^{th}~item=Size~of~[\frac{80}{4}]^{th}~item=Size~of~20^{th}~item$

Q₁ lies in the group 20-30.

l₁ = 20, c.f. = 14, f = 20, i = 10

$Q_1=l_1+\frac{\frac{N}{4}-c.f.}{f}\times i$

$Q_1=20+\frac{\frac{80}{4}-14}{20}\times 10$

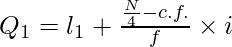
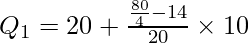
Q₁ = 23

$Q_3=Size~of~[\frac{3N}{4}]^{th}~item=Size~of~(\frac{3\times80}{4})^{th}~item=Size~of~60^{th}~item$

Q₃ lies in the group 30-40.

l₁ = 30, c.f. = 34, f = 28, i = 10

$Q_3=l_1+\frac{\frac{3N}{4}-c.f.}{f}\times i$

$Q_3=30+\frac{\frac{3\times80}{4}-34}{28}\times 10$

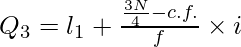
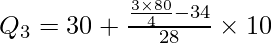
Q₃ = 39.28

Interquartile Range = Q₃ – Q₁ = 39.28 – 23 = 16.28

Quartile Deviation = 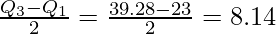$\frac{Q_3-Q_1}{2}=\frac{39.28-23}{2}=8.14$

Coefficient of Quartile Deviation = 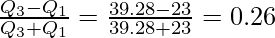$\frac{Q_3-Q_1}{Q_3+Q_1}=\frac{39.28-23}{39.28+23}=0.26$

Example 3:

Calculate the interquartile range, quartile deviation, and coefficient of quartile deviation from the following figures:

Solution:

$Q_1=Size~of~[\frac{N}{4}]^{th}~item=Size~of~[\frac{23}{4}]^{th}~item=Size~of~5.75^{th}~item$

Q₁ lies in the group 10-20.

l₁ = 10, c.f. = 4, f = 3, i = 10

$Q_1=l_1+\frac{\frac{N}{4}-c.f.}{f}\times i$

$Q_1=10+\frac{\frac{23}{4}-4}{3}\times 10$

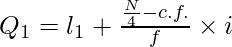
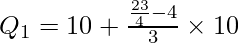
Q₁= 15.83

$Q_3=Size~of~[\frac{3N}{4}]^{th}~item=Size~of~(\frac{3\times23}{4})^{th}~item=Size~of~17.25^{th}~item$

Q₃ lies in the group 40-50.

l₁ = 40, c.f. = 13, f = 8, i = 10

$Q_3=l_1+\frac{\frac{3N}{4}-c.f.}{f}\times i$

$Q_3=40+\frac{\frac{3\times23}{4}-13}{8}\times 10$

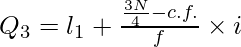
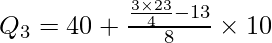
Q₃ = 45.31

Interquartile Range = Q₃ – Q₁ = 45.31 – 15.83 = 29.48

Quartile Deviation = 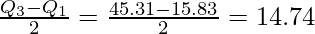$\frac{Q_3-Q_1}{2}=\frac{45.31-15.83}{2}=14.74$

Coefficient of Quartile Deviation = 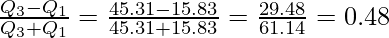$\frac{Q_3-Q_1}{Q_3+Q_1}=\frac{45.31-15.83}{45.31+15.83}=\frac{29.48}{61.14}=0.48$

Example 4:

Calculate the interquartile range, quartile deviation, and coefficient of quartile deviation from the following figures:

Solution:

$Q_1=Size~of~[\frac{N}{4}]^{th}~item=Size~of~[\frac{16}{4}]^{th}~item=Size~of~4^{th}~item$

Q₁ lies in the group 8.5-13.5.

l₁ = 8.5, c.f. = 3, f = 4, i = 5

$Q_1=l_1+\frac{\frac{N}{4}-c.f.}{f}\times i$

$Q_1=8.5+\frac{\frac{16}{4}-3}{4}\times 5$

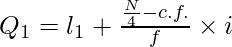
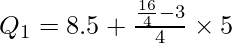
Q₁ = 9.75

$Q_3=Size~of~[\frac{3N}{4}]^{th}~item=Size~of~(\frac{3\times16}{4})^{th}~item=Size~of~12^{th}~item$

Q₃ lies in the group 18.5-23.5.

l₁ = 18.5, c.f. = 10, f = 2, i = 5

$Q_3=l_1+\frac{\frac{3N}{4}-c.f.}{f}\times i$

$Q_3=18.5+\frac{\frac{3\times16}{4}-10}{2}\times 5$

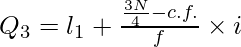
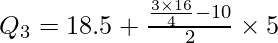
Q₃ = 23.5

Interquartile Range = Q₃ – Q₁ = 23.5 – 9.75 = 13.75

Quartile Deviation = 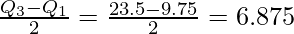$\frac{Q_3-Q_1}{2}=\frac{23.5-9.75}{2}=6.875$

Coefficient of Quartile Deviation = 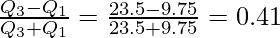$\frac{Q_3-Q_1}{Q_3+Q_1}=\frac{23.5-9.75}{23.5+9.75}=0.41$

Suggest improvement

Quartile Deviation in Discrete Series | Formula, Calculation and Examples

Mean Deviation: Coefficient of Mean Deviation, Merits, and Demerits

Share your thoughts in the comments

Chapter 1: Concept of Economics and Significance of Statistics in Economics

Chapter 2: Collection of Data

Chapter 3: Organisation of Data

Chapter 4: Presentation of Data: Textual and Tabular

Chapter 5: Diagrammatic Presentation of Data

Chapter 6: Measures of Central Tendency: Arithmetic Mean

Chapter 7: Measures of Central Tendency: Median and Mode

Chapter 8: Measures of Dispersion

Chapter 9: Correlation

Chapter 10: Index Number

Important Formulas in Statistics for Economics

Quartile Deviation in Continuous Series | Formula, Calculation and Examples

What is Quartile Deviation?

What is Interquartile Range?

What is Coefficient of Quartile Deviation?

Examples of Quartile Deviation in Continuous Series

Example 1:

Solution:

Example 2:

Solution:

Example 3:

Solution:

Example 4:

Solution:

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?